算法之二分查找(python&java版)

二分查找

基本原理

二分查找用于在一组排序好的数据中，查找某一个数据

我们以 [2,7,11,15,16，18,20]为例

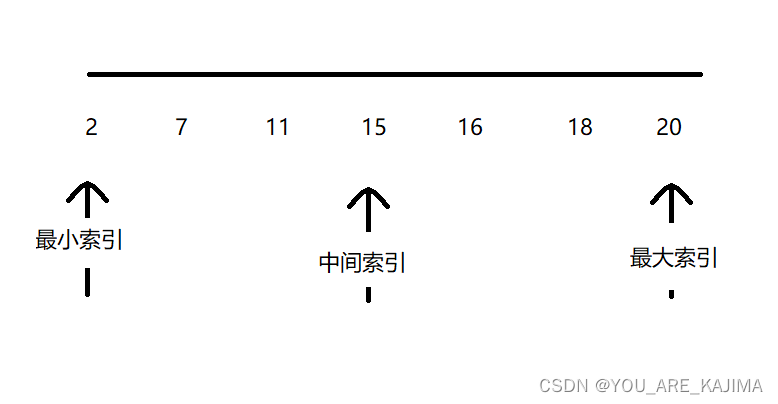
具体做法是：比如我们要查找7

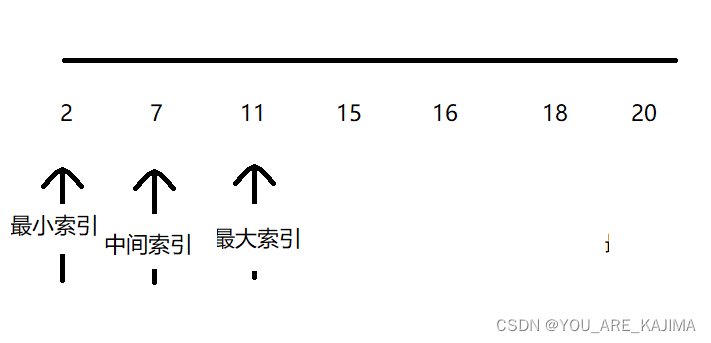
• 首先把7与中间索引的值作比较，7<15，然后把最大索引移到中间索引-1的位置上，也就是11上，这样中间位置的索引就变成了7的位置上
  

• 然后我们就行将7与中间索引位置的值比较，7=7，这样就得到了7，然后我们输出7所在位置的索引值即可

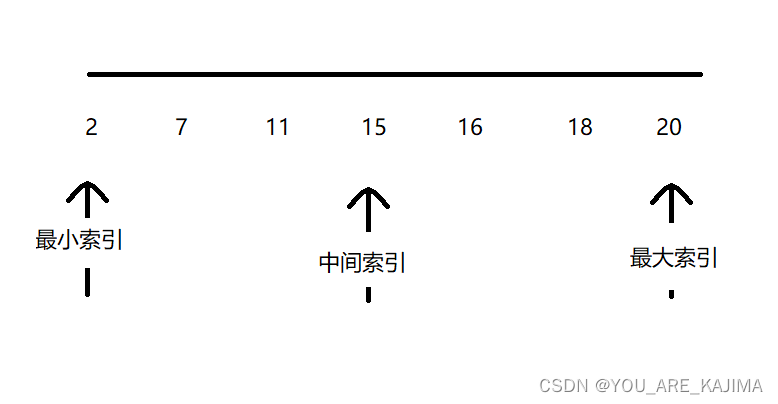
当然，如果我们要查找的数是16

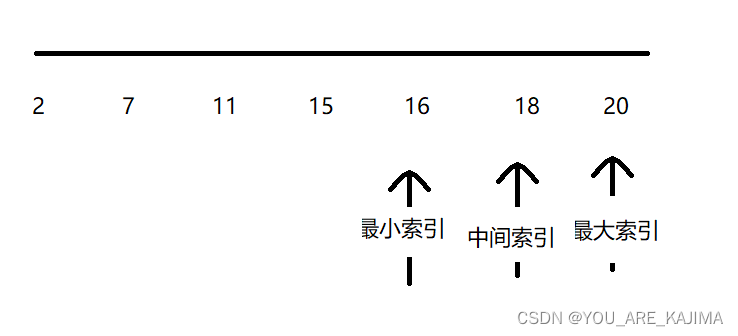
• 那我们就把15与16比较，15<16，我们就把最小索引移到中间索引+1的位置上，也就是16上，这样中间位置的索引就变成了18的位置上
  

• 然后我们再将要查找的16与中间索引的值比较，16<18，我们就把最大索引移到中间索引-1的位置上，也就是16上，这样中间索引也变成了16的位置那里
  

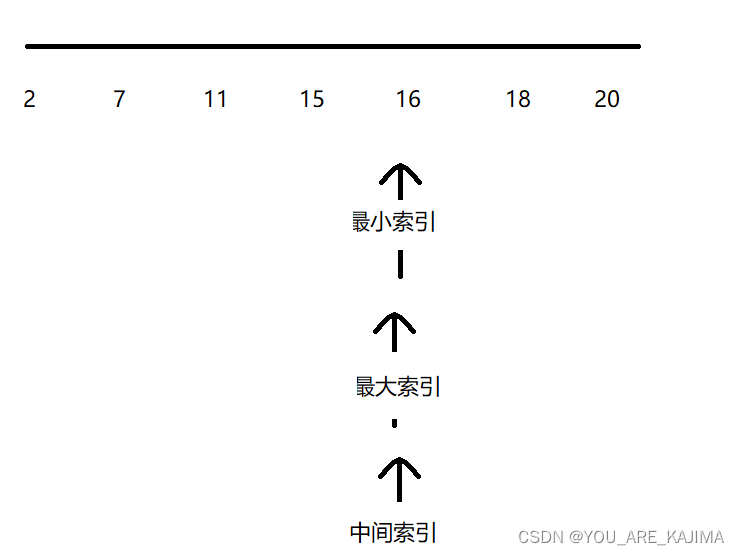
这样最小索引等于了最大索引，我们就得到了我们要查找的值，当然，在编程中，如果数组的个数是偶数个的，那中间位置的索引就会在取整的那个数上，比如有6个数，[1,2,3,4,5,6]，那中间索引的位置就会在3上面

编程实验

java篇

public static void main(String[] args) {
    int[] nums = {2,7,11,15,16,18,20};
    int num = 11;       //要查找的数
    int minIndex = 0;   //最小索引
    int maxIndex = nums.length-1; //最大索引
    int centerIndex = (minIndex+maxIndex)/2; //中间索引
    while(true) {
        //二分查找
        if (num > nums[centerIndex]) {  //如果要查找的数大于中间索引位置的值
            minIndex = centerIndex + 1; //将最小索引移动到中间索引位置+1
        } else if (num < nums[centerIndex]) { //如果要查找的数小于中间索引位置的值
            maxIndex = centerIndex - 1;   //将最大索引移动到中间索引位置-1
        } else{                           //如果要查找的数就等于中间索引位置的数直接输出中间索引
            System.out.println(centerIndex);
            break;
        }
        if(minIndex>maxIndex){         //如果最小索引大于最大索引就说明没找到
            System.out.println(-1);   //找不到输出-1
            break;
        }
        centerIndex = (minIndex+maxIndex)/2; //更新中间索引的位置
    }
}

python篇

nums=[2,7,11,15,16,18,20]
num = 11      # 要查找的数
minIndex = 0   # 最小索引
maxIndex = len(nums)-1 # 最大索引
centerIndex = int((minIndex+maxIndex)/2) # 中间索引
while 1:
    if num > nums[centerIndex]:   # 如果要查找的数大于中间索引位置的值
        minIndex = centerIndex + 1 # 将最小索引移动到中间索引位置+1
    elif num < nums[centerIndex]: # 如果要查找的数小于中间索引位置的值
        maxIndex = centerIndex - 1   # 将最大索引移动到中间索引位置-1
    else:                          # 如果要查找的数就等于中间索引位置的数直接输出中间索引
        print(centerIndex)
        break
    if(minIndex>maxIndex):       # 如果最小索引大于最大索引就说明没找到
        print(-1)   # 找不到输出-1
        break
    centerIndex = int((minIndex+maxIndex)/2) # 更新中间索引的位置