算法设计与分析——使用回溯法实现0-1背包问题——回溯法的基本回顾

问题描述

• 题目描述：
  有4个物品，其重量分别是{2, 3, 4, 5}，价值分别为{3, 4, 5, 6}，背包的容量为8。如何装才能价值最大，最大价值为多少？

• 输入格式：
  第一行：是测试数据。
  接下来对于每组测试数据，第一行是物品数量和背包最大承重，第二行是每个物品的价值，第三行是每个物品的重量。

• 输出格式：
  一个整数，为最大价值总和是多少。

• 输入样例：

    4 8
    3 4 5 6
    2 3 4 5
  

• 输出样例：

    10
  

回溯算法的回顾

• 概述：回溯算法是一种通用的解题法，有较广的适用性
• 基本步骤：
  • 定义问题的解空间，解空间必须包括问题的最优解，一般情况下要列出所有的解
  • 确定易于搜索的解空间结构：常用的有两种，子集树（零一背包问题）和排列树（货郎问题）
    * 子集树：从n个元素的集合S中找出满足某种性质的子集时
    * 排列树：从n个元素的集合S中找出满足某种性质的排列时
  • 从根节点出发，以深度优先的方式去搜索解空间树
  • 确定剪枝函数，两种策略：约束函数和限界函数

使用知识回顾去解决问题

定义问题的解空间

• 解空间必须包含的问题的最优解的
• 一般情况下，都是列出所有的解
  

确定易于搜索的解空间结构

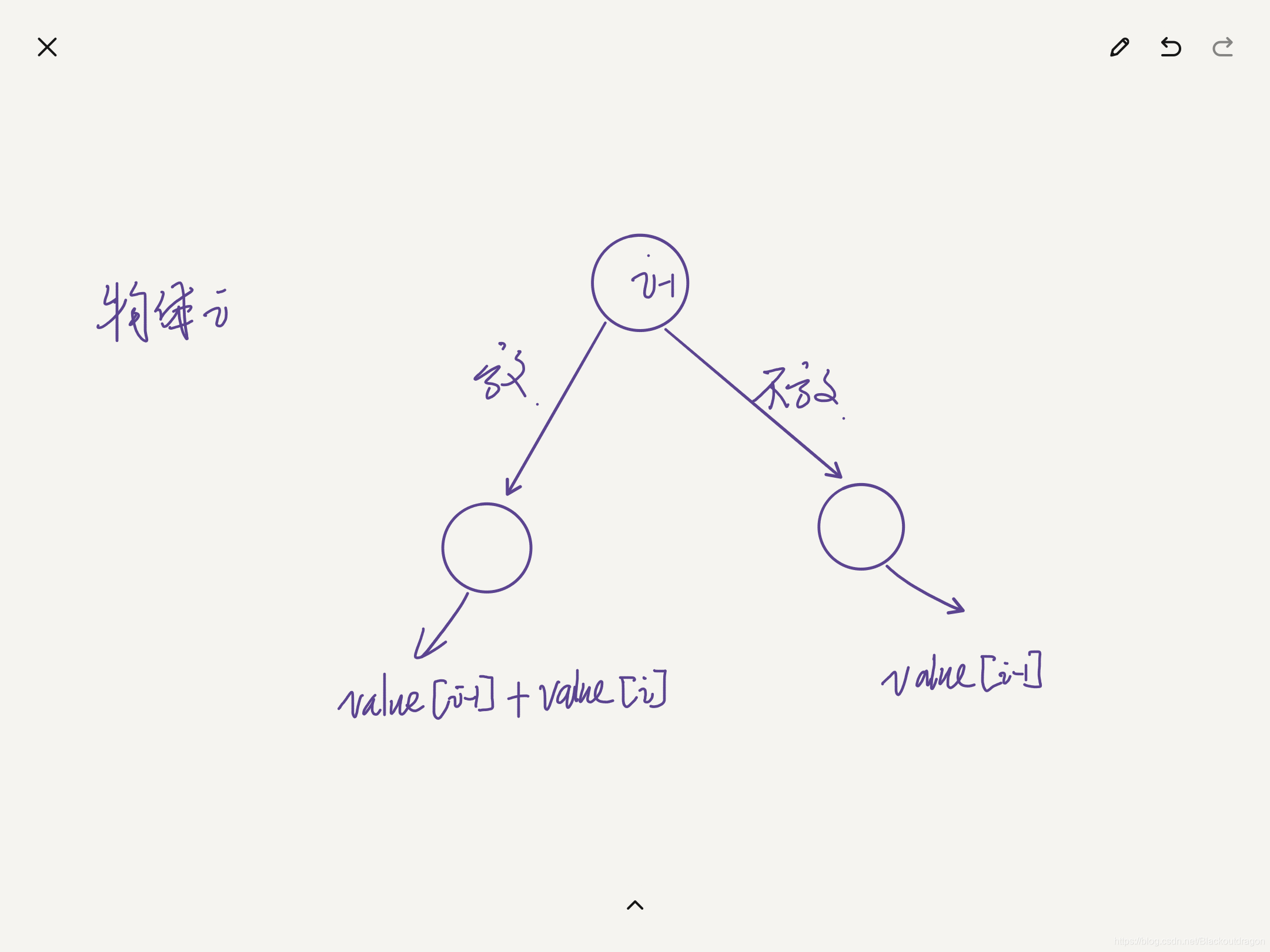
• 定义问题的解空间，每一个物品有两种状态，放或者不放，形成对应的树形结构如图。

单个物体

多个物体

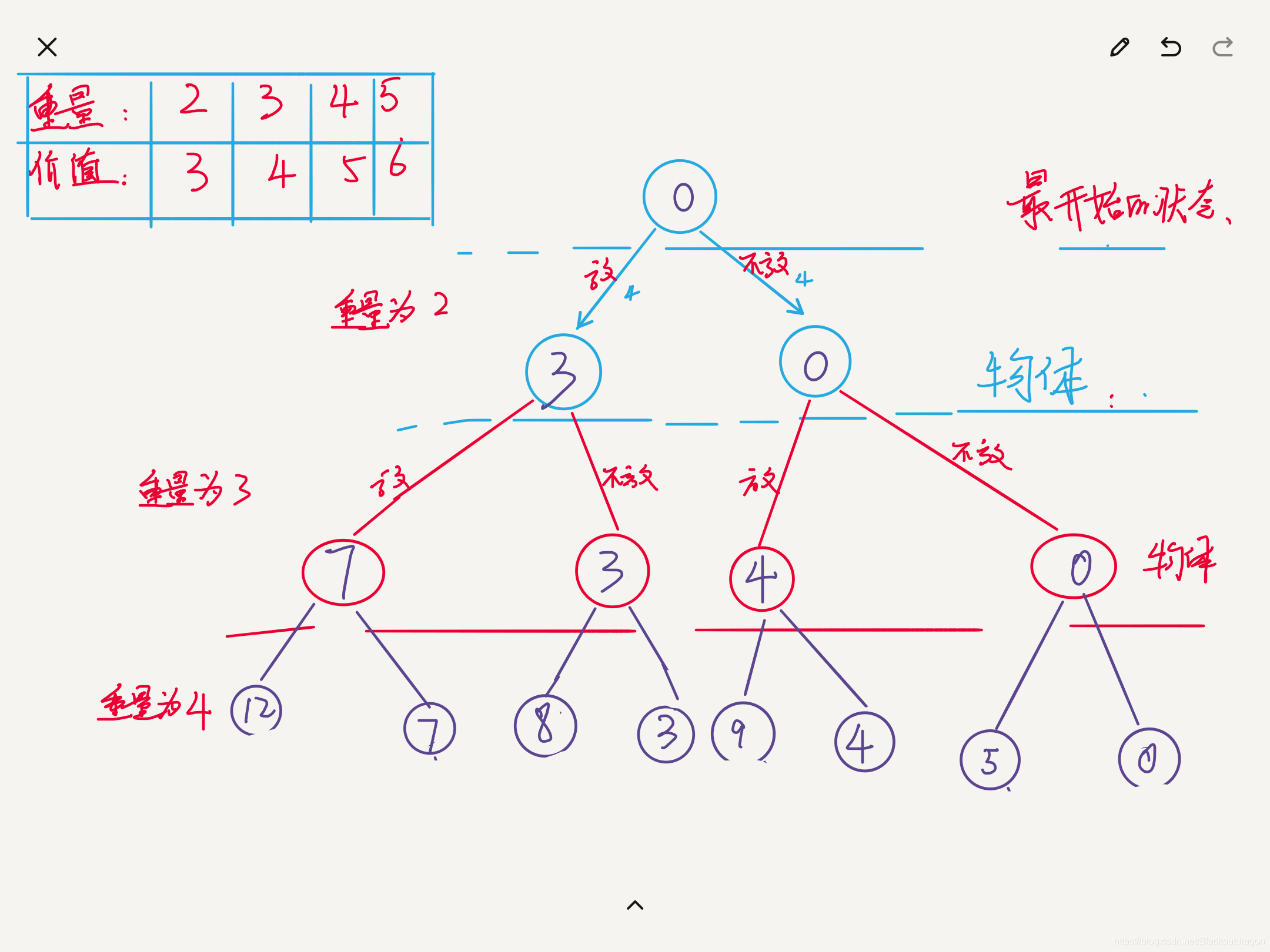
• 因为每一个物体只有放或者不放两种状态，就是一个二叉树，这里只列了三层，实际上有四层，每一个结点的值是当前物体的价值。
• 其实，我知道表示成了二叉树，但是并不知道如何使用代码去实现。使用二叉树的数据结构吗？链表还是数组。

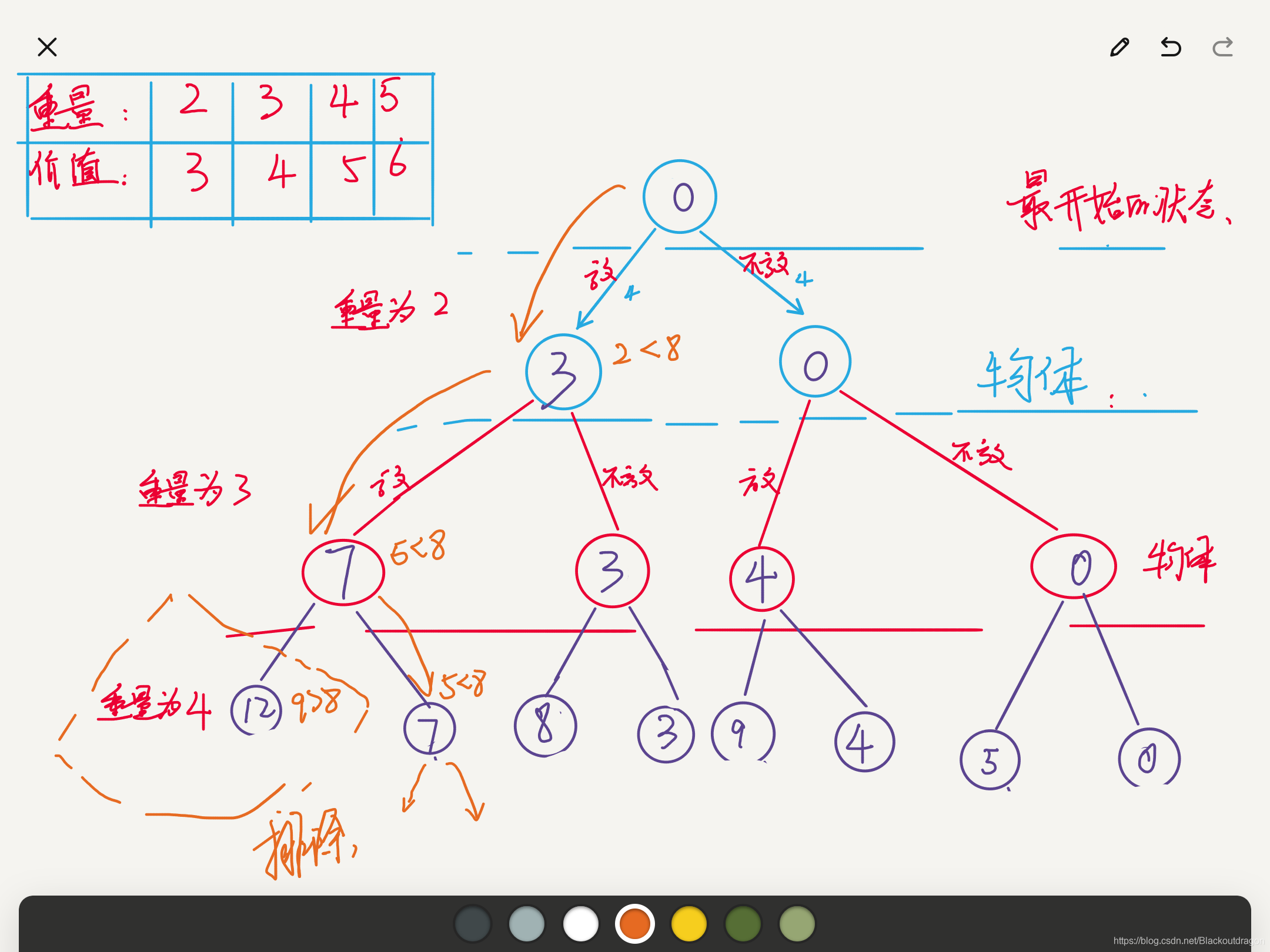
从根节点出发以深度优先的方式搜索空间树

• 从根节点出发以深度优先的方式搜索解空间树。算法搜索至空间树的任意一点时，先判断该点是否包含问题的解。
• 判断依据：
  * 肯定不包含解，即重量超过背包的容量，则跳过对该节点为根的子树的搜索，逐层向祖先结点回溯
  * 肯定包含解，即重量没有超过背包的容量，则继续按照深度优先搜索的策略进行搜索。
  

实现代码

#include<iostream>
#include<math.h>

using namespace std;

//用于记录是否存放当前地物体
int inOut[4];
//保存最多的价值
int value;
//定义背包的总共的重量的
int bagVolume = 9;

/*
	描述：背包问题的约束条件，当传入对应的序号，就去判定是否要放对应的物品
	参数：放入包中物体的序号
	返回：当前物体总重量和背包容量的关系
		 true：表示没有超重
		 false：表示超重
	原理：判定当前的物品的总重量，是不是小于物体的实际重量
*/
bool bagConstraint(int m, int weight[]) {
	//一直遍历m层之前的所有物体，求出其对应的重量
	int allweight = 0;
	for (int i = 0; i <= m; ++i)
	{
		//计算出总共的重量的
		allweight += inOut[i] * weight[i];
	}

	//比较当前的物体总重量和背包的总重量关系
	return allweight <= bagVolume;
}

/*
	描述：深度优先搜索的函数，递归函数
	参数：m:是要装入背包的物品的数量
		 weight：是背包中各个物品的重量
		 value：是背包中各个物品的价值
	返回：最终返回的是最大的价值
	问题：
*/
void bagProblem(int m, int weight[], int valueAll[]) {

	//首先确定终止条件，那就比较最大值
	if (m == 4)
	{
		int sum = 0;
		for (int i = 0; i < m; ++i)
		{
			sum += valueAll[i] * inOut[i];
		}

		//比较最大值
		if (sum > value)
		{
			value = sum;
		}
	}
	else {
		//没有到达终止条件，继续向下进行递归
		for (int i = 0; i < 2; ++i)
		{
			inOut[m] = i;
			//判定是否满足对应约束条件
			if (bagConstraint(m, weight))
			{
				//满足约束条件，继续向下进行递归的
				bagProblem(m + 1, weight, valueAll);
			}
		}

	}

}

int main(int argc, char const* argv[])
{
	cout << "输入的样例：物品数量：4" << endl;
	cout << "背包容量：9" << endl;
	cout << "重量分别是：2 3 4 5" << endl;
	cout << "价值分别是：3 4 5 6 " << endl;
	int num = 4;
	int weight[4] = { 2,3,4,5 };
	int valueAll[4] = { 3,4,5,6 };
	bagProblem(0, weight, valueAll);
	cout << "最终的结果是：" << value << endl;
	cout << endl;
	return 0;

}