线代——猴博士笔记
求向量组的秩,先求极大无关组,极大无关组里几个向量,秩就是几
什么是极大无关组?从一向量组挑出几个向量,他们线性无关,且原来向量组中任意一个向量加进去,又变成了相关的。
什么是线性相关?对于一向量组,存在 不全为0的实数k1-km 使得这些数与每个向量相乘的和 = 0
- 行列式=0,线性相关
- 一向量组的子集线性相关,整体线性相关
计算行列式
公式1:

公式2:
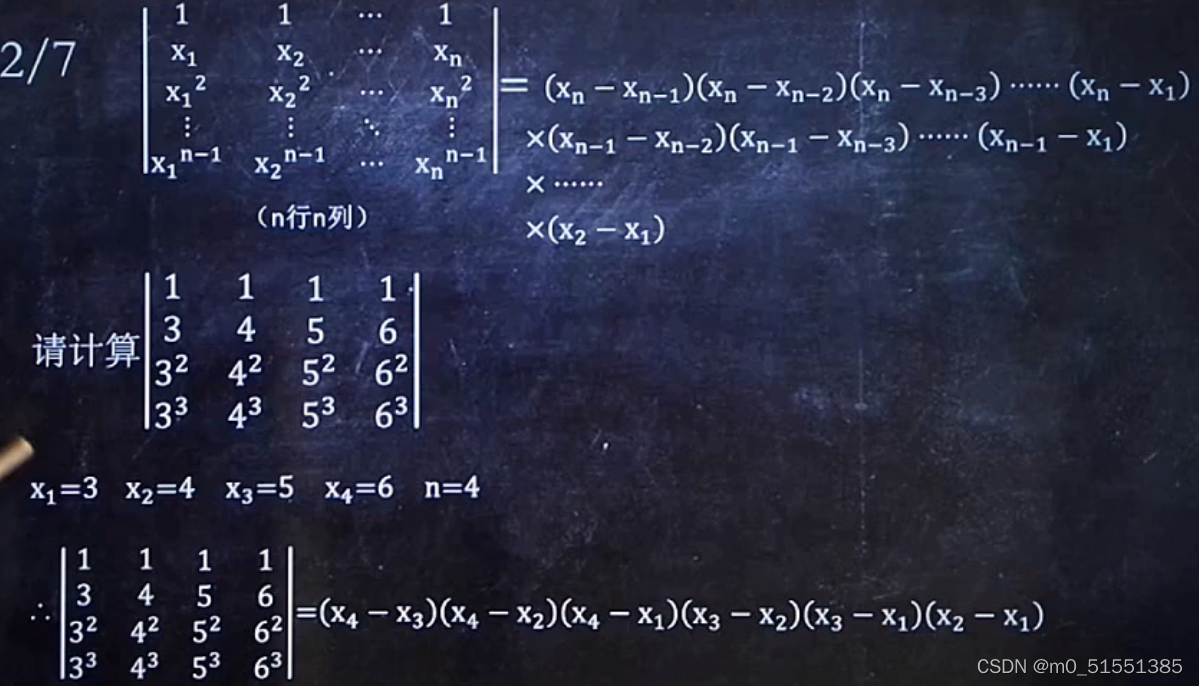
公式3:

两行(列)交换,行列式值变相反数
公式4:求余子式 和 代数余子式
公式5:
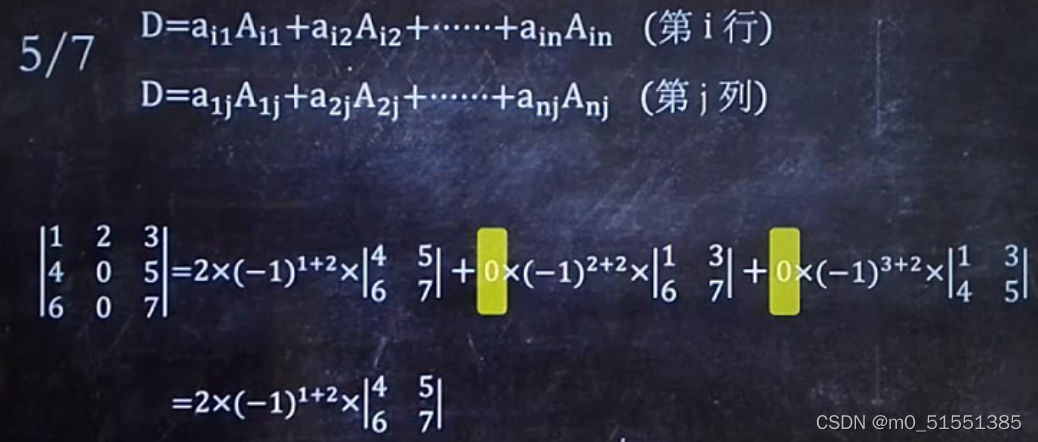
公式6:


公式7:
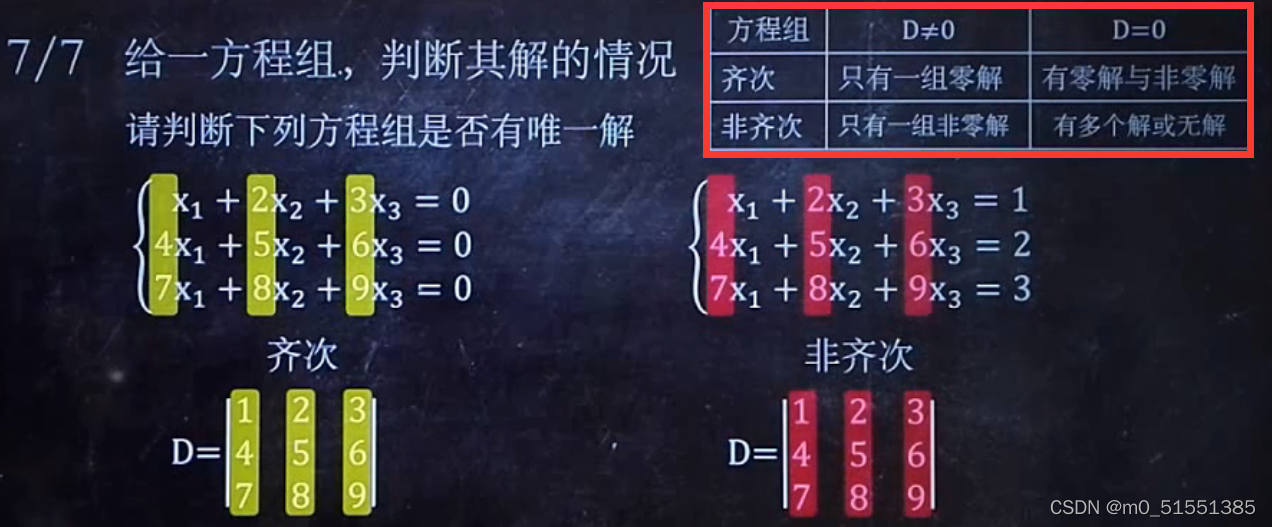

矩阵


转置矩阵性质

有可逆矩阵的条件:


 先从上往下做,再从下往上做,就能得到单位矩阵
先从上往下做,再从下往上做,就能得到单位矩阵
可逆矩阵:
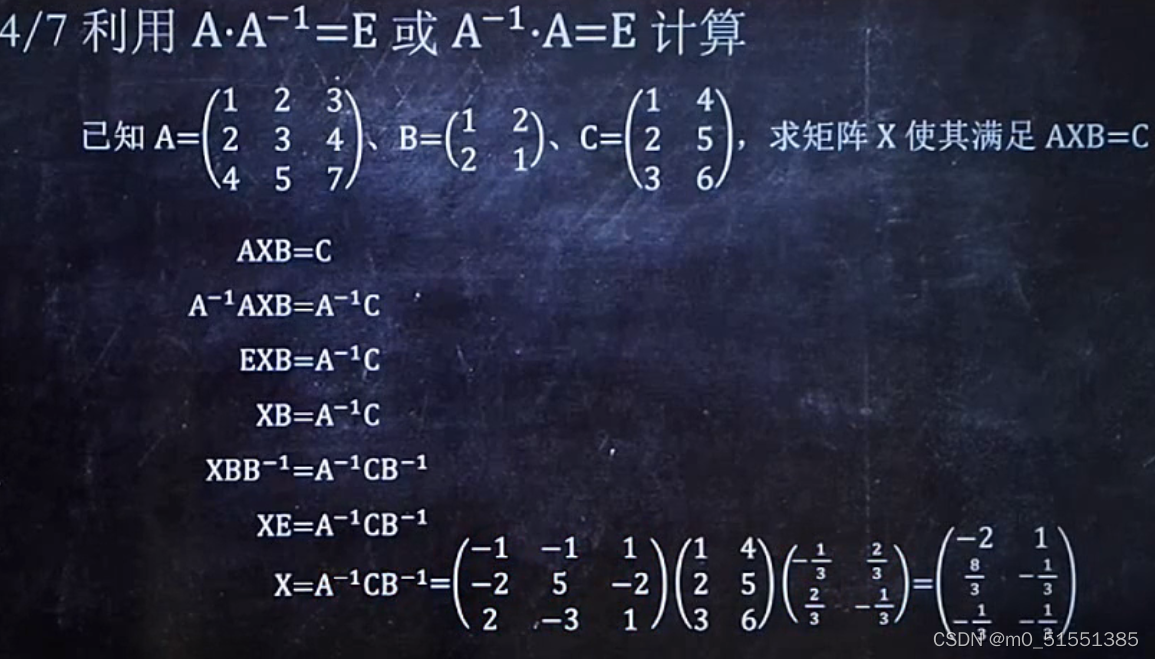

乘一个A,把A* 消掉

在阶梯型矩阵中,几行有非0数,秩就是几
矩阵乘一个满秩矩阵,秩不变

判断:判断秩相等

判断线性相关无关:比较秩 和 向量个数

题型:

注意这里是求 行 向量的极大无关组,列向量不能这么求
(极大无关组 = 极大线性无关组)

判断方程组的解的情况:

齐次无解例题:

非齐次无解例题:

==========================================================================
解方程组:共有五步
求增广矩阵的秩:

变换矩阵:
R=3,就变换前三行,前三列,为单位矩阵的形式

根据②得到的矩阵变回方程组:

设未知数:

整理成标准型,再用刚刚设的未知数替代题目原来的未知数:

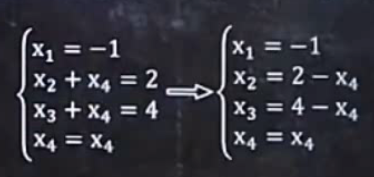
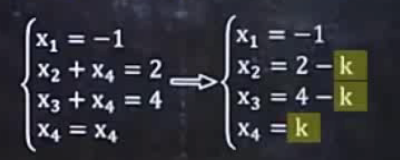
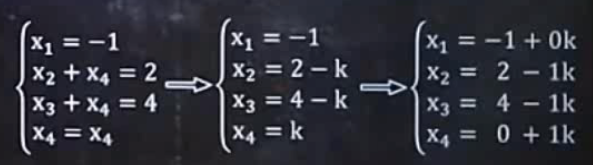
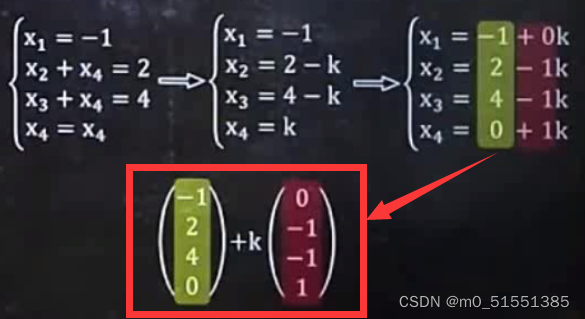
下面就是本题的解,k可取任意值:
例题练习:

如果是齐次方程组呢?
常数项都抹掉就完了、

==========================================================================
求方程组的通解、特解。基础解系:
要先解出方程组的解。
通解,含有所有的未知数,能代表所有情况的解

特解就是一组x1–xn的值,代入原方程,可以满足:
也就是未知数随便取值:这是一个特解

这也是一个特解:一般都令所有未知数=0

基础解系:

==========================================================================
已知方程组多个特解,求某齐次方程组的通解:
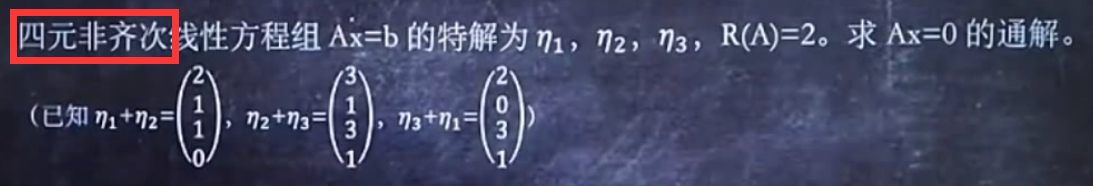
共三步:
一设未知数:

二:
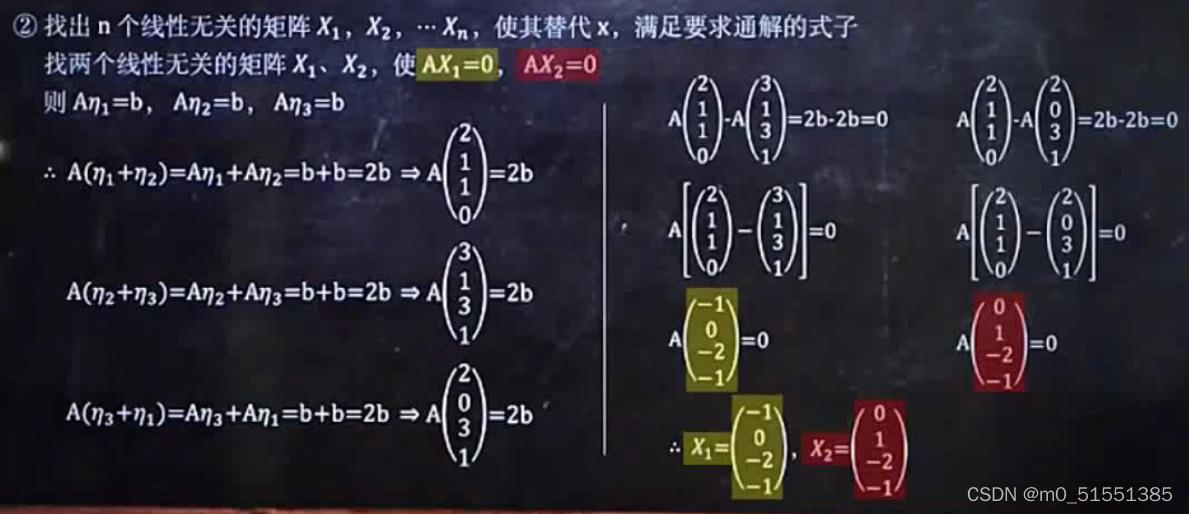
三:
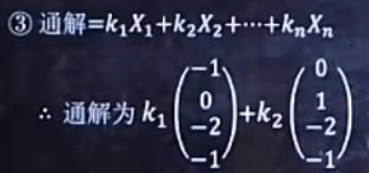
==========================================================================
已知某方程组多个特解,求某非齐次方程组的通解:
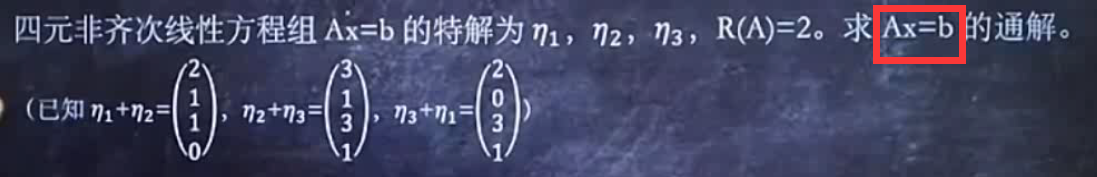
共四步。
一设未知数:
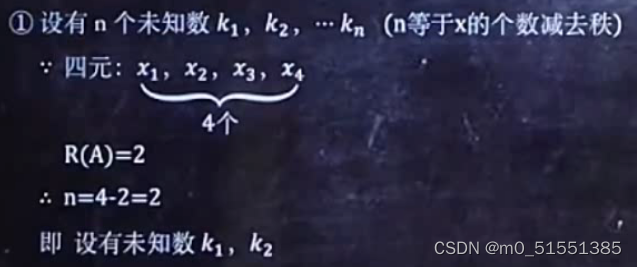
二:

三:

四:
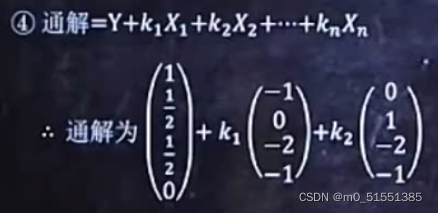
==========================================================================
判断解集合中线性无关的解向量的个数:
直接背公式:
齐次:

非齐次:

==========================================================================
方阵对角化及其应用:
规范正交化:
中括号:
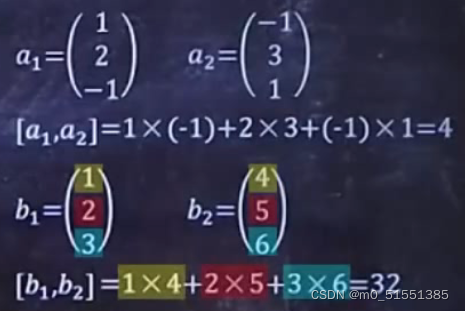
双竖线||:
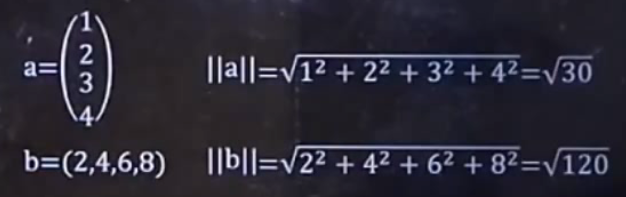
纯带公式:最后的e就是结果

==========================================================================
求矩阵特征值:
λ的数量一定 = 方阵的阶数

矩阵特征值 与 行列式的关系:

==========================================================================
求矩阵的特征向量:
把上面求出来的特征值带到(A-λE)里得出一个矩阵,矩阵转化成方程组,求通解:
通解里面有两项,求出来的是两个特征向量:

例题:

==========================================================================
判断方阵是否与对角阵相似或满足某式子:
(题外话:任意两矩阵相似,他们的 特征值,秩,行列式,主对角线元素之和 都相同)



求对角阵 及 可逆变换矩阵:

分五步:
一:求特征值,特征向量

二:写出对角阵

三:去掉特征向量中的k
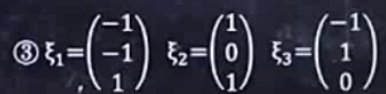
四:规范正交化:
操作规则:


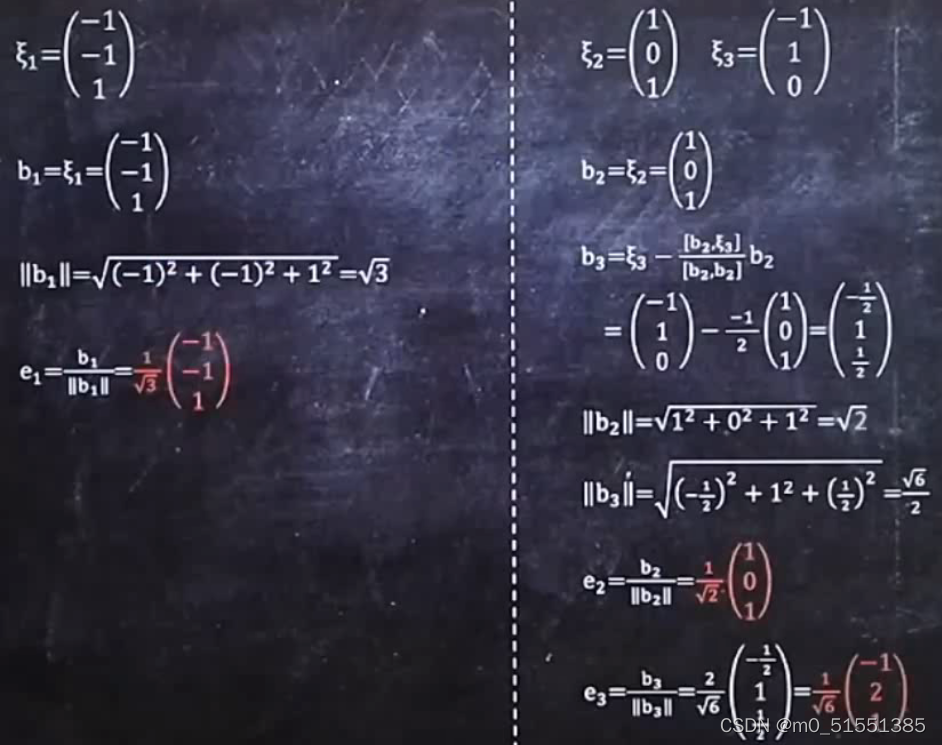
五:排列上述正交化后的向量,得出可逆变换矩阵:

==========================================================================
P是可逆变换矩阵

==========================================================================
==========================================================================
二次型:
求二次型对应的 系数矩阵(对称阵):
公式:
注意公式的第一行,没有系数2,第二行往后的a都×了2
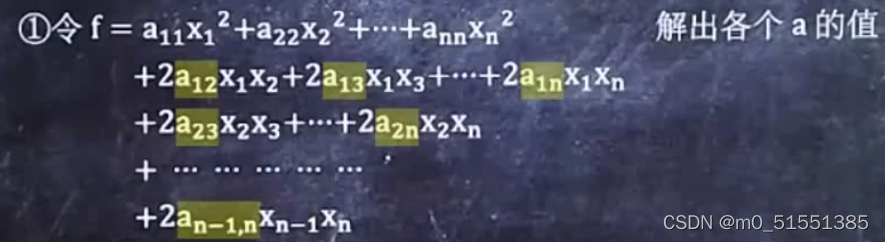
例题:


==========================================================================
二次型化成标准型:
这俩都是一个题型
一:求系数矩阵A
二:求A的特征值
三:根据公式就能求出 标准型
四:根据上一节,求可逆变换矩阵

==========================================================================
二次型化成规范性:
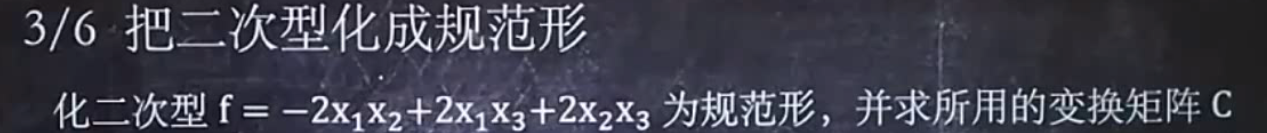
一:求稀系数矩阵
二:求系数矩阵特征值
三:写出规范型
四:求可逆变换矩阵
五:求出变换矩阵,(可逆变换矩阵再×一个矩阵)

==========================================================================
配方法化二次型为标准型:
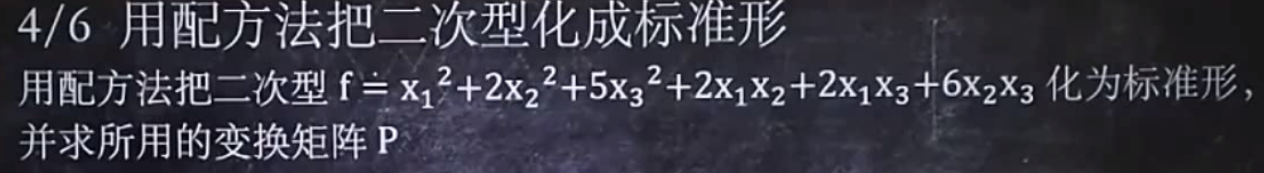
一:配方

==========================================================================
判断二次型的正定性:
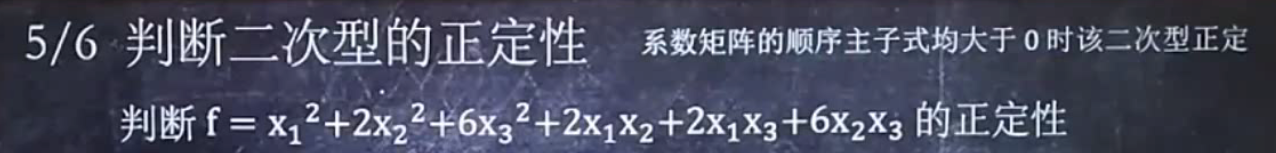
一:求出系数矩阵
二:写出所有顺序主子式,并计算行列式的值是否>0

==========================================================================
二次型(或者说任意一个矩阵)为正定的等价条件:
下面这几个条件对于任意矩阵也成立
