区间型动态规划——最长回文子序列

给定一个字符串 s ，找到其中最长的回文子序列，并返回该序列的长度。可以假设 s 的最大长度为 1000 。

示例 1:

一个可能的最长回文子序列为 “bbbb”。

输入:
"bbbab"
输出:
4

一个可能的最长回文子序列为 “bbbb”。

1、题目分析

这个题目可以划分为序列类型的动态规划，也可以划作为区间类型的动态规划。就我个人的思想而言，更接近区间类型的动态规划。

2、确定状态

最优策略产生最长的回文子串T，长度是M

• 情况1：回文串长度是1，即一个字母

• 情况2：回文串长度大于1，那么必定有T[0]=T[M-1]

设T[0]是S[i], T[M-1]是S[j] ，T剩下的部分T[1…M-2]仍然是一个回文串，而且是S[i+1…j-1]的最长回文子串

因此我们可以假设状态f[i][j]为S[i……j]的最长回文子串的长度。

3、转移方程

假设状态f[i][j]为S[i……j]的最长回文子串的长度

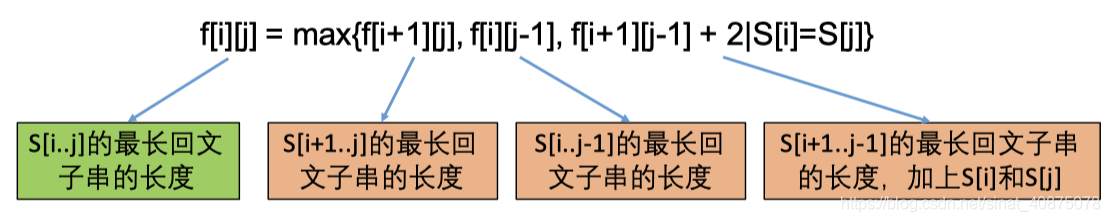
4、初始条件和边界情况

初始条件

– f[0][0] = f[1][1] = … = f[N-1][N-1] = 1

• 一个字母也是一个长度为1的回文串

– 如果S[i] == S[i+1], f[i][i+1] = 2

– 如果S[i] != S[i+1], f[i][i+1] = 1

5、计算顺序

这种类型的题目比较特殊，不能逐行去计算，需要按照j-i从小到大的顺序去计算

答案是f[0][N-1]。

时间复杂度O(N*N)，空间复杂度O(N*N)

6、代码实现

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        if len(s) == 0:
            return 0
        n = len(s)
        dp = [[0] * n for i in range(n)]
        for i in range(n):
            dp[i][i]=1
        for i in range(n-1,-1,-1):
            for j in range(i+1,n):
                if s[i]==s[j]:
                    dp[i][j] = max(dp[i][j], dp[i+1][j-1] + 2)
                else:
                    dp[i][j]=max(dp[i+1][j],dp[i][j-1])
        return dp[0][n - 1]