Burg法求解AR(p)模型参数(一)自回归模型
文章目录
第一章 自回归模型
第一节 概念
一、自回归模型
1.1 定义
在许多应用中,时序数据Xt通常可由历史数据的加权和与随机扰动的叠加来表示,如公式(1)中所示
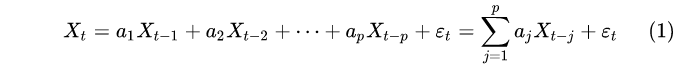
其中a1为常系数, ε t为随机扰动(噪声)项。自回归(Autoregression)模型即是这样一种采用式(1)描述时序数据的时间序列模型。
1.2 自回归模型的平稳解
所谓平稳解,即是满足式(1)的平稳时间序列。需要指出的是,式(1)不一定存在平稳解。在实际应用中,一般假设 ε t为 高斯白噪声WN(0,σ2 )。在这种情况下,平稳解总是存在的。
二、推移算子
2.1 概念
对任何时间序列 {Xt}和无穷级数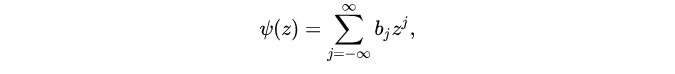
只要级数
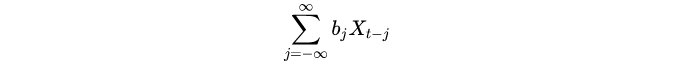
在某种意义下收敛(例如 a.s.收敛,依概率收敛,均方收敛),就定义
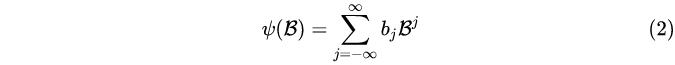
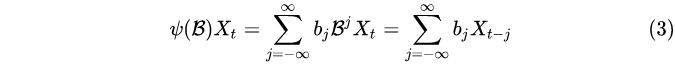
并称B是时间t的向后推移算子,简称推移算子,且BjXt = Xt-j 。
2.2 性质
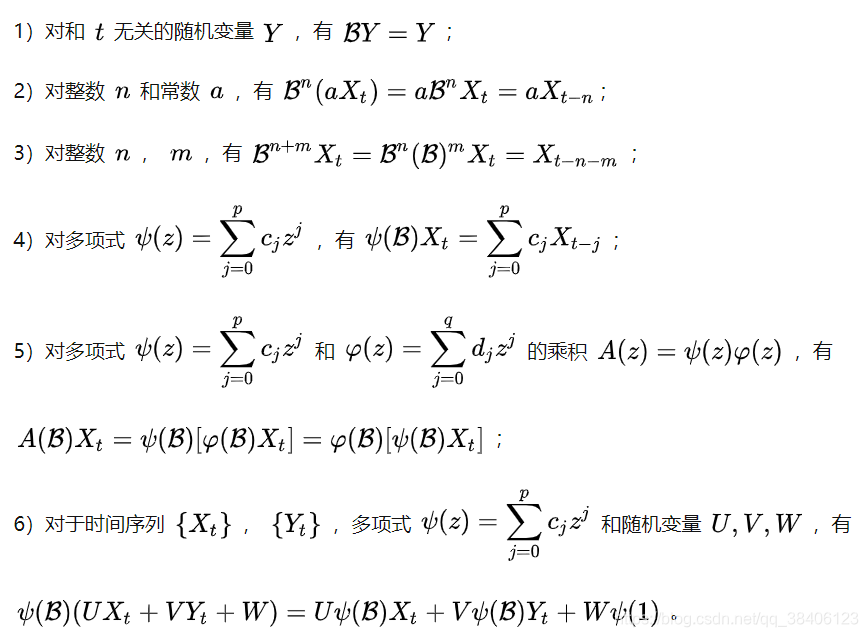
三、A(z)
3.1 概念
给定 p 个实数a 1,a 2,a 3……a p ,(a p≠0),称
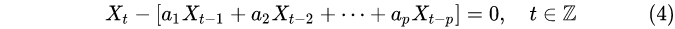
为 p 阶齐次常系数线性差分方程,简称为齐次差分方程。满足式(4)的时间序列称为齐次差分方程(4)的解。
注:在数学上,递推关系(recurrence relation),也就是差分方程(difference equation),是一种递推地定义一个序列的方程式:序列的每一项目是定义为前一项的函数。
可以看出,式(4)的解可以由它的p 个初值 X 0,X 1,X 2……X p-1 逐步递推得到,
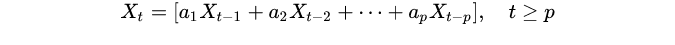
所以{X t}可以由这 p 个初值唯一决定。因为初值是可以任意选择的,所以式(4)的解有无穷多个。
利用推移算子B,可以把式(4)写成等价形式,
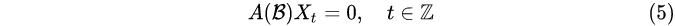
其中
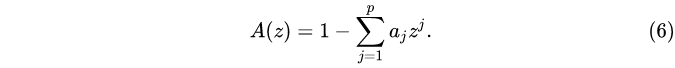
A(z)称为式(4)的特征多项式。
3.2 性质
1)如果多项式A(z)的根都在单位圆外,即 |zj|>1 ,那么 {Xt}以负指数阶收敛到零;
2)如果多项式 A(z)在单位圆内有根,即 |zj|≤1 ,那么差分方程(4)存在发散的解。
四、AR(p)模型
一般情况下只考虑稳定的差分方程系统(更有应用价值),这就是著名的AR§ 模型。
4.1 定义
如果{ε t} 是白噪声 WN(0,σ2 ),实数a 1,a 2,a 3……a p(a p≠0)使得多项式 A(z) 的零点都在单位圆外:
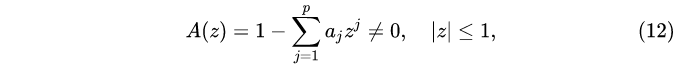
就称公式(13)是一个 p阶自回归模型,简称AR(p)模型。
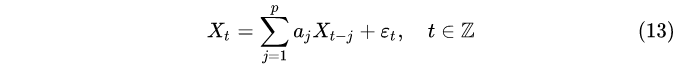
满足公式(13)的平稳时间序列 {Xt}称为平稳解或 AR§序列。称 a=(a 1,a 2,a 3……a p)T 是AR(p)模型的自回归系数。称公式(12)是稳定性条件或最小相位条件。
4.2 AR(p)模型的平稳解
利用时间推移算子可以将公式(13)改写成
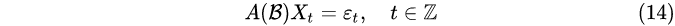
设多项式 A(z)的互异根是 z 1,z 2z 3……z k,则对 1<ρ<min{|zj|} , A-1(z)=1/A(z)是{z:|z|<ρ}内的解析函数。从而有Taylor级数
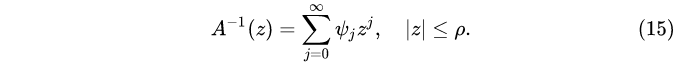
由级数(15)在z=ρ的绝对收敛性得到:当 j→∞时, |Ψj ρj|→0。于是由
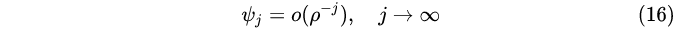
知道{Ψj}绝对可和。
定义
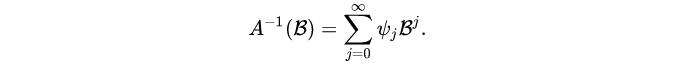
则由
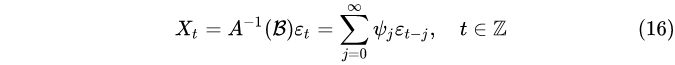
决定的平稳序列是AR(p)序列。式(16)中的系数称为平稳序列 {Xt}的Wold系数。
可以证明式(16)是AR(p)模型(13)的唯一平稳解。
4.3 AR(p)模型的通解
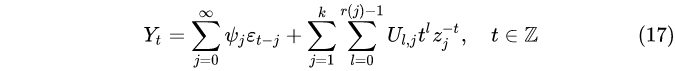
式中{Ul,j}为随机变量。
参考
1.自回归模型.