[编译原理-词法分析(三)] 词法分析器

前言

从构思到实现，试过语法分析树和抽象语法树，写起来不是特别顺利，然后换了思路，以一种直观的方式进行词法分析（可能时间复杂度较高，没计算过）。

项目地址

Github

参考链接

在实现的过程中也发掘到几篇不错的blog

构建抽象语法树
构建正则引擎
正则表达式转有限状态自动机

前文

支持语法

表达式	匹配	例子
c	单个非运算字符c	a, b, z
\c	字符c的字面值	\\
“s”	串s的字面值	".\“
.	除换行符以外的所有字符	*.out
[s]	字符串s中的任意一个字符	[abc], [a-z], [0-9]
[^s]	不在字符串s中的任意一个字符	[^abc]
r1r2	r1后加上r2	abc
（r）	与r相同	(ab)
r{m, n}	最少m个，最多n个r重复出现	r{1, 5}
r1 | r2	r1或r2	a | b
r*	和r匹配的零个或多个串连接的串	a*, [abc]*
r+	和r匹配的一个或多个串连接的串	a+, [0-9]+
r?	零个或一个r	a?, (ab)?

注解₁：c匹配的是非元标识字符, 即除(\ " . ^ …) 代表特定意义的字符。 \c 匹配的是元标识字符的字面值, 即 ‘.’ 匹配除换行符以外的字符, 加上 ‘\.’ 表示匹配一个小数点 ‘.’ 。

注解₂： r*口语为kleene闭包(克林闭包)，r+口语为正闭包，r?口语为???(我也不知道)。

注解₃：在上个版本中支持[^s]，但由于在当前版本改动了规则的继承层次，导致无法直接实现此功能（或许有方法，笑）。

注解₄：构建 ‘.’ 元标识符时，会有bug（绘制出NFA就明白了）。

注解₅：在当前版本中，没有构建符号表，因为算是测试版本，返回的Token的实例也很‘直接’。

注解₆：在当前版本中，有正则表达式到不确定有穷自动机的转换；不确定的有穷自动机 转 确定的有穷自动机没办法实现，需要一点小改动才可。子集构造法的三个函数有，转换类也有（注解了），在正文部分会提及如何。

正文

语法分析树，抽象语法树 ，规则与定式

什么是有限状态自动机?
|
​ 有限状态自动机是一个五元组
$$M=(Q,\Sigma ,\delta ,q0,F)$$
$Q$ 状态的非空有穷集合，$\forall q\in Q$，$q$称为$M$的一个状态
$\Sigma$ 输入字母表
$\delta$ 状态转移函数，有时又叫作状态转换函数，$\delta ：Q\times \Sigma \to Q，\delta (q,a)=p$
$q0$ $M$的开始状态，也可叫作初始状态或启动状态，$q0\in Q$
$F$ $M$的终止状态集合，$F$被$Q$包含，任给$q\in F$，$q$称为$M$的终止状态

简要提及：
正则表达式（Regular Expression， RE）
不确定的有限状态自动机（Nondeterministic Finite Automata，NFA）
确定的有限状态自动机（Deterministic Finite Automata，DFA）

1. 规则

每个规则类都包含输入字母表中的一个子集，即$R\in \Sigma$；
每个状态通过匹配规则到达新的状态，即$\delta (q_1,R)=q_2$；

说起来比较抽象，其实很容易理解：
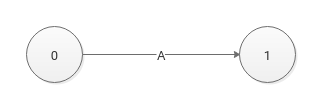例如图一，0号状态可以通过单字符规则（CharacterRule）到达1号状态

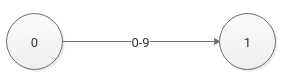
在图二中，0号状态可以通过或规则（OrRule），即0~9中任意一个字符可以到达1号状态。
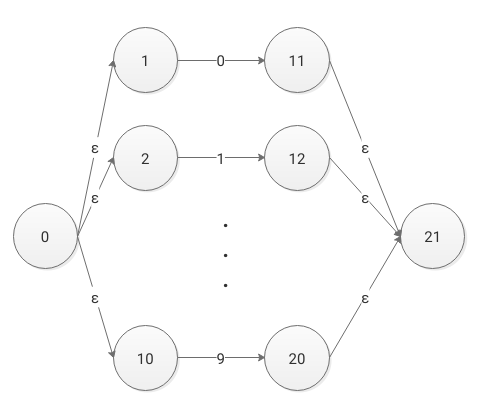
图二是图三的简化版（防止状态数过多），虽然状态数减少，但是在某些时候就不是特别适用了，例如需要转换为确定的有穷自动机时，我们知道子集构造法中move函数接受的是单字符（详情见代码 SubsetConstruction类），而简化版本用的是ConjunctionSymRule（连词符规则），导致不能够精确匹配，也就不能转换为确定的有穷自动机。

2. 定式

为了生成有限状态自动机的方便，每个规则可以生成一个模板有限状态自动机，称之为定式。像$r\ast$，$r+$，$r?$这三种闭包都有固定的NFA模板，得到r直接生成即可，即：RE -> NFA

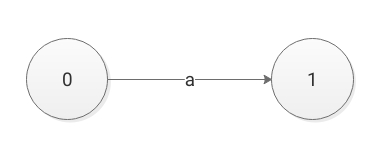
图四的正则式为: $r->a$，构建一个单定式有限状态自动机，0号状态即Start State，1号状态即Accept State。

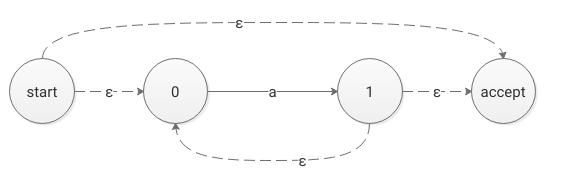
为图四构建一个Kleene闭包，即 r * 。

由规则生成的有限状态自动机，此自动机包含一个开始状态和一个接受状态，不用考虑在开始状态和接受状态之间有多少转换。

3. 代码

讲完了在项目中最主要的两项-规则与定式，其他不是那么重要，包括输入文件，双缓冲区方案等等。

输入文件: 正则定义文件 和 识别源文件

上面是此次正则定义中的一部分，每行都包含一个正则表达式以及该正则表达式的名称，形式为：
$$name\to RE$$

如果某个正则表达式A需要使用其他正则表达式B，则B必须在A之前声明(如digit和number的关系)

识别源文件是正则定义所能表示的语言。

输出形式：返回识别源中的每个词素，即正则定义中每个正则表达式能匹配识别源文件中的的最小单位。

输出中的一部分：

规则与定式类图

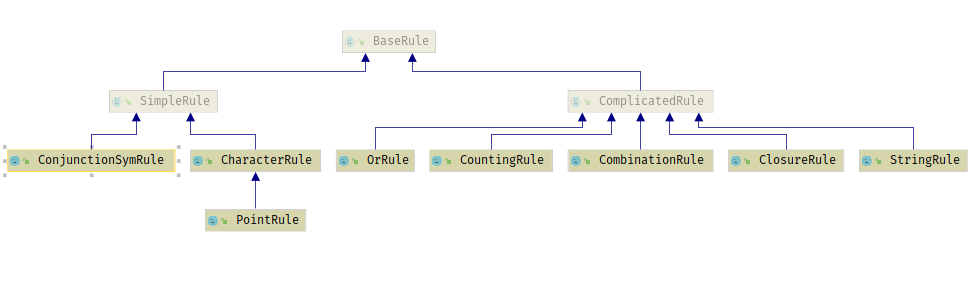
1. 所有类将继承BaseRule，BaseRule有一个生成状态图（有限状态自动机）的方法
2. BaseRule有两个子类，SimpleRule和ComplicatedRule；在这里的意为：ComplicatedRule第二次生成的自动机是第一次生成的自动机的拷贝（未实现…），SimpleRule每次生成的自动机都是重新实例的。
3. 下面有七个实际规则：
   单字符规则（CharacterRule），通过字符C可由当前状态到新的状态；
   字符串（StringRule），一个单字符规则序列；
   连词符规则（ConjunctionSymRule），连词符是类似[a-z]、[0-9]中的-符号，表示a₁,a₂,a₃…a_n,形成一个逻辑上连续的序列时，可以表示为a₁-a_n。
   或规则（OrRule），包含一个规则序列，只要匹配其中任意一个即可到达新的状态。
   计数规则 （CountingRule）正则式 r { m , n } r\{m, n\} r{m,n}的规则实例。
   闭包规则 （ClosureRule）由一个基础规则和一个闭包属性组成。
   组合规则（CombinationRule）是一个规则序列，匹配时需要按照顺序匹配。
   4.PointRule是CharacterRule的一个特化，不算实际规则。

在其中，字符串规则不是必要规则，只是为了简化状态数所用规则。（在用连接定式时，两个正则式之间需要插入一条空转换函数，如果类似 double -> double 这条正则式，每个字符构成的单字符规则，在连接时需要插入五个空转换函数，将多出五个无用状态。）

!!!
在当前版本中，SimpleRule还包含一个match方法，即有限状态机上的一个转换函数，所有继承SimpleRule的类才可调用匹配方法。

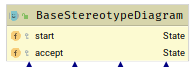
1. 所有定式都继承自BaseStereotypeDiagram，每个定式状态图包含一个开始状态和接受状态，不用考虑在开始状态和接受状态之间有多少转换。

2. 还有一个比较特殊的抽象基类，BaseClosureStereotypeDiagram，所有闭包类都继承此类。

3. 一共三种基础定式和三种闭包定式：
   SingleStereotypeState 构建 $$\begin{gathered} c, \\ c,0-9 \end{gathered}$$(图二连词符规则也是一条单定式)
   OrStereotypeState 构建 $[a-z]$
   ConnectStereotypeState 构建$ r₁r₂， r { m , n } r\{m, n\} r{m,n}

   KleeneClosureState 构建 $r\ast$
   PositiveClosureState 构建 $r+$
   ZeroOneClosureState 构建 $r?$

特殊类

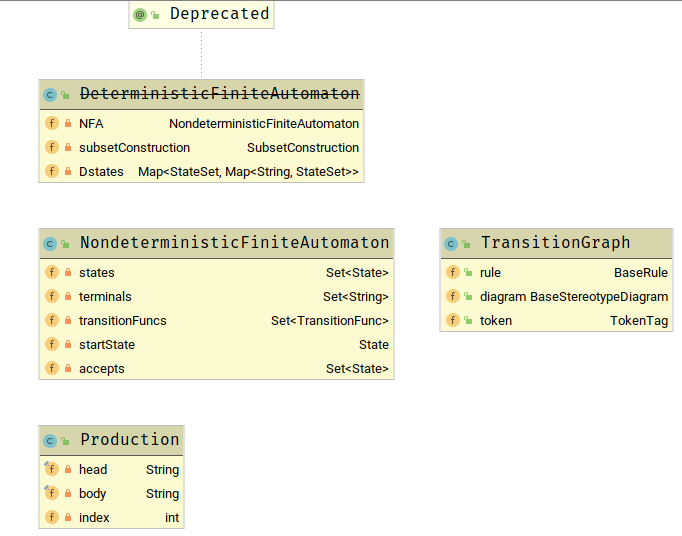Production意为产生式，即一条正则表达式和该正则表达式的名称，产生式的叫法是在文法中称呼的，即有：
$$head\to body$$
head称为产生式头部或产生式左部，body称为产生式体或产生式右部。
TransitionGraph存放一条规则和一张转换表，一行正则表达式对应一个TransitionGraph实例。

DeterministicFiniteAutomaton是指DFA，因为未实现，所以注解了。

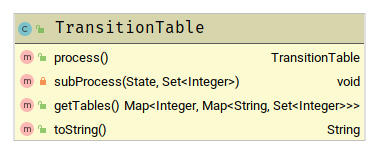
传入一个NFA 生成一张转换表

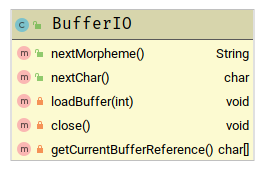
双缓冲区方案，比之另外一个早期实现的C++要稍好（笑）
双缓冲区blog c++实现

后记

整个项目写得挺一般的，代码约2k，功能不算特别完备，bug也挺多（前文那里列出了）。至于为什么写，是在学编译原理的时候想找份代码瞧瞧词法分析是怎么回事（龙书有前端代码demo），可是网上找不到呀!! 然后就写了一份；可优化的地方还有几处，如果以后有时间或许会更新，谢谢！

标签

正则表达式，RE，有穷状态自动机，DFA，NFA
正则表达式转不确定的有限状态自动机
词法分析 JAVA实现