递归树法求解递归式

 递归算法时间复杂度的计算方程式一个递归方程：

　　

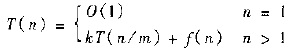
　　在引入递归树之前可以考虑一个例子：

　　T(n) = 2T(n/2) + n2

　　迭代2次可以得：

　　T(n) = n2 + 2(2T(n/4) + (n/2) 2)

　　还可以继续迭代，将其完全展开可得：

　　T(n) = n2 + 2((n/2) 2 + 2((n/22)2 + 2((n/23) 2 + 2((n/24) 2 +…+2((n/2i) 2 + 2T(n/2i + 1)))…))))　　……(1)

　　而当n/2i+1 == 1时，迭代结束。

 

　　将(1)式小括号展开，可得：

　　T(n) = n2 + 2(n/2)2 + 22(n/22) 2 + … + 2i(n/2i)2 + 2i+1T(n/2i+1)

　　这恰好是一个树形结构，由此可引出递归树法。

 

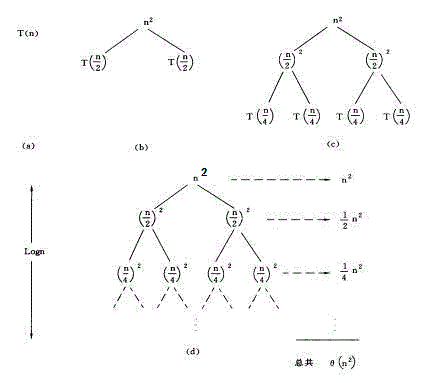
　　图中的(a)(b)(c)(d)分别是递归树生成的第1,2,3,n步。每一节点中都将当前的自由项n2留在其中，而将两个递归项T(n/2) + T(n/2)分别摊给了他的两个子节点，如此循环。

　　图中所有节点之和为:

　　[1 + 1/2 + (1/2)2 + (1/2)3 + … + (1/2)i] n2 = 2n2

　　可知其时间复杂度为O(n2)

　　

　　可以得到递归树的规则为：

　　(1) 每层的节点为T(n) = kT(n / m) + f(n)中的f(n)在当前的n/m下的值；

　　(2) 每个节点的分支数为k；

　　(3)每层的右侧标出当前层中所有节点的和。

 

　　再举个例子：

　　T(n) = T(n/3) + T(2n/3) + n

　　其递归树如下图所示：

　　

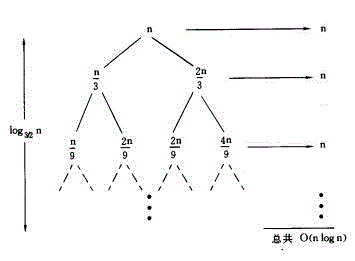
　　可见每层的值都为n，从根到叶节点的最长路径是：

　　

　　因为最后递归的停止是在(2/3)kn == 1.则

　　　　　　

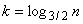
　　于是

　　　　

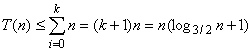
　　即T(n) = O(nlogn)　

 

　　总结，利用此方法解递归算法复杂度：

　　f(n) = af(n/b) + d(n)

　　1.当d(n)为常数时：

　　

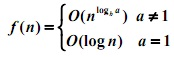
　　2.当d(n) = cn 时：

 　　

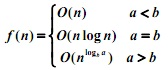
　　3.当d(n)为其他情况时可用递归树进行分析。

 

主定理

下面给出主方法所依赖的定理。

定理4.1（主定理） 令 a≥1 和 b>1 是常数，f(n) 是一个函数，T(n) 是定义在非负整数上的递归式：
T(n) = aT(n/b) + f(n)
那么T(n)有如下渐进界：

1. 若对某个常数 ε>0 有 f(n) = O(nlogba-ε)，则 T(n) = Θ(nlogba) 。
2. 若 f(n) = Θ(nlogba)，则 T(n) = Θ(nlogba lgn) 。
3. 若对某个常数 ε>0 有 f(n) = Ω(nlogba+ε)，且对某个常数 c<1 和所有足够大的 n 有 af(n/b) ≤ cf(n)，则 T(n) = Θ(f(n)) 。

作者：金戈大王
链接：https://www.jianshu.com/p/4d0b005782d9
来源：简书
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

　　

　　由第二种情况知，若采用分治法对原算法进行改进，则着重点是采用新的计算方法缩小a值。　

          原文链接http://www.cnblogs.com/wu8685/archive/2010/12/21/1912347.html