二叉树的创建以及基础遍历算法（c++）

一、二叉树的创建

1.树结构定义

二叉树是树结构的一种特殊结构，每一个节点最多有左孩子和右孩子两个子节点。所以在定义树结构的时候可以定义根节点ID、左右子节点的ID、以及指向左右子节点的指针。定义如下：

class TreeNode
{
public:
	TreeNode* m_pLeftChild, * m_pRightChild;
	int m_nRootId;       //根节点ID
	int m_nLeftId;      //子孩子节点ID
	int m_nRightId;     //右孩子节点ID
	int m_nChildCount;  //子孩子个数
};

2. 二叉树的创建

给定一组数据，在创建的二叉树的时候按照左节点小于根节点，右节点大于根节点的原则进行创建，下面一组数据创建的二叉树结构应如图所示。
int data[9] = { 6, 7, 2, 9, 3, 1, 8, 2, 4 };​

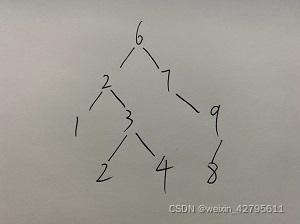
创建逻辑如下：

TreeNode *BinaryTree::CreateNode(int data)
{
	TreeNode* node = new TreeNode;
	node->m_nRootId = data;
	node->m_pLeftChild = NULL; 
	node->m_pRightChild = NULL;
	node->m_nChildCount = 0;
	node->m_nLeftId = NULL;
	node->m_nRightId = NULL;

	return node;
}

void BinaryTree::InsertNode(int data)
{
	TreeNode* node = CreateNode(data);

	if (m_pTreeNode == NULL) {
		m_pTreeNode = node;
	}
	else {
		TreeNode* pChild = m_pTreeNode;
		
		while (pChild != NULL) {
			if (pChild->m_nRootId > data) {            //小于就进左儿子
				if (pChild->m_pLeftChild == NULL) {
					pChild->m_pLeftChild = node;
					pChild->m_nLeftId = data;
					pChild->m_nChildCount++;
					return;
				}
				else {
					pChild = pChild->m_pLeftChild;
					
				}	
			}
			else {
				if (pChild->m_pRightChild == NULL) {
					pChild->m_pRightChild = node;
					pChild->m_nRightId = data;
					pChild->m_nChildCount++;
					return;
				}
				else {
					pChild = pChild->m_pRightChild;
					
				}
			}
		}
	}
}

二、二叉树的遍历

二叉树的遍历分为深度优先遍历和广度优先遍历，其中深度优先遍历分为前序遍历、中序遍历和后序遍历；广度优先则是对每一层进行遍历；

深度遍历：

前序遍历：根左右。先打印，再遍历左子树，再遍历右子树；
中序遍历：左根右。先遍历左子树，再打印，再遍历右子树；
后序遍历：左右根。先遍历左子树，再遍历右子树，再打印。
深度优先遍历可以用递归算法和非递归算法实现

1. 递归遍历

1）前序遍历

void BinaryTree::PreorderTraversal(TreeNode *node)
{
	if (node == NULL)
		return;

	cout << node->m_nRootId << " ";

	PreorderTraversal(node->m_pLeftChild);
	PreorderTraversal(node->m_pRightChild);
}

2）中序遍历

void BinaryTree::InorderTraversal(TreeNode* node)
{
	if (node == NULL)
		return;

	InorderTraversal(node->m_pLeftChild);

	cout << node->m_nRootId << " ";

	InorderTraversal(node->m_pRightChild);
}

3）后序遍历

void BinaryTree::PostSequenceTraversal(TreeNode* node)
{
	if (node == NULL)
		return;

	PostSequenceTraversal(node->m_pLeftChild);
	PostSequenceTraversal(node->m_pRightChild);

	cout << node->m_nRootId << " ";
}

2. 非递归遍历

1）前序遍历

void BinaryTree::PreorderTraversal()
{
	if (m_pTreeNode == NULL)
		return;

	stack<TreeNode*> TreeStack;
	TreeNode* p = NULL;

	TreeStack.push(m_pTreeNode);
	while (!TreeStack.empty()) {
		p = TreeStack.top();
		TreeStack.pop();

		cout << p->m_nRootId << " ";
		if (p->m_pRightChild != NULL)
			TreeStack.push(p->m_pRightChild);
		if (p->m_pLeftChild != NULL)
			TreeStack.push(p->m_pLeftChild);
	}
}

2）中序遍历

void BinaryTree::InorderTraversal()
{
	if (m_pTreeNode == NULL)
		return;

	stack<TreeNode*> TreeStack;
	TreeNode* p = NULL;
	  
	TreeStack.push(m_pTreeNode);
	while (!TreeStack.empty()) {
		while ((p = TreeStack.top()) && p) {
			TreeStack.push(p->m_pLeftChild);  //将节点左孩子放入栈中
		}

		TreeStack.pop();
		if (!TreeStack.empty()) {
			p = TreeStack.top();
			TreeStack.pop();
			cout << p->m_nRootId << " ";
			TreeStack.push(p->m_pRightChild);	
		}
	}
}

3）后序遍历

void BinaryTree::PostSequenceTraversal()
{
	if (m_pTreeNode == NULL)
		return;

	stack<TreeNode*> TreeStack1, TreeStack2;
	TreeNode* p = NULL;

	TreeStack1.push(m_pTreeNode);
	while (!TreeStack1.empty()) {
		p = TreeStack1.top();
		TreeStack1.pop();
		TreeStack2.push(p);

		if (p->m_pLeftChild != NULL)
			TreeStack1.push(p->m_pLeftChild);
		if (p->m_pRightChild != NULL)
			TreeStack1.push(p->m_pRightChild);
	}

	while (!TreeStack2.empty()) {
		cout << TreeStack2.top()->m_nRootId << " ";
		TreeStack2.pop();
	}
}

4）广度优先遍历

void BinaryTree::levelOrderTraversal()
{
	if (m_pTreeNode == NULL)
		return;

	queue<TreeNode*> TreeStack;
	TreeNode* p = NULL;

	TreeStack.push(m_pTreeNode);
	while (!TreeStack.empty()) {
		p = TreeStack.front();
		TreeStack.pop();
		if (p->m_pLeftChild != NULL)
			TreeStack.push(p->m_pLeftChild);
		if (p->m_pRightChild != NULL)
			TreeStack.push(p->m_pRightChild);

		cout << p->m_nRootId << " ";
	}
}

三、完整代码

首先是BinaryTreeNode.h头文件

#pragma once
#include <vector>

using namespace std;

class TreeNode
{
public:
	TreeNode* m_pLeftChild, * m_pRightChild;
	int m_nRootId;       //根节点ID
	int m_nLeftId;      //子孩子节点ID
	int m_nRightId;     //右孩子节点ID
	int m_nChildCount;  //子孩子个数
};

class BinaryTree
{
public:
	BinaryTree();
	~BinaryTree();
public:
	//生成二叉树
	void InsertNode(int data);


	/*递归算法*/
	//前序遍历
	void PreorderTraversal(TreeNode* node);
	//中序遍历
	void InorderTraversal(TreeNode* node);
	//后序遍历
	void PostSequenceTraversal(TreeNode* node);

	/*非递归算法*/
	void PreorderTraversal();
	void InorderTraversal();
	void PostSequenceTraversal();

	//广度优先遍历
	void levelOrderTraversal();
protected:
	TreeNode* CreateNode(int data);
public:
	TreeNode* m_pTreeNode;
};

下面是BinaryTreeNode.cpp文件

#include "BinaryTreeNode.h"
#include <iostream>
#include <stack>
#include <queue>

using namespace std;

BinaryTree::BinaryTree()
{
	m_pTreeNode = NULL;
}

BinaryTree::~BinaryTree()
{
	delete m_pTreeNode;
}

TreeNode *BinaryTree::CreateNode(int data)
{
	TreeNode* node = new TreeNode;
	node->m_nRootId = data;
	node->m_pLeftChild = NULL; 
	node->m_pRightChild = NULL;
	node->m_nChildCount = 0;
	node->m_nLeftId = NULL;
	node->m_nRightId = NULL;

	return node;
}

void BinaryTree::InsertNode(int data)
{
	TreeNode* node = CreateNode(data);

	if (m_pTreeNode == NULL) {
		m_pTreeNode = node;
	}
	else {
		TreeNode* pChild = m_pTreeNode;
		
		while (pChild != NULL) {
			if (pChild->m_nRootId > data) {            //小于就进左儿子
				if (pChild->m_pLeftChild == NULL) {
					pChild->m_pLeftChild = node;
					pChild->m_nLeftId = data;
					pChild->m_nChildCount++;
					return;
				}
				else {
					pChild = pChild->m_pLeftChild;
					
				}	
			}
			else {
				if (pChild->m_pRightChild == NULL) {
					pChild->m_pRightChild = node;
					pChild->m_nRightId = data;
					pChild->m_nChildCount++;
					return;
				}
				else {
					pChild = pChild->m_pRightChild;
					
				}
			}
		}
	}
}


void BinaryTree::PreorderTraversal(TreeNode *node)
{
	if (node == NULL)
		return;

	cout << node->m_nRootId << " ";

	PreorderTraversal(node->m_pLeftChild);
	PreorderTraversal(node->m_pRightChild);
}

void BinaryTree::InorderTraversal(TreeNode* node)
{
	if (node == NULL)
		return;

	InorderTraversal(node->m_pLeftChild);

	cout << node->m_nRootId << " ";

	InorderTraversal(node->m_pRightChild);
}

void BinaryTree::PostSequenceTraversal(TreeNode* node)
{
	if (node == NULL)
		return;

	PostSequenceTraversal(node->m_pLeftChild);
	PostSequenceTraversal(node->m_pRightChild);

	cout << node->m_nRootId << " ";
}

void BinaryTree::PreorderTraversal()
{
	if (m_pTreeNode == NULL)
		return;

	stack<TreeNode*> TreeStack;
	TreeNode* p = NULL;

	TreeStack.push(m_pTreeNode);
	while (!TreeStack.empty()) {
		p = TreeStack.top();
		TreeStack.pop();

		cout << p->m_nRootId << " ";
		if (p->m_pRightChild != NULL)
			TreeStack.push(p->m_pRightChild);
		if (p->m_pLeftChild != NULL)
			TreeStack.push(p->m_pLeftChild);
	}
}

void BinaryTree::InorderTraversal()
{
	if (m_pTreeNode == NULL)
		return;

	stack<TreeNode*> TreeStack;
	TreeNode* p = NULL;
	  
	TreeStack.push(m_pTreeNode);
	while (!TreeStack.empty()) {
		while ((p = TreeStack.top()) && p) {
			TreeStack.push(p->m_pLeftChild);  //将节点左孩子放入栈中
		}

		TreeStack.pop();
		if (!TreeStack.empty()) {
			p = TreeStack.top();
			TreeStack.pop();
			cout << p->m_nRootId << " ";
			TreeStack.push(p->m_pRightChild);	
		}
	}
}

void BinaryTree::PostSequenceTraversal()
{
	if (m_pTreeNode == NULL)
		return;

	stack<TreeNode*> TreeStack1, TreeStack2;
	TreeNode* p = NULL;

	TreeStack1.push(m_pTreeNode);
	while (!TreeStack1.empty()) {
		p = TreeStack1.top();
		TreeStack1.pop();
		TreeStack2.push(p);

		if (p->m_pLeftChild != NULL)
			TreeStack1.push(p->m_pLeftChild);
		if (p->m_pRightChild != NULL)
			TreeStack1.push(p->m_pRightChild);
	}

	while (!TreeStack2.empty()) {
		cout << TreeStack2.top()->m_nRootId << " ";
		TreeStack2.pop();
	}
}

//广度优先遍历
void BinaryTree::levelOrderTraversal()
{
	if (m_pTreeNode == NULL)
		return;

	queue<TreeNode*> TreeStack;
	TreeNode* p = NULL;

	TreeStack.push(m_pTreeNode);
	while (!TreeStack.empty()) {
		p = TreeStack.front();
		TreeStack.pop();
		if (p->m_pLeftChild != NULL)
			TreeStack.push(p->m_pLeftChild);
		if (p->m_pRightChild != NULL)
			TreeStack.push(p->m_pRightChild);

		cout << p->m_nRootId << " ";
	}
}

下面是main.cpp文件

#include <iostream>
#include "BinaryTreeNode.h"
using namespace std;

int main()
{
	int data[9] = { 6, 7, 2, 9, 3, 1, 8, 2, 4 };

	BinaryTree bt;
	for (int i = 0; i < 9; i++)
		bt.InsertNode(data[i]);


	cout << "*******递归算法********" << endl;
	cout << "前序遍历结果是：" << endl;
	bt.PreorderTraversal(bt.m_pTreeNode);

	cout << endl;

	cout << "中序遍历结果是：" << endl;
	bt.InorderTraversal(bt.m_pTreeNode);

	cout << endl;

	cout << "后序遍历结果是：" << endl;
	bt.PostSequenceTraversal(bt.m_pTreeNode);

	cout << endl;
	cout << endl;

	cout << "*******非递归算法********" << endl;
	cout << "前序遍历结果是：" << endl;
	bt.PreorderTraversal();

	cout << endl;
	cout << "中序遍历结果是：" << endl;
	bt.InorderTraversal();

	cout << endl;
	cout << "后序遍历结果是：" << endl;
	bt.PostSequenceTraversal();
	
	cout << endl;
	cout << "广度优先遍历结果是：" << endl;
	bt.levelOrderTraversal();

	system("pause");
	return 0;
}