神经网络模型剪枝简单理解（基于tfmot）

最近在学习模型剪枝的方法，尝试了TF官方的模型剪枝工具tfmot，这里对目前学习到的模型剪枝做简单总结。学习过程中参考了Sayak Paul的一篇文章Scooping into Model Pruning in Deep Learning

1 概念

剪枝是将神经网络中的不重要参数置为0

2 引入

考虑函数 f(x) = x + 5x²，系数分别为1和5。下图可以看到，当第一个参数发生变化时，函数的输出不会发生太大变化。故舍弃这些系数并不会真正改变函数的行为。

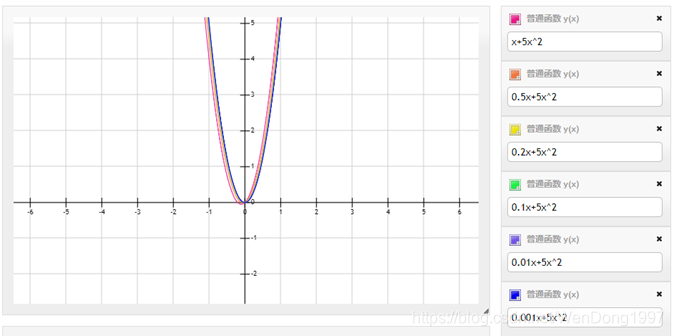
同理可以应用到神经网络，在梯度下降的优化过程中，并不是所有的权重都使用相同的梯度幅度进行更新，某些权重比其他权重的梯度幅度更大，优化器认为这些权重很重要，可以最大程度地减少训练。

3 过程

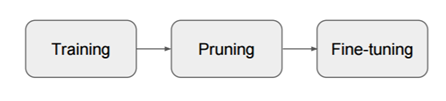
1）训练一个大的过参数化模型
2）根据某个标准修剪训练好的模型
3）微调修剪后的模型，以恢复损失的性能

4 权重筛选

可以指定一个阈值，并且所有大小超过该阈值的权重都将被认为是重要的。
1） 阈值可以是整个网络内部最低的权重值
2） 阈值可以是网络内部各层本身的权重值。在这种情况下，重要的权重会逐层过滤掉。

5 举例

在基于幅度的修剪中，将权重大小视为修剪的标准。假设输入层中有3个神经元，接受形状为（1，2）。
我们想要裁剪掉权重矩阵中70%的参数，代码实现如下：

# 复制内核权重并获取列级L2范数的排名索引
kernel_weights = np.copy(k_weights)
ind = np.argsort(np.linalg.norm(kernel_weights, axis=0))
    
# 定义索引将被置为0的数量
sparsity_percentage = 0.7
cutoff = int(len(ind)*sparsity_percentage)

# 将2D kernel权重矩阵中的索引设置为0
sparse_cutoff_inds = ind[0:cutoff]
kernel_weights[:,sparse_cutoff_inds] = 0.

权重学习后发生的变换如下图所示

但在我自己运行代码的时候发现第一步提取出的L2范数并不是图上那样，不过最终裁剪后的结果是一样的

[[-0.47114336  0.44482768  0.0658505 ]
 [ 0.4070598   0.43012297 -0.7560419 ]] 

[0.62263452 0.61877091 0.75890424]

[1 0 2] 

[[ 0.         0.         0.0658505]
 [ 0.         0.        -0.7560419]]

【注】
在修剪网络后对其进行重新训练，以补偿其性能的下降。进行此类重新训练时，必须注意修剪后的权重不会在重新训练期间进行更新。
L1正则化惩罚非零参数，导致更多的参数接近零。这在修剪之后，重新训练之前，提供了更好的准确性。然而，其余的连接不如L2正规化的好，导致再训练后精度较低。总的来说，L2正则化给出了最好的剪枝结果。

附代码中涉及到的np方法
1）np.linalg.norm()
参考 https://blog.csdn.net/hqh131360239/article/details/79061535
2）np.argsort()
作用：返回数组中从小到大的元素的索引