现代通信原理5.3: 窄带高斯白噪声
3、窄带高斯白噪声
下面我们用分析窄带高斯白噪声的复包络(低通)表示。对于窄带高斯白噪声
n
(
t
)
n(t)
n(t),我们可以求得它的解析信号以及复包络分别为
z
n
(
t
)
=
n
(
t
)
+
j
n
^
(
t
)
,
z_n(t)=n(t)+j\hat n(t),
zn(t)=n(t)+jn^(t),进一步,可以得到
x
(
t
)
x(t)
x(t)的复包络信号为
n
L
(
t
)
=
z
n
(
t
)
e
−
j
2
π
f
0
t
=
n
c
(
t
)
+
j
n
s
(
t
)
\begin{aligned} n_L(t)&=z_n(t)e^{-j2\pi f_0t}\\ &=n_c(t)+jn_s(t) \end{aligned}
nL(t)=zn(t)e−j2πf0t=nc(t)+jns(t)这里的
n
c
(
t
)
n_c(t)
nc(t)和
n
s
(
t
)
n_s(t)
ns(t)分别为
n
(
t
)
n(t)
n(t)的同相和正交分量。因此,我们可以将
n
(
t
)
n(t)
n(t)表示为
n
(
t
)
=
n
c
(
t
)
cos
2
π
f
0
t
−
n
s
(
t
)
sin
2
π
f
0
t
.
n(t)=n_c(t)\cos 2\pi f_0t-n_s(t)\sin 2\pi f_0t.
n(t)=nc(t)cos2πf0t−ns(t)sin2πf0t.这意味着,我们可以将带通噪声
n
(
t
)
n(t)
n(t)看成是两个低通噪声,
n
c
(
t
)
n_c(t)
nc(t)和
n
s
(
t
)
n_s(t)
ns(t)分别乘以同相载波
cos
2
π
f
0
t
\cos2 \pi f_0t
cos2πf0t和正交载波
−
sin
2
π
f
0
t
-\sin 2\pi f_0t
−sin2πf0t。需要注意的是,此时带通噪声
n
(
t
)
n(t)
n(t)、复包络同相分量
n
c
(
t
)
n_c(t)
nc(t)和正交分量$n_s(t)的均值和方差满足
E
[
n
(
t
)
]
=
E
[
n
c
(
t
)
]
=
E
[
n
s
(
t
)
]
=
0
,
E
[
n
2
(
t
)
]
=
E
[
n
c
2
(
t
)
]
=
E
[
n
s
2
(
t
)
]
=
σ
n
2
.
\begin{aligned} &{\rm E}[n(t)]={\rm E}[n_c(t)]={\rm E}[n_s(t)]=0,\\ &{\rm E}[n^2(t)]={\rm E}[n^2_c(t)]={\rm E}[n^2_s(t)]=\sigma_n^2. \end{aligned}
E[n(t)]=E[nc(t)]=E[ns(t)]=0,E[n2(t)]=E[nc2(t)]=E[ns2(t)]=σn2.即它们均值都为零,功率相等,我们用
σ
n
2
\sigma_n^2
σn2表示。
我们以白噪声通过DSB-SC解调器为例来分析这个问题,如图1所示。
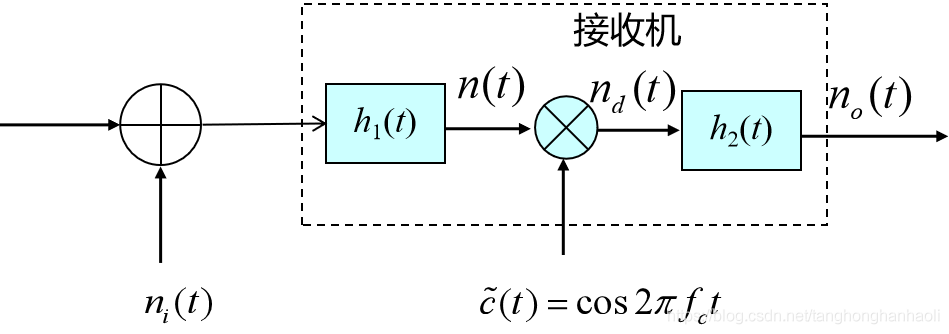
在图1中,
n
i
(
t
)
n_i(t)
ni(t)为理想白噪声,其功率谱密度为
P
N
i
(
f
)
=
n
0
2
,
−
∞
<
f
<
∞
,
P_{N_i}(f)=\frac{n_0}{2},\ -\infty <f<\infty,
PNi(f)=2n0, −∞<f<∞,经过带通滤波器
H
1
(
f
)
H_1(f)
H1(f)之后的输出
n
(
t
)
n(t)
n(t)的功率谱密度为
P
N
(
f
)
=
P
N
i
(
f
)
∣
H
1
(
f
)
∣
2
,
P_N(f)=P_{N_i}(f)|H_1(f)|^2,
PN(f)=PNi(f)∣H1(f)∣2,这里的
∣
H
1
(
f
)
∣
2
|H_1(f)|^2
∣H1(f)∣2为滤波器|H_1(f)|的功率传递函数。由于
H
1
(
f
)
=
R
e
c
t
(
f
−
f
0
B
)
+
R
e
c
t
(
f
+
f
0
B
)
H_1(f)={\rm Rect}{\Large (}\frac{f-f_0}{B}{\Large )}+{\rm Rect}{\Large (}\frac{f+f_0}{B}{\Large )}
H1(f)=Rect(Bf−f0)+Rect(Bf+f0),因此可以得到
P
N
(
f
)
=
{
n
0
2
,
f
0
−
B
2
<
∣
f
∣
<
f
0
+
B
2
0
,
其
它
P_{N}(f)=\left\{ \begin{aligned} \frac{n_0}{2},\ &f_0-\frac{B}{2} <|f|<f_0+\frac{B}{2}\\ 0,\ &\rm 其它 \end{aligned}\right.
PN(f)=⎩⎨⎧2n0, 0, f0−2B<∣f∣<f0+2B其它或者表示为
P
N
(
f
)
=
n
0
2
[
R
e
c
t
(
f
−
f
0
B
)
+
R
e
c
t
(
f
+
f
0
B
)
]
.
P_N(f)=\frac{n_0}{2}{\Large [}{\rm Rect}{\Large (}\frac{f-f_0}{B}{\Large )}+{\rm Rect}{\Large (}\frac{f+f_0}{B}{\Large )}{\Large ]}.
PN(f)=2n0[Rect(Bf−f0)+Rect(Bf+f0)].
P
N
i
(
f
)
P_{N_i}(f)
PNi(f)与
P
N
(
f
)
P_N(f)
PN(f)的示意图分别如图2(a)(b)所示。
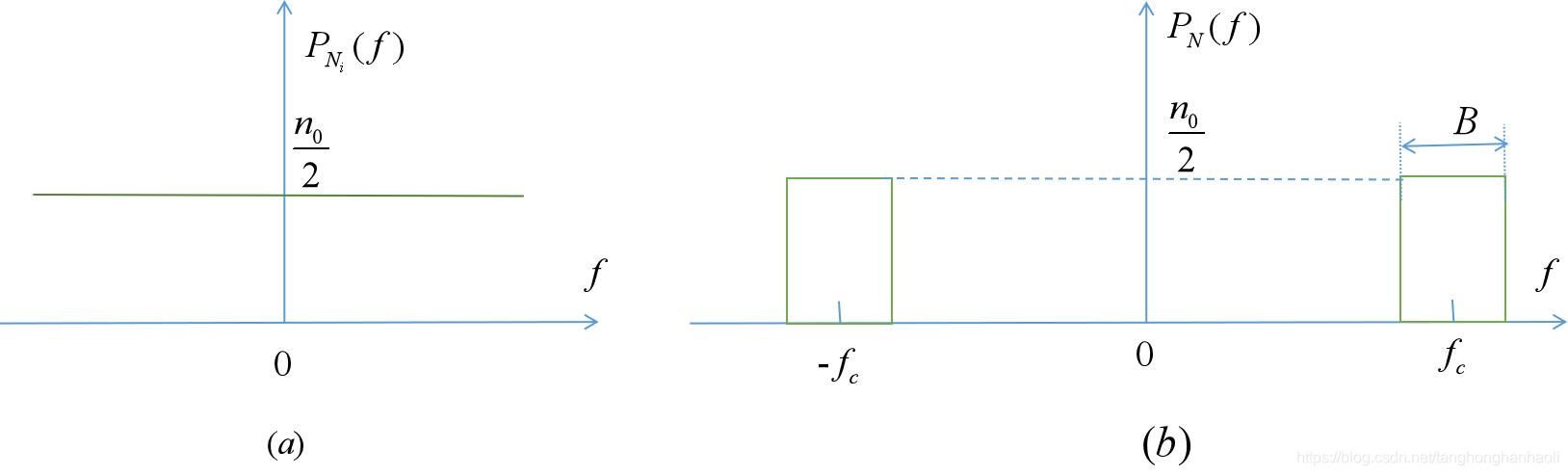
下面我们来分析带通随机过程
n
(
t
)
n(t)
n(t)的复包络。显然有
n
(
t
)
=
n
c
(
t
)
cos
2
π
f
c
t
−
n
s
(
t
)
sin
2
π
f
c
t
.
n(t)=n_c(t)\cos 2\pi f_ct-n_s(t)\sin 2\pi f_ct.
n(t)=nc(t)cos2πfct−ns(t)sin2πfct.进一步,如图(1)所示,带通白噪声
n
(
t
)
n(t)
n(t)与频率为
f
c
f_c
fc的载波信号相乘,即
n
d
(
t
)
=
n
(
t
)
cos
2
π
f
c
t
=
n
c
(
t
)
cos
2
2
π
f
c
t
−
n
s
(
t
)
sin
2
π
f
c
t
cos
2
π
f
c
t
=
1
2
n
c
(
t
)
+
1
2
n
c
(
t
)
cos
4
π
f
c
t
−
1
2
n
s
(
t
)
sin
4
π
f
c
t
\begin{aligned} n_d(t)&=n(t)\cos 2\pi f_ct\\ &=n_c(t)\cos^2 2\pi f_ct-n_s(t)\sin 2\pi f_ct \cos 2\pi f_ct\\ &=\frac{1}{2}n_c(t)+\frac{1}{2}n_c(t)\cos 4\pi f_ct-\frac{1}{2}n_s(t)\sin 4\pi f_ct \\ \end{aligned}
nd(t)=n(t)cos2πfct=nc(t)cos22πfct−ns(t)sin2πfctcos2πfct=21nc(t)+21nc(t)cos4πfct−21ns(t)sin4πfct显然,经过低通滤波器
H
2
(
f
)
H_2(f)
H2(f),可以将两倍载频处的噪声滤掉,得到
n
o
(
t
)
=
1
2
n
c
(
t
)
,
n_o(t)=\frac{1}{2}n_c(t),
no(t)=21nc(t),其平均功率为
P
N
o
(
f
)
=
1
4
E
[
n
c
2
(
t
)
]
=
σ
n
2
4
=
1
4
P
N
(
f
)
,
\begin{aligned} P_{N_o}(f)=\frac{1}{4}{\rm E}[n_c^2(t)]=\frac{\sigma_n^2}{4}=\frac{1}{4}P_N(f), \end{aligned}
PNo(f)=41E[nc2(t)]=4σn2=41PN(f),这里
P
N
(
f
)
P_N(f)
PN(f)的带通白噪声
n
(
t
)
n(t)
n(t)的平均功率。在《MATLAB通信仿真实例2:白噪声通过DSB-SC解调器》中,我们用功率谱密度分析了带通噪声通过DSB-SC解调器各点的功率谱密度,大家可以与这里讨论的带通噪声低通表示对照来看,会发现最终对输出功率的分析是一致的。