算法比赛复习
陆陆续续四个多月的学习小总结,具体题目和题解在下方:
写了这个总结后,又做了一些真题,结果发现是一些特性不符合比赛的编译器版本,所以有些基础的转换还不太行,还有一些奇怪的输入,其他的都还好,我寻思着,这比赛不考多点算法的东西,整这么多奇葩的输入干啥。
字串问题 和 并查集 和 大数问题(以及进制) 需要补充
容器以及algorithm算法部分
对以下容器和不同类型数组的使用有一定的理解
string,
vector,list,deque,
queue,stack,
priority_queue
set,unorder_set,
map,unorder_map
father数组,树状数组
a[] a[][] a[][][]algorithm库的使用 max,min
*max_element,*min_element
sort,heap_sort
next_permutation
fill memset
swap
reverse
lower_bound,upper_bound
算法部分
1.递归{ ①1.92. 递归实现指数型枚举 ②. 93. 递归实现组合型枚举 ③. 94. 递归实现排列型枚举 }
。
2.dfs{ ①迷宫问题 ②固定方向路径数问题 ③皇后问题 (dfs+回溯) }
。
3.bfs与逆向bfs{ ①迷宫问题 ②单源到单源单位长读最短路径 }
。
4.回溯(dfs+回溯){ ①全排列问题 ②括号生成与括号配对问题 ③皇后问题 ④岛屿问题 }
。
5.最小生成树(kruscal+并查集){ ①抽象成点的连接的最小代价问题 ②村庄(城市)通路问题 }
。
6.单源到多源最短路(dijkstra){ 从某个点i到其他任一点的最短距离 }
。
7.多源到多源(floyd){ 抽象成n个点两两最短路问题 }
。
8.拓扑排序{ 做一系列的事情,需要前置条件 ①课程表 }
。
9.dp{ 1)线性dp: ①路径问题 ②背包九讲 ③不相邻背包 ④序列和以及序列最值问题 ⑤记忆化搜索dsf+dp 2)区间dp: ①区间dp转换成线性dp 最长公共子序列 }
。
10.各种排序{ 插入排序,二分插入排序,希尔排序,选择排序,堆排序,冒泡排序,归并排序,快排 }
。
11.数学问题(GCD,快速幂,矩阵快速幂){ ①GCD ②快速幂 ③矩阵快速幂 ④朴素素数 ⑤埃筛 ⑥欧拉筛 }
。
12.前缀和{ ①一维前缀和 ②子矩阵和 ③树状数组解决 前缀和 以及 动态数组的插入问题 }
。
13.二分思想{ 找一个开区间,使得ans一定在区间里, 对半分区间,并且具有二段性(有且仅有一个区间存在ans) ans一定在左区间的右端点,或右区间的左端点。 因此每次更新l或r,都设置为区间的端点。 最终若端点为ans即存在,否则不存在。
①模板1: 确认ans在左区间-> r=m; m的计算保持不变。 ②模板2: 确认ans在右区间->l=m;
m的计算应该改为:m=(l+r+1)/2; }。===========================================================
。
最后需要学习的东西:
1.set map 操作 √
2.二分,前缀和 √
3.一道递归题 1h33’ -2h6’
4.一道模拟排序:1h9’ -1h25’
5.树状数组、线段树 √ ⚪
6.贪心
题外话:解除cin和stdio同步,cin和cout速度与scanf printf同样
ios::sync_with_stdio(false);
dfs+回溯 (dfs暴力 dfs剪枝)
1.岛屿的个数
2.岛屿的最大面积
3.全排列
5.解迷宫
6.踩方格
8.括号生成
9.单源到单源最短路径
(这个和迷宫一个道理,返回最短的路径就可以了,还有一个剪枝的技巧,一旦tem_len>min_len 直接return
大白话就是,如果在路径长度累加的过程中,一旦出现当前累加长度大于原来存储的最短长度,那么不需要继续走下去了,直接返回 )
10.盾神与砝码称重
BFS
1.迷宫求解
2.最短路径(格子的长度为1,无权值 的)
3.01矩阵
4.地牢大师
5.全球变暖
最小生成树--------kruscal克鲁斯卡尔(并查集)
1.村庄通电【模板】
2.并查集-模板题+练习题
单源最短路dijkstra
1.dijkstra
拓扑排序
1.课程表
2.课程表Ⅱ(课程表的衍生物)
Excel
日期快速获取:
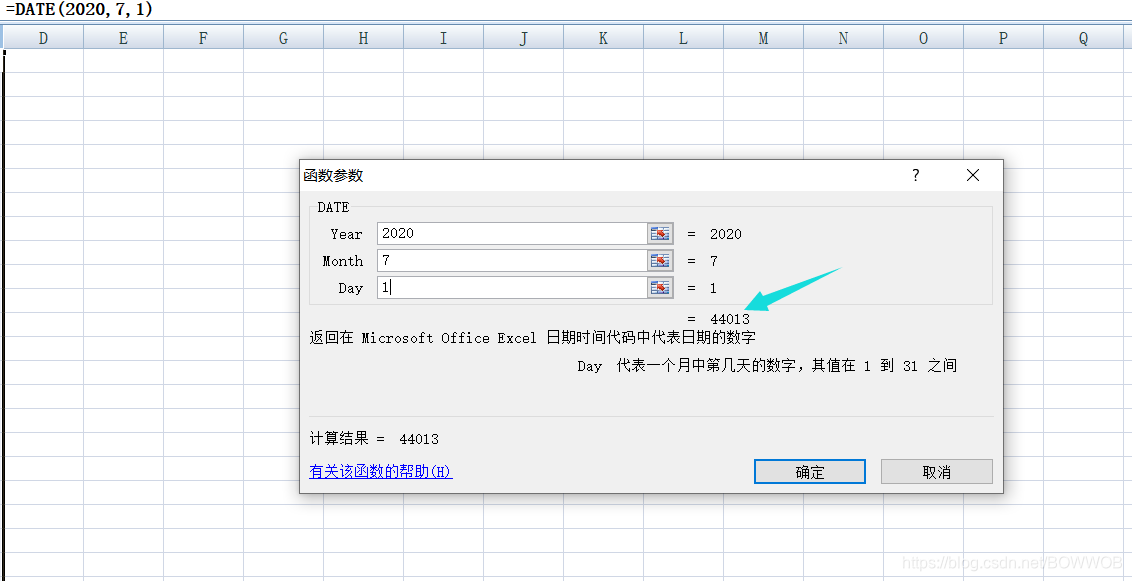
动态规划DP
经典DP问题(leetcode简单题 自定义排序)
1)路径 背包 问题dp
2)序列 线性dp问题
3)区间dp
一.背包九讲
二.搜索dfs+备忘录(记忆化搜索)
1.滑雪经典题
贪心 类型题
递归
1.92. 递归实现指数型枚举
2. 93. 递归实现组合型枚举
3. 94. 递归实现排列型枚举
各种排序
二分思想
模拟
数学问题
前缀和
容器使用
0.set和map和unordered_set 和unorded_map 的基本操作
4.all_sort
ASCII
任意类型的转换
容器的增删改查以及顺序
初始状态
字符串和字符数组
string整体大小写转换函数
熟悉的算法: 枚举 暴力for dfs bfs 回溯 并查集 最小生成树 拓扑排序
数学算法: 快速幂 gcd lcm
输入的正确性的确保
测试用例的种类
时间复杂度的分析