凸优化学习笔记17:次梯度下降法
对于光滑函数,我们可以用梯度下降法,并且证明了取不同的步长,可以得到次线性收敛,如果加上强凸性质,还可以得到线性收敛速度。那如果现在对于不可导的函数,我们就只能沿着次梯度下降,同样会面临步长的选择、方向的选择、收敛性分析等问题。
1. 收敛性分析
次梯度下降的一般形式为
x
(
k
)
=
x
(
k
−
1
)
−
t
k
g
(
k
−
1
)
,
k
=
1
,
2
,
…
g
∈
∂
f
(
x
(
k
−
1
)
)
x^{(k)}=x^{(k-1)}-t_{k} g^{(k-1)}, \quad k=1,2, \ldots \quad g\in\partial f(x^{(k-1)})
x(k)=x(k−1)−tkg(k−1),k=1,2,…g∈∂f(x(k−1))
一般有 3 种步长的选择方式:
- fix step: t k t_k tk 为常数
- fix length: t k ∥ g ( k − 1 ) ∥ 2 = ∥ x ( k ) − x ( k − 1 ) ∥ 2 t_{k}\left\|g^{(k-1)}\right\|_{2}=\left\|x^{(k)}-x^{(k-1)}\right\|_{2} tk∥∥g(k−1)∥∥2=∥∥x(k)−x(k−1)∥∥2 为常数
- diminishing: t k → 0 , ∑ k = 1 ∞ t k = ∞ t_{k} \rightarrow 0, \sum_{k=1}^{\infty} t_{k}=\infty tk→0,∑k=1∞tk=∞
要证明这几种方法的收敛性,需要先引入 Lipschitz continuous 假设,即
∣
f
(
x
)
−
f
(
y
)
∣
≤
G
∥
x
−
y
∥
2
∀
x
,
y
|f(x)-f(y)| \leq G\|x-y\|_{2} \quad \forall x, y
∣f(x)−f(y)∣≤G∥x−y∥2∀x,y
这等价于
∥
g
∥
2
≤
G
\Vert g\Vert_2\le G
∥g∥2≤G 对任意
g
∈
∂
f
(
x
)
g\in\partial f(x)
g∈∂f(x) 都成立。
在分析收敛性之前,我们需要引入一个非常重要的式子⬇️!!!在后面的分析中会一直用到:
∥
x
+
−
x
⋆
∥
2
2
=
∥
x
−
t
g
−
x
⋆
∥
2
2
=
∥
x
−
x
⋆
∥
2
2
−
2
t
g
T
(
x
−
x
⋆
)
+
t
2
∥
g
∥
2
2
≤
∥
x
−
x
⋆
∥
2
2
−
2
t
(
f
(
x
)
−
f
⋆
)
+
t
2
∥
g
∥
2
2
\begin{aligned} \left\|x^{+}-x^{\star}\right\|_{2}^{2} &=\left\|x-t g-x^{\star}\right\|_{2}^{2} \\ &=\left\|x-x^{\star}\right\|_{2}^{2}-2 t g^{T}\left(x-x^{\star}\right)+t^{2}\|g\|_{2}^{2} \\ & \leq\left\|x-x^{\star}\right\|_{2}^{2}-2 t\left(f(x)-f^{\star}\right)+t^{2}\|g\|_{2}^{2} \end{aligned}
∥∥x+−x⋆∥∥22=∥x−tg−x⋆∥22=∥x−x⋆∥22−2tgT(x−x⋆)+t2∥g∥22≤∥x−x⋆∥22−2t(f(x)−f⋆)+t2∥g∥22
那么如果定义
f
b
e
s
t
(
k
)
=
min
0
≤
i
<
k
f
(
x
(
i
)
)
f_{\mathrm{best}}^{(k)}=\min _{0 \leq i<k} f\left(x^{(i)}\right)
fbest(k)=min0≤i<kf(x(i)),就有
2
(
∑
i
=
1
k
t
i
)
(
f
best
(
k
)
−
f
⋆
)
≤
∥
x
(
0
)
−
x
⋆
∥
2
2
−
∥
x
(
k
)
−
x
⋆
∥
2
2
+
∑
i
=
1
k
t
i
2
∥
g
(
i
−
1
)
∥
2
2
≤
∥
x
(
0
)
−
x
⋆
∥
2
2
+
∑
i
=
1
k
t
i
2
∥
g
(
i
−
1
)
∥
2
2
\begin{aligned} 2\left(\sum_{i=1}^{k} t_{i}\right)\left(f_{\text {best }}^{(k)}-f^{\star}\right) & \leq\left\|x^{(0)}-x^{\star}\right\|_{2}^{2}-\left\|x^{(k)}-x^{\star}\right\|_{2}^{2}+\sum_{i=1}^{k} t_{i}^{2}\left\|g^{(i-1)}\right\|_{2}^{2} \\ & \leq\left\|x^{(0)}-x^{\star}\right\|_{2}^{2}+\sum_{i=1}^{k} t_{i}^{2}\left\|g^{(i-1)}\right\|_{2}^{2} \end{aligned}
2(i=1∑kti)(fbest (k)−f⋆)≤∥∥∥x(0)−x⋆∥∥∥22−∥∥∥x(k)−x⋆∥∥∥22+i=1∑kti2∥∥∥g(i−1)∥∥∥22≤∥∥∥x(0)−x⋆∥∥∥22+i=1∑kti2∥∥∥g(i−1)∥∥∥22
根据上面的式子,就可以得到对于
Fixed step size:
t
i
=
t
t_i=t
ti=t
f
best
(
k
)
−
f
⋆
≤
∥
x
(
0
)
−
x
⋆
∥
2
2
2
k
t
+
G
2
t
2
f_{\text {best }}^{(k)}-f^{\star} \leq \frac{\left\|x^{(0)}-x^{\star}\right\|_{2}^{2}}{2 k t}+\frac{G^{2} t}{2}
fbest (k)−f⋆≤2kt∥∥x(0)−x⋆∥∥22+2G2t
Fixed step length:
t
i
=
s
/
∥
g
(
i
−
1
)
∥
2
t_{i}=s /\left\|g^{(i-1)}\right\|_{2}
ti=s/∥∥g(i−1)∥∥2
f
best
(
k
)
−
f
⋆
≤
G
∥
x
(
0
)
−
x
⋆
∥
2
2
2
k
s
+
G
s
2
f_{\text {best }}^{(k)}-f^{\star} \leq \frac{G\left\|x^{(0)}-x^{\star}\right\|_{2}^{2}}{2 k s}+\frac{G s}{2}
fbest (k)−f⋆≤2ksG∥∥x(0)−x⋆∥∥22+2Gs
这两个式子中的第一项都随着
k
k
k 增大而趋于 0,但第二项却没有办法消掉,也就是与最优解的误差不会趋于 0。并且他们有一个微妙的不同点在于,fixed step size 情况下
G
2
t
/
2
∼
O
(
G
2
)
,
G
s
/
2
∼
O
(
G
)
G^2t/2\sim O(G^2),Gs/2\sim O(G)
G2t/2∼O(G2),Gs/2∼O(G),
G
G
G 一般是较大的。
Diminishing step size:
t
k
→
0
,
∑
k
=
1
∞
t
k
=
∞
t_{k} \rightarrow 0, \sum_{k=1}^{\infty} t_{k}=\infty
tk→0,∑k=1∞tk=∞
f
best
(
k
)
−
f
⋆
≤
∥
x
(
0
)
−
x
⋆
∥
2
2
+
G
2
∑
i
=
1
k
t
i
2
2
∑
i
=
1
k
t
i
f_{\text {best }}^{(k)}-f^{\star} \leq \frac{\left\|x^{(0)}-x^{\star}\right\|_{2}^{2}+G^{2} \sum_{i=1}^{k} t_{i}^{2}}{2 \sum_{i=1}^{k} t_{i}}
fbest (k)−f⋆≤2∑i=1kti∥∥x(0)−x⋆∥∥22+G2∑i=1kti2
可以证明,
(
∑
i
=
1
k
t
i
2
)
/
(
∑
i
=
1
k
t
i
)
→
0
\left(\sum_{i=1}^{k} t_{i}^{2}\right) /\left(\sum_{i=1}^{k} t_{i}\right) \rightarrow 0
(∑i=1kti2)/(∑i=1kti)→0,因此
f
best
(
k
)
f_{\text {best }}^{(k)}
fbest (k) 会收敛于
f
⋆
f^\star
f⋆。
下面看几幅图片,对于优化问题 min ∥ A x − b ∥ 1 \min\Vert Ax-b\Vert_1 min∥Ax−b∥1
| Fixed step length | Diminishing step size |
|---|---|
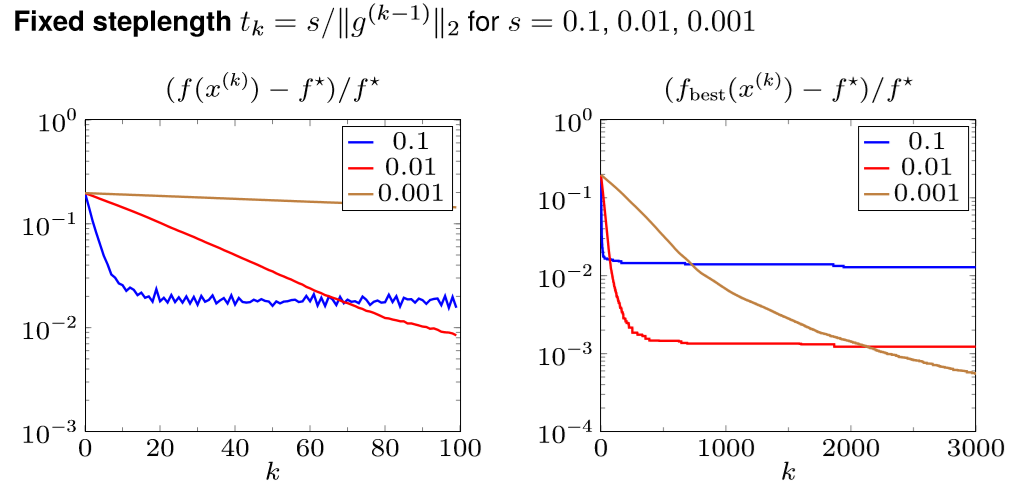 | 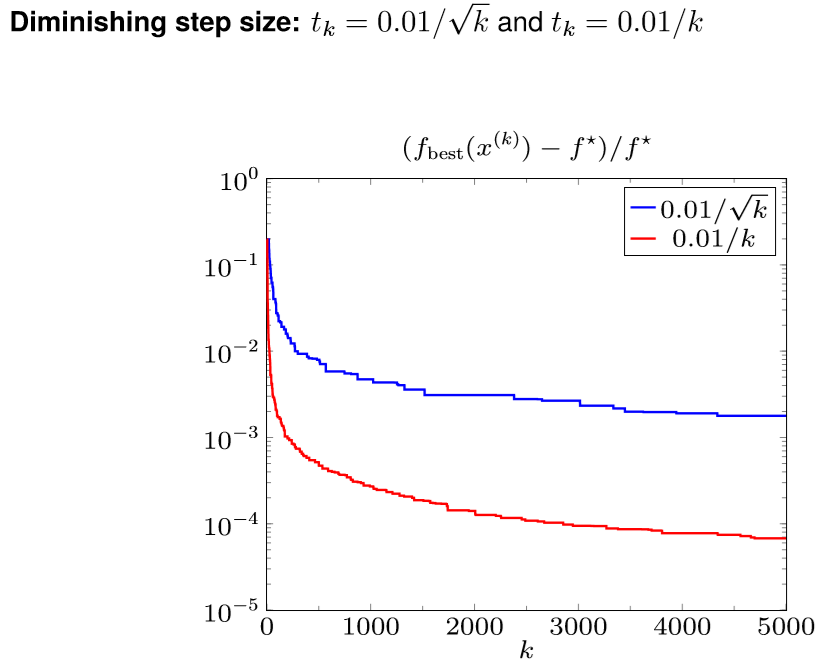 |
前面考虑了固定步长的情况,假设现在我们固定总的迭代次数为
k
k
k,可不可以优化步长
s
s
s 的大小来尽可能使
f
best
(
k
)
f_\text{best}^{(k)}
fbest(k) 接近
f
⋆
f^\star
f⋆ 呢?这实际上可以表示为优化问题
f
best
(
k
)
−
f
⋆
≤
R
2
+
∑
i
=
1
k
s
i
2
2
∑
i
=
1
k
s
i
/
G
⟹
min
s
R
2
2
k
s
/
G
+
s
2
/
G
f_{\text {best }}^{(k)}-f^{\star} \leq \frac{R^{2}+\sum_{i=1}^{k} s_{i}^{2}}{2 \sum_{i=1}^{k} s_{i}/G} \Longrightarrow \min_s \frac{R^{2}}{2 ks/G}+\frac{s}{2/G}
fbest (k)−f⋆≤2∑i=1ksi/GR2+∑i=1ksi2⟹smin2ks/GR2+2/Gs
其中
R
=
∥
x
(
0
)
−
x
⋆
∥
2
R=\left\|x^{(0)}-x^{\star}\right\|_{2}
R=∥∥x(0)−x⋆∥∥2,那么最优步长为
s
=
R
/
k
s=R/\sqrt{k}
s=R/k,此时
f
best
(
k
)
−
f
⋆
≤
G
R
k
f_{\text {best }}^{(k)}-f^{\star} \leq \frac{GR}{\sqrt{k}}
fbest (k)−f⋆≤kGR
因此收敛速度为
O
(
1
/
k
)
O(1/\sqrt{k})
O(1/k),对比之前光滑函数的梯度下降,收敛速度为
O
(
1
/
k
)
O(1/k)
O(1/k)。
我们对前面的收敛速度并不满意,如果有更多的信息,比如已知最优解
f
⋆
f^\star
f⋆ 的大小,能不能改进收敛速度呢?根据前面的式子,有
∥
x
+
−
x
⋆
∥
2
2
≤
∥
x
−
x
⋆
∥
2
2
−
2
t
i
(
f
(
x
)
−
f
⋆
)
+
t
i
2
∥
g
∥
2
2
\left\|x^{+}-x^{\star}\right\|_{2}^{2} \leq\left\|x-x^{\star}\right\|_{2}^{2}-2 t_i\left(f(x)-f^{\star}\right)+t_i^{2}\|g\|_{2}^{2}
∥∥x+−x⋆∥∥22≤∥x−x⋆∥22−2ti(f(x)−f⋆)+ti2∥g∥22
这实际上是关于
t
i
t_i
ti 的一个二次函数,因此可以取
t
i
=
f
(
x
(
i
−
1
)
)
−
f
⋆
∥
g
(
i
−
1
)
∥
2
2
t_{i}=\frac{f\left(x^{(i-1)}\right)-f^{\star}}{\left\|g^{(i-1)}\right\|_{2}^{2}}
ti=∥g(i−1)∥22f(x(i−1))−f⋆,就可以得到
f
best
(
k
)
−
f
⋆
≤
G
R
k
f_{\text {best }}^{(k)}-f^{\star} \leq \frac{GR}{\sqrt{k}}
fbest (k)−f⋆≤kGR
可见还是没有改进收敛速度。
如果引入强凸性质呢?如果假设满足
μ
\mu
μ 强凸,则
f
⋆
≥
f
k
+
g
k
T
(
x
k
−
x
⋆
)
+
μ
/
2
∥
x
k
−
x
⋆
∥
2
2
f^\star \ge f^k+g^{kT}(x^k-x^\star)+\mu/2\Vert x^k-x^\star\Vert_2^2
f⋆≥fk+gkT(xk−x⋆)+μ/2∥xk−x⋆∥22,可以取
t
k
=
2
μ
(
k
+
1
)
t_k=\frac{2}{\mu(k+1)}
tk=μ(k+1)2,那么就可以得到
f
best
(
k
)
−
f
⋆
≤
2
G
2
μ
(
k
+
1
)
f_{\text {best }}^{(k)}-f^{\star} \leq \frac{2G^2}{\mu(k+1)}
fbest (k)−f⋆≤μ(k+1)2G2
最后给我的博客打个广告,欢迎光临
https://glooow1024.github.io/
https://glooow.gitee.io/
前面的一些博客链接如下
凸优化专栏
凸优化学习笔记 1:Convex Sets
凸优化学习笔记 2:超平面分离定理
凸优化学习笔记 3:广义不等式
凸优化学习笔记 4:Convex Function
凸优化学习笔记 5:保凸变换
凸优化学习笔记 6:共轭函数
凸优化学习笔记 7:拟凸函数 Quasiconvex Function
凸优化学习笔记 8:对数凸函数
凸优化学习笔记 9:广义凸函数
凸优化学习笔记 10:凸优化问题
凸优化学习笔记 11:对偶原理
凸优化学习笔记 12:KKT条件
凸优化学习笔记 13:KKT条件 & 互补性条件 & 强对偶性
凸优化学习笔记 14:SDP Representablity
凸优化学习笔记 15:梯度方法
凸优化学习笔记 16:次梯度
凸优化学习笔记 17:次梯度下降法