水排序谜题
目录
一,背景
本游戏是我在总结出启发式游戏综述启发式游戏综述_nameofcsdn的博客-CSDN博客之后的第一个实践,我将用模型的语言来表达。
按照这个模型,本游戏和华容道汽车华容道_nameofcsdn的博客-CSDN博客_汽车华容道160关攻略其实很像。
二,水排序谜题

通过把水倒来倒去,最终同色水都在一个试管内即可。
任何水都可以倒入空试管,如果是非空试管,那么只有同色水可以倒入,
试管满了就不能再倒了,实际上试管的大小就是4,单份水的大小就是1
为了方便描述,这里统一术语
元素:一个试管内,1份或多份同色相连的水,叫一个元素
试管对称性:最终状态下,各色水和各试管并没有固定的对应关系,实际上,水和试管的任何对应关系都是可达状态。
三,状态空间
所有试管内的水构成一个状态,一次倒水就是一次状态转移,这种状态转移是不可逆的。
状态空间是有向图,在试管对称性的意义上,有唯一目标状态。
状态空间很接近树,因为没有有向环,无向环也很少。
所以,这个游戏大部分时候面临的选择都很少,
四,全局状态策略
如果1个试管是上A下B,另外1个试管是上B下A,那么至少要另外一个辅助试管,才能完成水排序。(参见下文死锁模型)
如果情况复杂一点,多个试管内的元素都是交叉覆盖的,就会出现至少需要两个辅助试管的情况。
总之,我们首先得到一个全局策略:
每隔一段操作,就会出现一次状态转移,从没有空试管,变成有一个空试管。
如第13关:



到这里,后面就没什么难度了。
五,局部启发式策略——关键颜色策略
1,辅助信息——关键颜色
这个游戏需要的辅助信息属于比较明显的类型,那就是对于初始状态,我们应该把哪个颜色的元素倒入空试管呢?
我把这个叫做关键颜色。
2,辅助信息如何指导我们找到解
策略指导我们,把关键颜色的元素倒入空试管之后,尽可能多的把同色元素都倒入此试管,这样其他试管才有足够空间来调度。
3,如何确定关键颜色
我以实际关卡为例,从简至深地阐述如何确定关键颜色
(1)距离管口的位置
第13关:
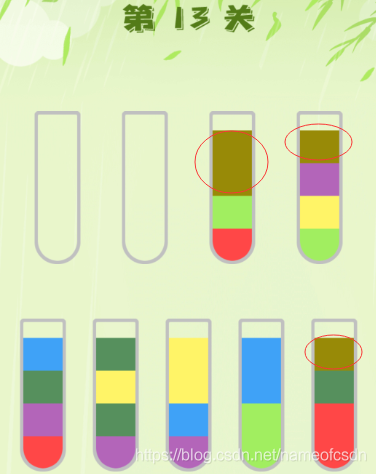
棕色元素都在各试管上面,所以它就是关键颜色
(2)被压制的颜色数
第14关:
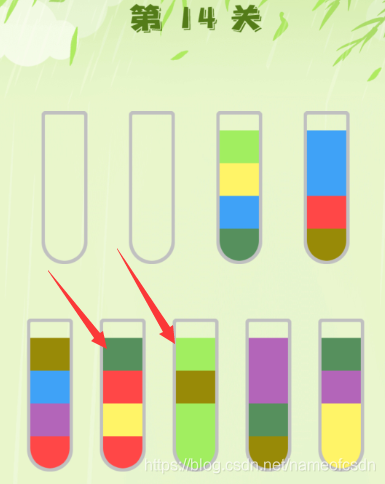
青色只被一个颜色压制,而绿色被4个颜色压制,所以关键色是青色

(3)关键颜色的本质
关键颜色的本质,其实就是利用位置关系,推算出最容易操作的颜色。
按照寻找关键色的标准,实际上我们是可以把所有颜色按照最容易操作到最难操作依次排出来的。
我们把这个属性叫做自由度,即关键颜色就是自由度最高的颜色。
(4)自由度的传递
如果一个元素被自由度很低的元素压制,那么它的自由度也会很低。
如果一个元素只被自由度很高的元素压制,那么它的自由度就不太低。
六,局部启发式策略——关键颜色进阶
1,二级关键颜色
有些局面,关键颜色很明显,而第二个颜色反而需要仔细分析,我愿称之为二级关键颜色。
第43关:

关键颜色显然是黄色,而二级关键颜色并不好找,这是本关的难点。
在合并关键色的同时,要留住一个空试管,并尽量把其他颜色能合并的就合并,

到了这一步,没法操作了,再决定哪个是二级关键颜色。
这一关的二级关键颜色是橙色或者蓝色。
同样的,第52关:

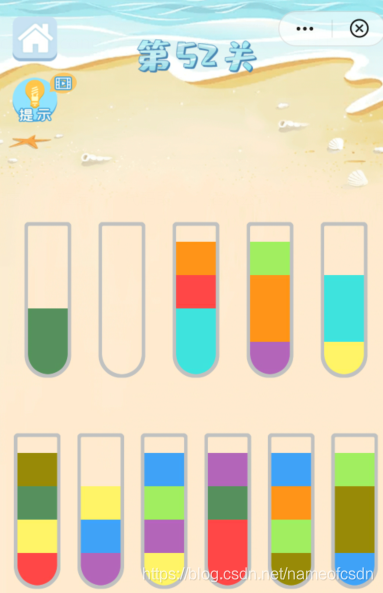
这一关的二级关键色是青色或者蓝色。
2,PageRank
自由度和PageRank算法中网页质量是类似的,自由度的传递和PageRank算法的核心思想也是一样的,
所以,理论上,PageRank算法是可以用来辅助计算关键颜色的。
代码V1.0:
#include<iostream>
#include<string>
#include<vector>
#include <algorithm>
using namespace std;
#define NC 9
vector<string>vc = { "黄色","绿色","翠绿","青色","蓝色","紫色","棕色","橙色","红色" };
vector<vector<int>>vm; //试管
vector<double>score(NC); //各色被压制程度
void OutMap()
{
for (int i=0;i<vc.size();i++)
{
cout << i << " "<<vc[i]<<" ";
}
}
void Input()
{
int a;
cout << "\n输入负载试管数目";
cin >> a;
vm.resize(a);
cout << "输入试管容量 ";
cin >> a;
for (auto &vi : vm) {
vi.resize(a);
}
cout << "依次输入各试管内颜色,从上往下\n";
for (auto &vi:vm) {
for (int j = a - 1; j >= 0; j--)cin >> vi[j];
}
}
void Init()
{
OutMap();
Input();
}
void InitScore()
{
for (double & si : score)si = 0;
for (auto vi : vm) {
for (int j = 0; j < vi.size(); j++) {
score[vi[j]] += vi.size() - j;
}
}
}
void PageRank()
{
vector<double>newScore(NC);
for (auto vi : vm) {
double s = 0;
for (int j = vi.size() - 1; j >= 0; j--) {
newScore[vi[j]] += s, s += score[vi[j]];
}
}
score = newScore;
}
template<typename T>
vector<int> sortId(vector<T>v);
void GetScore()
{
vector<int>id = sortId(score);
for (auto i : id) {
cout << vc[i] << " ";
}
cout << endl;
}
int main()
{
Init();
InitScore();
GetScore();
for (int i = 0; i < 5; i++) {
PageRank();
GetScore();
}
return 0;
}其中sortId函数来自我的模板
应用实例:
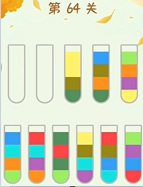
0黄色 1绿色 2翠绿 3青色 4蓝色 5紫色 6棕色 7橙色 8红色
输入:
9
4
0 0 6 1
4 6 7 1
2 7 5 0
4 3 7 2
8 3 5 7
1 8 1 2
0 6 3 5
8 6 4 3
2 5 4 8
输出:
黄色 蓝色 红色 棕色 翠绿 青色 绿色 紫色 橙色
蓝色 棕色 黄色 红色 青色 翠绿 绿色 橙色 紫色
棕色 蓝色 红色 黄色 青色 翠绿 绿色 橙色 紫色
棕色 蓝色 红色 黄色 青色 翠绿 绿色 橙色 紫色
蓝色 棕色 红色 黄色 青色 翠绿 绿色 橙色 紫色
棕色 蓝色 红色 黄色 青色 翠绿 绿色 橙色 紫色
基本上前四名是比较确定的,那么两个关键颜色就是从这四个里面出,还可以结合其他经验进一步推导。
这一关来说,选取棕色和黄色是可以的,选取蓝色和黄色也是可以的。
总体来说,这个算法有3个核心缺陷:
(1)因为有多解的情况,所以单纯的把所有颜色的自由度排序并不能很好的指导关键色的选取,最后还需要枚举或者结合其他经验。
(2)这个游戏的自由度传递,涉及的跨试管的传递模型很多,仅已单试管内的压制关系计算数值最后叠加起来,不够准确。
(3)跨试管的传递模型并不都是从上往下传递的,也有一些是从下往上传递的,比如ABCA模型。
再来看看对于69关:
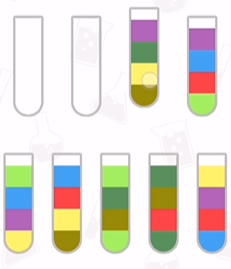
运行程序,输入:
7 4
5 1 0 6
5 4 8 2
2 4 5 0
4 8 0 6
2 1 6 2
1 6 8 1
0 5 8 4
输出:
青色 橙色 紫色 绿色 蓝色 翠绿 黄色 红色 棕色
青色 橙色 紫色 蓝色 绿色 翠绿 黄色 红色 棕色
青色 橙色 紫色 蓝色 绿色 黄色 翠绿 红色 棕色
青色 橙色 紫色 蓝色 绿色 黄色 翠绿 红色 棕色
青色 橙色 紫色 蓝色 绿色 黄色 翠绿 红色 棕色
青色 橙色 紫色 蓝色 绿色 黄色 翠绿 红色 棕色
其中,青色和橙色其实是这一关里面不存在的。
所以我做了小小的改动,同时新增了输入校验,如果输入的任何一个颜色的数目和试管容量不同,那么输入作废。
代码V1.1:
#include<iostream>
#include<string>
#include<vector>
#include <algorithm>
using namespace std;
#define NC 9
vector<string>vc = { "黄色","绿色","翠绿","青色","蓝色","紫色","棕色","橙色","红色" };
vector<vector<int>>vm; //试管
vector<double>score(NC); //各色被压制程度
int avail[NC]; //各色出现次数
void OutMap()
{
for (int i=0;i<vc.size();i++)
{
cout << i << " "<<vc[i]<<" ";
}
}
void Input()
{
int a;
cout << "\n输入负载试管数目";
cin >> a;
vm.resize(a);
cout << "输入试管容量 ";
cin >> a;
for (auto &vi : vm) {
vi.resize(a);
}
cout << "依次输入各试管内颜色,从上往下\n";
for (auto &vi:vm) {
for (int j = a - 1; j >= 0; j--)cin >> vi[j], avail[vi[j]]++;
}
}
bool Check()
{
int a = vm[0].size();
for (int i = 0; i < NC; i++)if (avail[i] != 0 && avail[i] != a)return false;
return true;
}
void Init()
{
OutMap();
do {
Input();
} while (!Check());
}
void InitScore()
{
for (double & si : score)si = 0;
for (auto vi : vm) {
for (int j = 0; j < vi.size(); j++) {
score[vi[j]] += vi.size() - j;
}
}
}
void PageRank()
{
vector<double>newScore(NC);
for (auto vi : vm) {
double s = 0;
for (int j = vi.size() - 1; j >= 0; j--) {
newScore[vi[j]] += s, s += score[vi[j]];
}
}
score = newScore;
}
template<typename T>
vector<int> sortId(vector<T>v);
void GetScore()
{
vector<int>id = sortId(score);
for (auto i : id) {
if(avail[i])cout << vc[i] << " ";
}
cout << endl;
}
int main()
{
Init();
InitScore();
GetScore();
for (int i = 0; i < 5; i++) {
PageRank();
GetScore();
}
return 0;
}输出:
紫色 绿色 蓝色 翠绿 黄色 红色 棕色
紫色 蓝色 绿色 翠绿 黄色 红色 棕色
紫色 蓝色 绿色 黄色 翠绿 红色 棕色
紫色 蓝色 绿色 黄色 翠绿 红色 棕色
紫色 蓝色 绿色 黄色 翠绿 红色 棕色
紫色 蓝色 绿色 黄色 翠绿 红色 棕色
所以这一关的两个关键颜色就是紫色和蓝色。
3,ABAB模型
如果两个试管的上面两个元素都是上A下B,那么我们就有很大的理由相信A是关键颜色,也有一定理由相信B的二级关键颜色。
如上第64关,黄色和棕色就是ABAB模型。
又如第71关,有大量的ABAB模型:
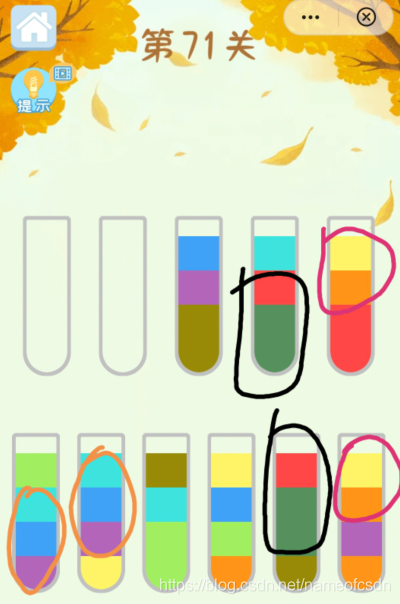
4,ABCA模型
如果一个试管的上面是上A下B,另外一个试管的上面是上C下A,那么我们就赋予C相对常规模型来说更高的自由度。
因为,C倒出去之后,2个A就可以合并了,B也能倒出去了。
更进一步,如果B有较高的自由度,我们就赋予C相对常规模型来说更高的自由度。
如第13关的黄色元素:

5,ABBA模型(循环压制模型)
如果一个试管的上面是上A下B,另外一个试管的上面是上B下A,那么我们相信,A和B至少有一个要赋予更高的自由度。
如第57关:

更一般的,n(n>1)个颜色的元素,都可以构成循环压制。
七,单点处理策略——死锁识别
有些状态已经是死亡状态了,如果能早点识别出来,就不用再往下尝试了。
死亡状态中,一个很有用的模型是死锁模型。
死锁又分为两种:循环压制死锁、单色压制死锁
1,循环压制死锁
最简单的循环压制死锁就是2个试管,即上文ABAB模型
循环压制死锁是不可能后期产生的,只能是开局自带的。
2,单色压制死锁
最简单的单色压制死锁就是2个试管,每个试管的最上面都是元素A,每个试管中A的下面至少还有一个颜色的其他元素,
这样,因为空间不够,就无法把A移动到同一个试管中,那么这些试管就无法进行任何操作,除非有别的试管参与进来。
3,死锁组合
如果若干个试管形成死锁,那么至少需要一个别的试管,才能完成水排序。
如果所有试管都没有空位,而且形成1个或若干个互不相关的死锁,那么显然这就已经成了死亡状态。(互不相关指的是没有共同颜色的元素,如下如第53关)
如第53关:

这就是2个死锁。
PS:死锁不一定是每个颜色都被另外一个颜色压制形成循环依赖,也有可能是如上这种,虽然没有被压制,但是没有足够的操作空间。
其实这2个死锁可以拆开来看,单是黄色元素所在的2个试管,就构成了死锁,于是黄色元素下面的橙色和蓝色元素也无法操作了。
还有非常复杂的死锁模型:

八,终极形态
1,终极形态
通过72关之后,就解锁了每日挑战。

而从第72关开始所有的偶数关卡,和所有的每日挑战,都进入了终极形态:14个试管,12个颜色。
除了试管新增3个,颜色新增3个,其他规则并没有变化。
2,图谱、算法求解
既然进入了终极形态,那就干脆做个图谱吧,方便描述。
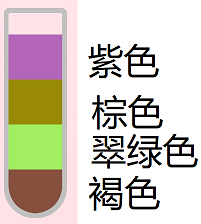
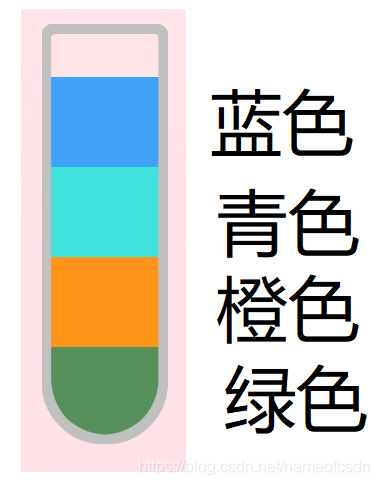
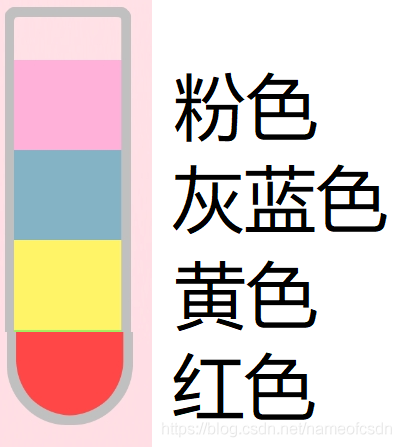
相应的,终极形态的代码也需要修改2行
#define NC 12
vector<string>vc = { "黄色","绿色","翠绿","青色","蓝色","紫色","棕色","橙色","红色" ,"灰蓝","褐色","粉色"};3,终极形态的策略
本质上来讲,规则并没有变化,策略也没有变化。
让我自己都有些意外的是,终极形态的策略,刚好就是上面所有策略的组合运用。
以第72关为例,首先是关键颜色,不难发现是橙色。
把棕色倒入空试管,然后把能移动的先移动下,得到:

黄色,蓝色,褐色构成循环压制,利用空试管可以解开,得到:

翠绿和棕色的循环压制,解开,得到:

同理,依次解开循环压制:



到最后就没什么难度了。
4,终极形态的策略总结
相对于前面试管较少的关卡,终极形态的策略中,上文的全局策略的重要性提高了很多。
整个破解的节奏,基本上都是需要完整的算好,经过一系列操作之后,空试管还在,这样才有必要试一试,而且这还仅仅是试一试,一直有空试管也不保证处于好的状态,可能已经处于死亡状态了但是看不出来。
前面试管较少的关卡,大部分时候如果一个颜色的所有元素都在各试管最上面,这个时候又有个空试管,那么就直接把这个颜色全部移到空试管内即可,
但是对于终极形态,如果因为把一个颜色移到一起,而丢失了空试管,没法迅速挪出一个空试管,那么就会直接卡死。
终极形态的玩法,就是凭借敏锐的直觉和强大的计算力,从一个含有空试管的状态,跳到下一个含有空试管的状态,比较难的关卡这之间有10步甚至更多。
5,难关——第100关

我试了好多次都还是差一点:

很明显,最麻烦的就是红色,其次就是粉色。
利用下文的DFS求解,轻轻松松得到答案。
输入:
14
-1 -1 -1 -1
-1 -1 -1 -1
9 3 4 5
7 6 1 8
3 0 7 6
5 3 0 5
8 11 1 1
11 4 10 8
10 11 9 11
2 3 4 9
2 0 4 2
6 10 5 8
7 1 0 2
9 10 6 7
输出:
deep = 45 from 12 to 0
deep = 44 from 7 to 10
deep = 43 from 10 to 3
deep = 42 from 10 to 0
deep = 41 from 0 to 7
deep = 40 from 10 to 0
deep = 39 from 0 to 9
deep = 38 from 9 to 3
deep = 37 from 3 to 9
deep = 36 from 9 to 2
deep = 35 from 9 to 7
deep = 34 from 7 to 11
deep = 33 from 7 to 1
deep = 32 from 7 to 3
deep = 31 from 3 to 13
deep = 30 from 13 to 4
deep = 29 from 4 to 3
deep = 28 from 3 to 11
deep = 27 from 11 to 5
deep = 26 from 5 to 12
deep = 25 from 12 to 6
deep = 24 from 6 to 8
deep = 23 from 6 to 3
deep = 22 from 3 to 12
deep = 21 from 12 to 4
deep = 20 from 3 to 13
deep = 19 from 3 to 4
deep = 18 from 4 to 5
deep = 17 from 5 to 2
deep = 16 from 4 to 2
deep = 15 from 2 to 11
deep = 14 from 11 to 1
deep = 13 from 11 to 13
deep = 12 from 13 to 1
deep = 11 from 1 to 8
deep = 10 from 8 to 0
deep = 9 from 0 to 8
deep = 8 from 8 to 1
deep = 7 from 1 to 5
deep = 6 from 5 to 2
deep = 5 from 2 to 7
deep = 4 from 7 to 8
deep = 3 from 8 to 13
deep = 2 from 13 to 0
deep = 1 from 2 to 1
deep = 0 from 2 to 0
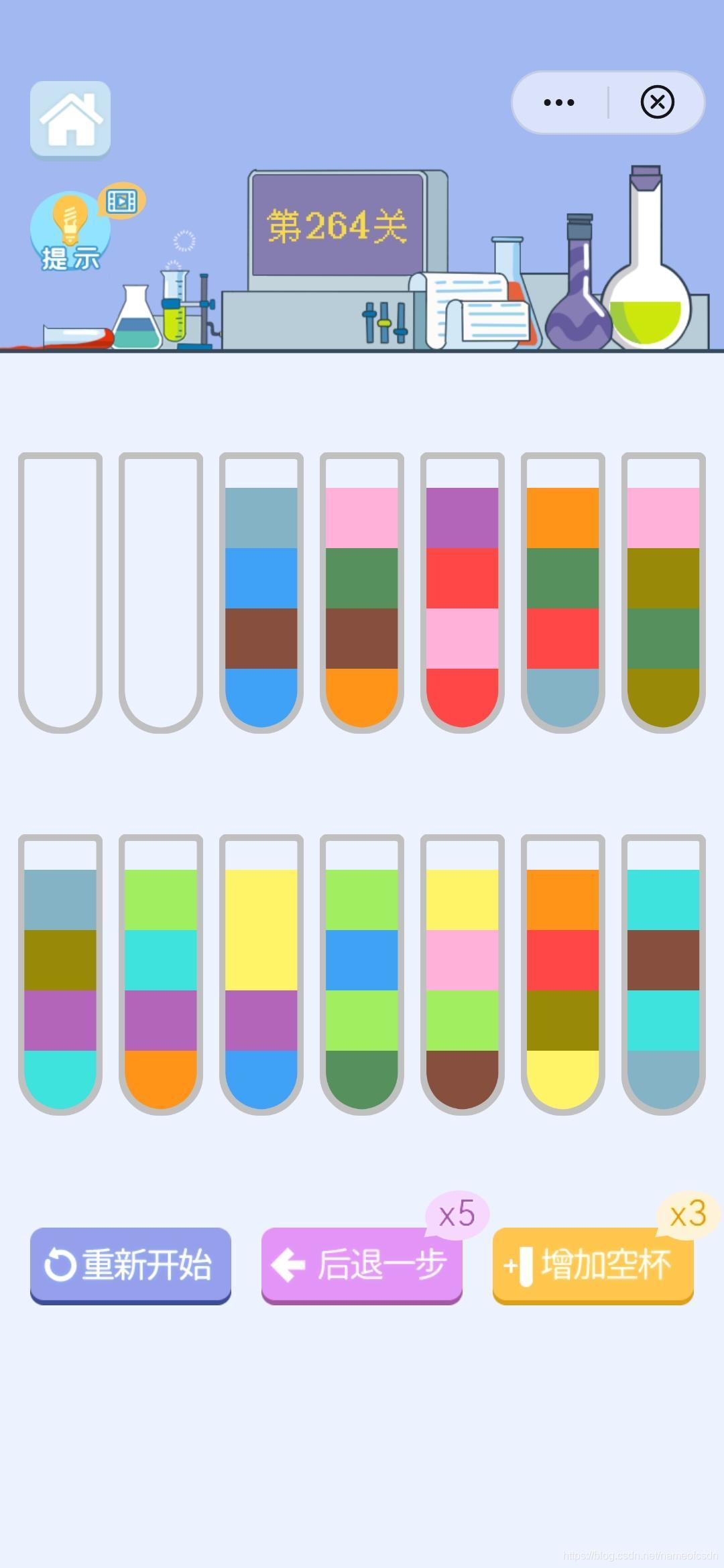
6,主线推关
2021年8月1日,主线关卡推到264关,不想继续玩了,没意思了,只剩重复的工作了。
九,每日挑战
1,1月挑战
1.1 - 1.2关卡基本上和第72关卡差不多。
1.3关卡稍微有些变化,开局就是四个颜色的循环压制:
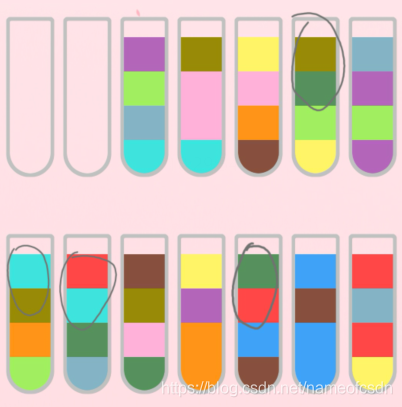
关键色肯定是从这里面出了,很明显,棕色或者红色是最好的选择。
这2个我都试过,红色是可以的,棕色应该不行。
到后面越来越难,也出现了越来越复杂的循环压制模型,
如1.28关卡:


如第1.29关:
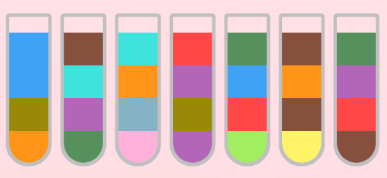

在我对象和我的强强联手下,大部分关卡都能在几分钟之内破解。
2,2月挑战
第2.4关比较难:

还有2.27关也很难:

试过用前面的算法去求解,看能不能辅助找到关键颜色:
12 4
7 3 1 6
4 0 10 8
8 7 1 9
10 3 11 1
9 0 8 5
3 11 2 4
6 11 11 0
5 6 10 7
1 3 4 2
2 7 5 0
6 4 10 5
9 8 2 9
不过并没有什么帮助,最终还是凭着多次尝试才找到了答案:
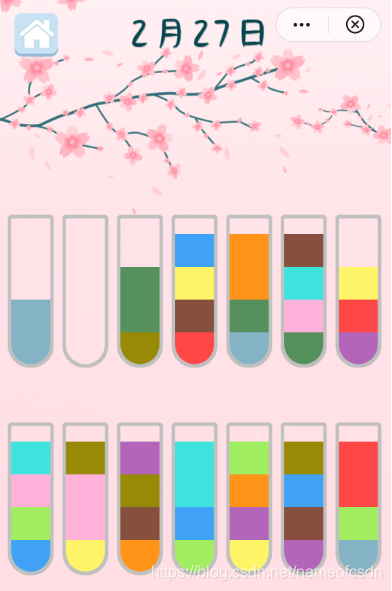
然后一共经过15步才能到达下一个含有空试管的状态:


到了这一步之后就没什么难度了。
3,3月挑战
首先一个比较难的关卡就是3.4关卡:
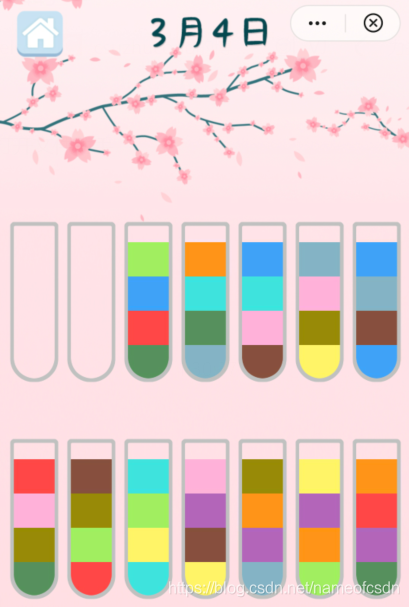
很明显,比较麻烦的就是绿色,情况和第100关差不多。
我能玩到这个状态:
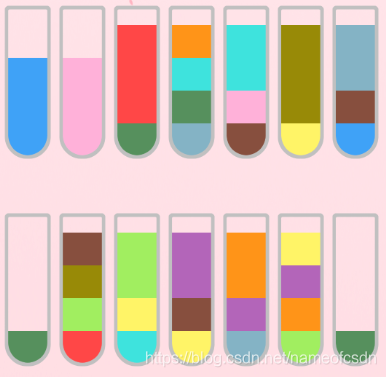
但是还是没有破解。
我利用下文的算法求解,其中的关键中间状态是这样的:

留下此图供参考,下次再有类似关卡再试试是不是能直接借鉴,进而完善我的启发式策略。
其他关卡就没什么难度了。
4,4月-7月挑战
4月没有特别难的关卡了,可能有些同等难度的关卡,因为遇到过,也不觉得那么难了。
5月比较难也比较有趣的就是第一天的关卡。
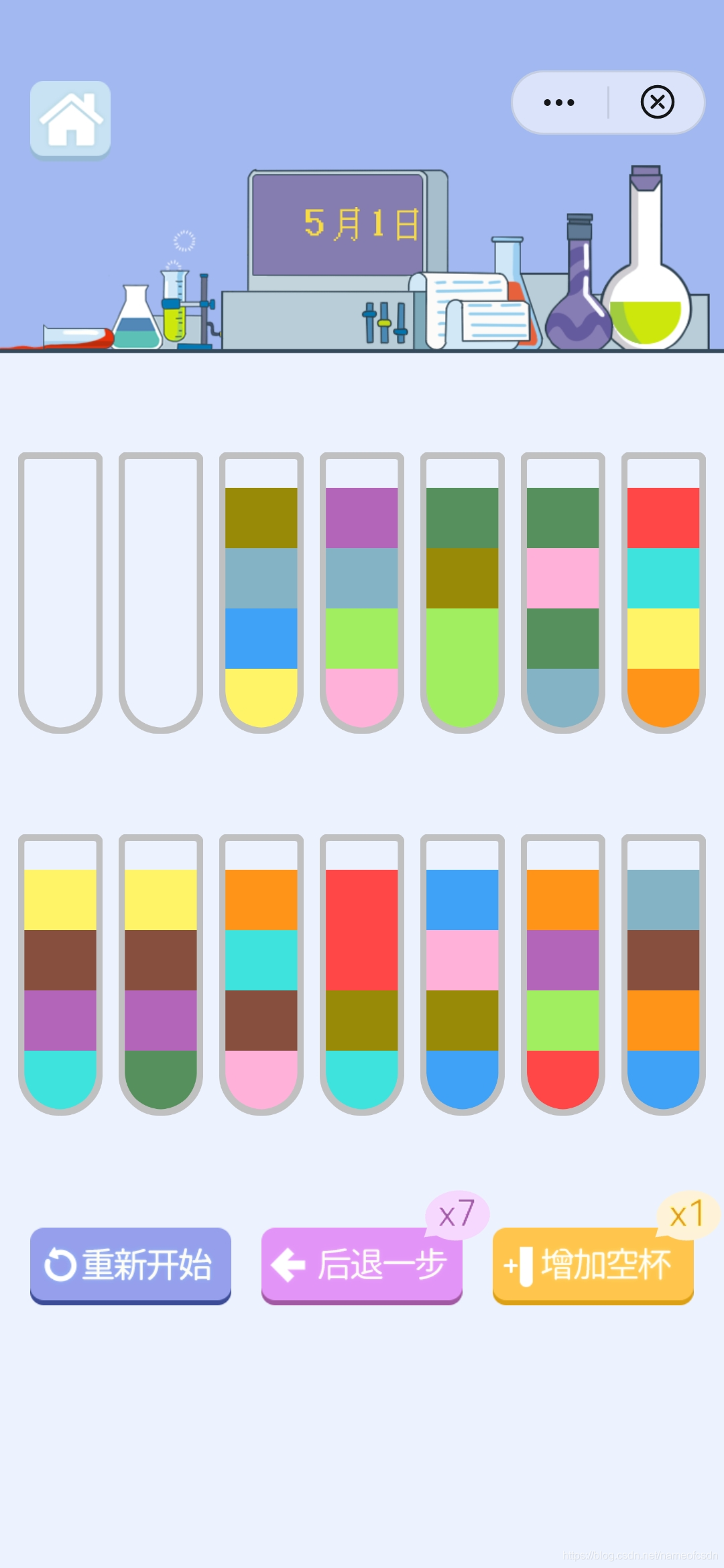
6月30日当天,刚好把直到当天的所有每日挑战全部通关。

后面更不会有什么觉得难的关卡了,直接熟能生巧了。

8月1日完成了7月挑战,决定弃游了。
十,DFS求解
1,思路
DFS的思路非常自然,就是能倒的就倒,不能倒的时候说明已经挂了,往上回溯即可。
回溯操作很简单,只需要记录最后一步倒的时候倒了几个单位的水即可,回溯的时候再把这几个单位放回去即可。
如果递归深度太深,容易造成栈溢出,所以我添加了阈值,当深度达到阈值时就算成功。
除了输出每一步的操作之外,我还输出了结果状态,直接复制下来,重新运行程序输入,即可接力搜索,我把这个创意叫接力搜索机制。
2,代码
DFS求解代码V1.0
#include<iostream>
#include<string>
#include<vector>
#include<algorithm>
#include<map>
using namespace std;
#define NC 12
#define SIZE 4
vector<string>vc = { "黄色","绿色","翠绿","青色","蓝色","紫色","棕色","橙色","红色" ,"灰蓝","褐色","粉色" };
vector<vector<int>>vm; //试管
int avail[NC]; //各色出现次数
map<vector<vector<int>>,int>visit;
void OutMap()
{
for (int i = 0; i < vc.size(); i++)
{
cout << i << " " << vc[i] << " ";
}
}
void Input()
{
int a;
cout << "\n输入总试管数目";
cin >> a;
vm.resize(a);
cout << "依次输入各试管内颜色,从上往下,空的用-1补足\n";
for (auto& vi : vm) {
for (int j = SIZE - 1; j >= 0; j--) {
cin >> a;
if (a == -1)continue;
vi.insert(vi.begin(),a), avail[a]++;
}
}
}
bool Check()
{
for (int i = 0; i < NC; i++)if (avail[i] != 0 && avail[i] != SIZE)return false;
return true;
}
void Init()
{
OutMap();
do {
Input();
} while (!Check());
}
bool oneCol(vector<int>&vi) //是否纯色
{
for (int i = 1; i < vi.size(); i++)if (vi[i] != vi[i - 1])return false;
return true;
}
bool end()
{
for (auto &vi : vm) if (!oneCol(vi))return false;
return true;
}
bool canPour(int i, int j) //i能否倒给j
{
if (i == j)return false;
int si = vm[i].size(), sj = vm[j].size();
if (si == 0 || sj == SIZE)return false;
if (sj == 0) { // 排除纯色元素倒入空试管的情况
return !oneCol(vm[i]);
}
int ci = vm[i][si - 1], cj = vm[j][sj - 1];
if (ci != cj)return false;
int num = 0;
for (int k = si - 1; k >= 0; k--)if (vm[i][k] == ci)num++;
return sj + num <= SIZE; // 加了同色必须倒完的限制,提高搜索效率
}
int pour(int i, int j) //返回倒了几个
{
int x = 0;
while (canPour(i, j)) {
auto it = vm[i].end() - 1;
vm[j].emplace_back(*it);
vm[i].erase(it);
x++;
}
return x;
}
void pour_f(int i, int j, int num) //按照数目回溯
{
while (num--) {
auto it = vm[i].end() - 1;
vm[j].emplace_back(*it);
vm[i].erase(it);
}
}
bool dfs(int deep)
{
if (visit.find(vm) != visit.end())return false;
visit[vm] = 1;
if (end() || deep>40) {
return true;
}
for (int i = 0; i < vm.size(); i++) {
for (int j = 0; j < vm.size(); j++) {
if (!canPour(i, j))continue;
if (i == 8 && j == 3 && deep==3) {
cout << 123;
}
int x = pour(i, j);
if (dfs(deep+1)) {
cout << "\ndeep = "<<deep<<" from " << i << " to " << j;
return true;
}
pour_f(j, i, x);
}
}
return false;
}
void outVm()
{
cout << endl;
for (auto vi : vm) {
int si = vi.size();
for (int i = SIZE - 1; i >= 0; i--) {
if (i >= si)cout << "-1 ";
else cout << vi[i] << " ";
}
}
}
int main()
{
Init();
dfs(0);
outVm();
return 0;
}
3,算法优缺点
优点:采用了一些剪枝策略,效率还是比较高的
缺点:加了同色必须倒完的限制,可能有一种有必要的操作我的算法无法进行,
如下图,把左边的灰蓝倒入右边2个试管。
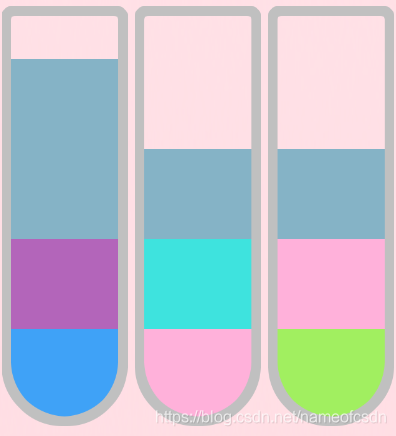
这种场景也是唯一的,有可能有必要,但是我的算法无法进行的操作。
就在我写了这个缺点分析后三天之内,我就遇到了必须使用这种操作的场景。
当然,这仍然无法说明从起始状态到最终状态必须要有这个操作,有可能只是某个中间状态到目标状态需要这个操作。
4,实战
以上面的第2.27关为例,运行输入:
14
-1 -1 -1 -1
-1 -1 -1 -1
7 3 1 6
4 0 10 8
8 7 1 9
10 3 11 1
9 0 8 5
3 11 2 4
6 11 11 0
5 6 10 7
1 3 4 2
2 7 5 0
6 4 10 5
9 8 2 9
输出:

按照这个操作得到:

如果把阈值改成50,直接一口气就能从头到尾全部算出来。

按照这个操作,直接就能得到:

因为每个试管都是纯色的,所以在我的算法中就是最终状态了。
5,BUG修复
经热心道友提醒,canPour函数有BUG,需要新增一行
bool canPour(int i, int j) //i能否倒给j
{
if (i == j)return false;
int si = vm[i].size(), sj = vm[j].size();
if (si == 0 || sj == SIZE)return false;
if (sj == 0) { // 排除纯色元素倒入空试管的情况
return !oneCol(vm[i]);
}
int ci = vm[i][si - 1], cj = vm[j][sj - 1];
if (ci != cj)return false;
int num = 0;
for (int k = si - 1; k >= 0; k--)if (vm[i][k] == ci)num++;
else break; // 修复BUG,新增一行
return sj + num <= SIZE; // 加了同色必须倒完的限制,提高搜索效率
}十一,Opencv求解
用Opencv直接读取图片,就不需要手动输入任何数据了。