计算机图形学——向量间的关系
向量点积(内积)
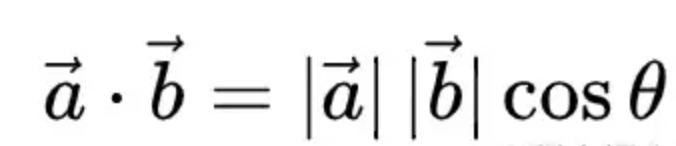
假设向量 a 为 (x, y), 向量 b 为 (x2, y2),则 a · b 为 x * x2 + y * y2 。
用来计算两个向量之间的夹角,但是无法区分向量的位置关系,因为反余弦函数arccos的范围是[0, 180]
向量叉乘
二维叉乘
设两个向量分别为 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_{1},y_{1}),(x_{2},y_{2}) (x1,y1),(x2,y2),那么它们的叉乘就为 ( x 1 ∗ y 2 − x 2 ∗ y 1 ) (x_{1}*y_{2}-x_{2}*y_{1}) (x1∗y2−x2∗y1),它也是一个向量。
几何意义:叉乘的几何意义是以两向量为邻边的平行四边形的有向面积。另外,根据右手规则,另外,定义向量 a ⃗ \vec{a} a、 b ⃗ \vec{b} b,当 a ⃗ X b ⃗ < 0 \vec{a}X\vec{b}<0 aXb<0时(X就表示叉乘), b ⃗ \vec{b} b对应的线段在 a ⃗ \vec{a} a的顺时针方向;当\vec{a}X\vec{b}=0时,\vec{a}、\vec{b}共线;当 a ⃗ X b ⃗ > 0 \vec{a}X\vec{b}>0 aXb>0时, b ⃗ \vec{b} b在 a ⃗ \vec{a} a的逆时针方向。(注意: a ⃗ X b ⃗ = − b ⃗ X a ⃗ \vec{a}X\vec{b}=-\vec{b}X\vec{a} aXb=−bXa,因此判断时要注意顺序)
三维叉乘
对于向量a 和 b
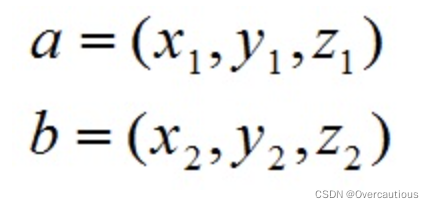
叉乘公式为:
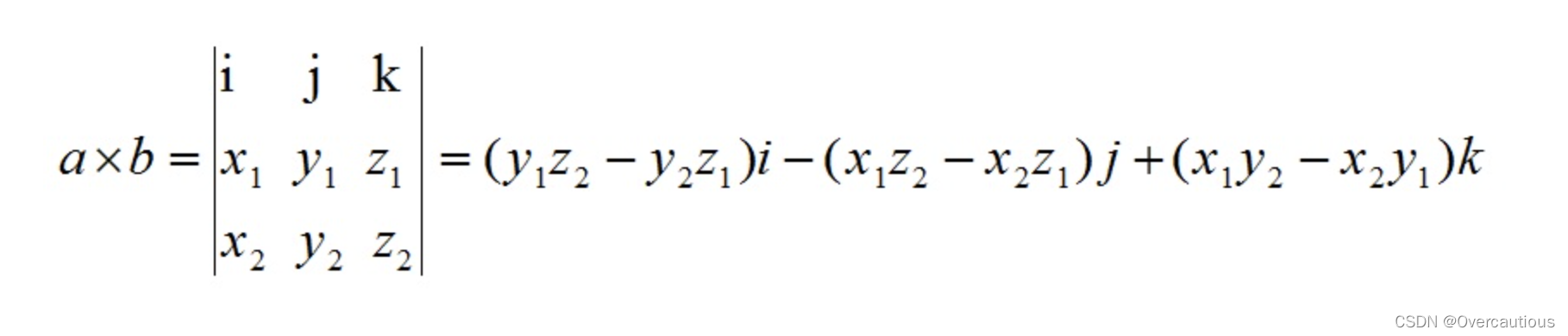
几何意义:在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。