Day52 树状数组线段树（lazy标记）

动态求连续区间和
树状数组是利用lowbit的性质求前缀和

lowbit(x)= $2^{k}$ ,k的意思是x的二进制表达最后面有几位0
然后c[x]是对 $x-2^{k},x]$ 范围内的q求和
然后修改，询问区间和都用到这个性质

#include<vector>
#include<cstring>
#include<cstdio>
#include<iostream>
#include<string>
#include<map>
#include<queue>
#include<algorithm>
#include<ctime>
#include<cmath>
#include<cstdlib>
#define lson (o<<1)
#define rson (o<<1|1)
#define fi first
#define sc second
#define dbg(x) cout<<#x<<" = "<<(x)<<endl;
#define rg register
typedef long long ll;
typedef unsigned int uint;
typedef unsigned long long ull;
using namespace std;
const double pi=acos(-1);
const double eps=1e-6;
inline int lowbit(int x){return x&(-x);}

template<typename A,typename B,typename C> inline A fpow(A x,B p,C yql){
	A ans=1;
	for(;p;p>>=1,x=1LL*x*x%yql)if(p&1)ans=1LL*x*ans%yql;
	return ans;
}


inline int read()
{
    int X=0,w=1;
    char c=getchar();
    while(c<'0'||c>'9')
    {
        if (c=='-')
        {
            w=-1;
        }
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        X=(X<<3)+(X<<1)+(c^48);
        c=getchar();
    }
    return X*w;
}
//inline void w(int x) { if(x>9) w(x/10); putchar(x%10+'0'); }
const int N=1e5+10; 
ll T;
int q[N],c[N],n,m;
#define lowbit(x) (x&-x)

void add(int a,int b){
	for(int i=a;i<=n;i+=lowbit(i)){
		c[i]+=b;
	}
}
int getsum(int a){
	int res=0;
	for(int i=a;i;i-=lowbit(i)){
		res+=c[i];
	}
	return res;
}
void solve(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>q[i];
		add(i,q[i]);
	}
	int op,a,b;
	for(int i=0;i<m;i++){
		cin>>op>>a>>b;
		if(op==0){
			cout<<getsum(b)-getsum(a-1)<<endl;
		}else {
			add(a,b);
		}
	}
}


int main(){
	std::ios::sync_with_stdio(0);
	std::cin.tie(0);
	T=1;
	//cin>>T;
	while(T--){
		solve();
	}
	return 0;
}

数星星
注意增加星星的时候是增加在32000范围内的星星
所以add的范围扩大到32000

然后要注意y是递增输入的
所以可以直接一行一行的增加我们的树状数组

#include<vector>
#include<cstring>
#include<cstdio>
#include<iostream>
#include<string>
#include<map>
#include<queue>
#include<algorithm>
#include<ctime>
#include<cmath>
#include<cstdlib>
#define lson (o<<1)
#define rson (o<<1|1)
#define fi first
#define sc second
#define dbg(x) cout<<#x<<" = "<<(x)<<endl;
#define rg register
typedef long long ll;
typedef unsigned int uint;
typedef unsigned long long ull;
using namespace std;
const double pi=acos(-1);
const double eps=1e-6;
inline int lowbit(int x){return x&(-x);}

template<typename A,typename B,typename C> inline A fpow(A x,B p,C yql){
	A ans=1;
	for(;p;p>>=1,x=1LL*x*x%yql)if(p&1)ans=1LL*x*ans%yql;
	return ans;
}


inline int read()
{
    int X=0,w=1;
    char c=getchar();
    while(c<'0'||c>'9')
    {
        if (c=='-')
        {
            w=-1;
        }
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        X=(X<<3)+(X<<1)+(c^48);
        c=getchar();
    }
    return X*w;
}
//inline void w(int x) { if(x>9) w(x/10); putchar(x%10+'0'); }
const int N=32010;
ll T;
int q[N],level[N],n,ans[N];


void add(int a){
	for(int i=a;i<=N;i+=lowbit(i)){
		level[i]++;
	}
}

int getsum(int a){
	int res=0;
	for(int i=a;i;i-=lowbit(i)){
		res+=level[i];
	}
	return res;
}

void solve(){
	cin>>n;
	int x,y;
	for(int i=0;i<n;i++){
		cin>>x>>y;
		x++;
		ans[getsum(x)]++;
		add(x);

	} 
	
	for(int i=0;i<n;i++)cout<<ans[i]<<endl;
}
//01122

int main(){
	std::ios::sync_with_stdio(0);
	std::cin.tie(0);
	T=1;
	//cin>>T;
	while(T--){
		solve();
	}
	return 0;
}

线段树
下面是query中l和r不修改的原因
因为tr[u].l+tr[u].r>>1和区间毫无关系
甚至可能扩大查询区间
比如下面查询[1，3]
就会把3扩大成5
从而查询到45的结果
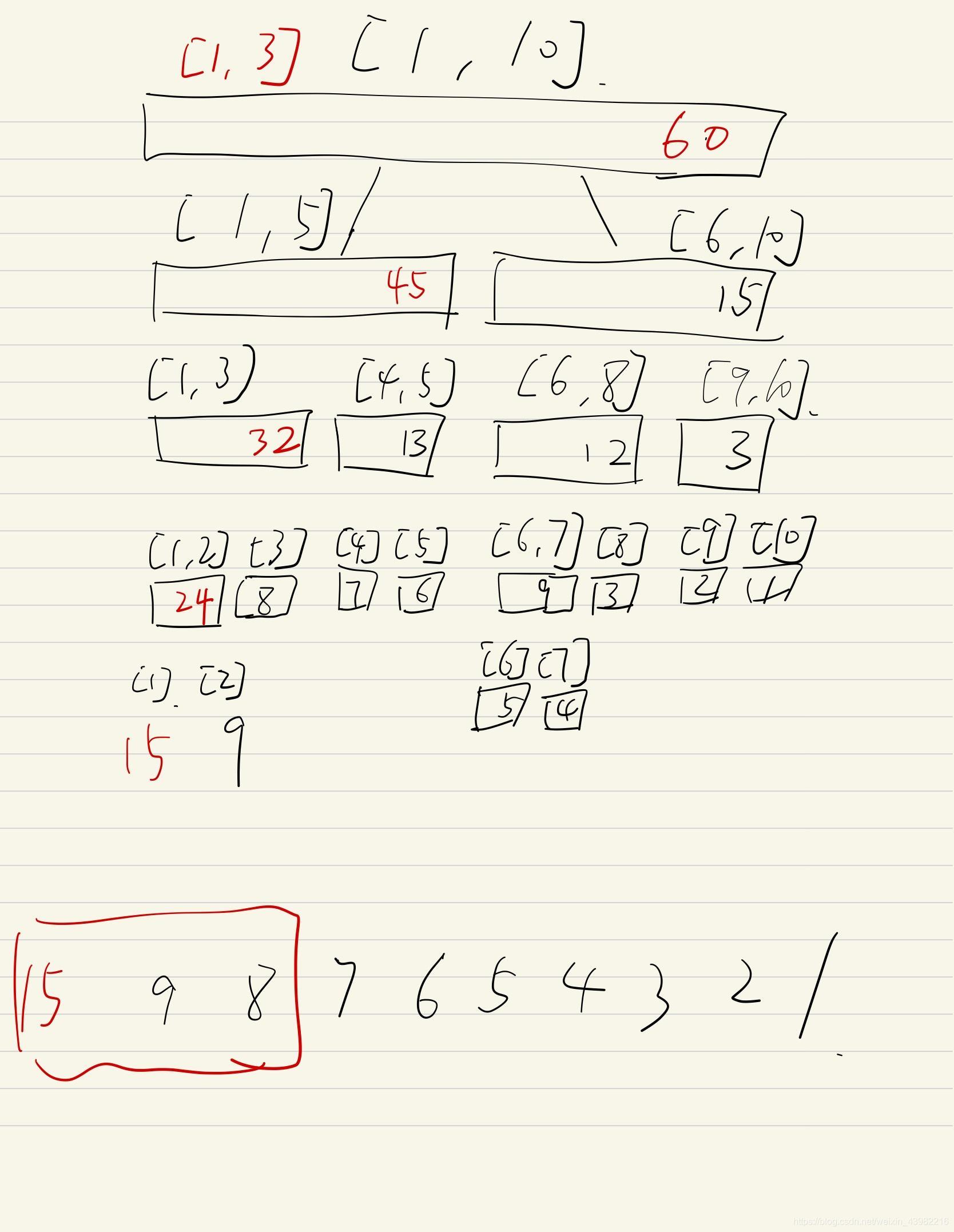
在这里插入图片描述
线段树

#include<vector>
#include<cstring>
#include<cstdio>
#include<iostream>
#include<string>
#include<map>
#include<queue>
#include<algorithm>
#include<ctime>
#include<cmath>
#include<cstdlib>
#define lson (o<<1)
#define rson (o<<1|1)
#define fi first
#define sc second
#define dbg(x) cout<<#x<<" = "<<(x)<<endl;
#define rg register
typedef long long ll;
typedef unsigned int uint;
typedef unsigned long long ull;
using namespace std;
const double pi=acos(-1);
const double eps=1e-6;
inline int lowbit(int x){return x&(-x);}

template<typename A,typename B,typename C> inline A fpow(A x,B p,C yql){
	A ans=1;
	for(;p;p>>=1,x=1LL*x*x%yql)if(p&1)ans=1LL*x*ans%yql;
	return ans;
}


inline int read()
{
    int X=0,w=1;
    char c=getchar();
    while(c<'0'||c>'9')
    {
        if (c=='-')
        {
            w=-1;
        }
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        X=(X<<3)+(X<<1)+(c^48);
        c=getchar();
    }
    return X*w;
}
//inline void w(int x) { if(x>9) w(x/10); putchar(x%10+'0'); }
const int N=1e5+10;
ll T;
struct node{
	int l,r,sum;
}tr[N*4];
int q[N];

void pushup(int u){
	tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
}

void build(int u,int l,int r){
	if(l==r){
		tr[u]={l,r,q[l]};
		return;
	}
	tr[u]={l,r};
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
	pushup(u);
}

int query(int u,int l,int r){
	if(tr[u].l>=l&&tr[u].r<=r){
		return tr[u].sum;
	}
	int mid=tr[u].l+tr[u].r>>1;
	int sum=0;
	if(l<=mid)sum=query(u<<1,l,r);
	if(r>mid)sum+=query(u<<1|1,l,r);
	return sum;
}

void add(int u,int x,int v){
	if(tr[u].l==tr[u].r){
		tr[u].sum+=v;
		return;
	}
	int mid=tr[u].l+tr[u].r>>1;
	if(x<=mid)add(u<<1,x,v);
	else add(u<<1|1,x,v);
	pushup(u);
	
}

void solve(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>q[i];
	}
	build(1,1,n);
	int op,a,b;
	for(int i=0;i<m;i++){
		cin>>op>>a>>b;
		if(op){
			add(1,a,b);
		}else{
			cout<<query(1,a,b)<<endl;
		}
	}
}


int main(){
	std::ios::sync_with_stdio(0);
	std::cin.tie(0);
	T=1;
	//cin>>T;
	while(T--){
		solve();
	}
	return 0;
}

lazy标记的线段树

#include<vector>
#include<cstring>
#include<cstdio>
#include<iostream>
#include<string>
#include<map>
#include<queue>
#include<algorithm>
#include<ctime>
#include<cmath>
#include<cstdlib>
#define lson (o<<1)
#define rson (o<<1|1)
#define fi first
#define sc second
#define dbg(x) cout<<#x<<" = "<<(x)<<endl;
#define rg register
typedef long long ll;
typedef unsigned int uint;
typedef unsigned long long ull;
using namespace std;
const double pi=acos(-1);
const double eps=1e-6;
inline int lowbit(int x){return x&(-x);}

template<typename A,typename B,typename C> inline A fpow(A x,B p,C yql){
	A ans=1;
	for(;p;p>>=1,x=1LL*x*x%yql)if(p&1)ans=1LL*x*ans%yql;
	return ans;
}


inline int read()
{
    int X=0,w=1;
    char c=getchar();
    while(c<'0'||c>'9')
    {
        if (c=='-')
        {
            w=-1;
        }
        c=getchar();
    }
    while(c>='0'&&c<='9')
    {
        X=(X<<3)+(X<<1)+(c^48);
        c=getchar();
    }
    return X*w;
}
//inline void w(int x) { if(x>9) w(x/10); putchar(x%10+'0'); }
const int N=1e5+10;
ll T;
struct node{
	int l,r;
	ll sum,add;
	#define l(x) tree[x].l
	#define r(x) tree[x].r
	#define sum(x) tree[x].sum
	#define add(x) tree[x].add
}tree[4*N];
ll q[N];

void build(int u,int l,int r){
	l(u)=l,r(u)=r;
	if(l==r){
		sum(u)=q[l];
		return;
	}
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
	sum(u)=sum(u<<1)+sum(u<<1|1);
}

void spread(int u){
	if(add(u)){
		sum(u<<1)+=add(u)*(r(u<<1)-l(u<<1)+1);
		sum(u<<1|1)+=add(u)*(r(u<<1|1)-l(u<<1|1)+1);
		add(u<<1)+=add(u);
		add(u<<1|1)+=add(u);
		add(u)=0;
	}
}

void change(int u,int l,int r,int v){
	if(l(u)>=l&&r(u)<=r){
		sum(u)+=(ll)v*(r(u)-l(u)+1);
		add(u)+=v;
		return;
	}
	spread(u); 
	int mid=l(u)+r(u)>>1;
	if(l<=mid)change(u<<1,l,r,v);
	if(r>mid)change(u<<1|1,l,r,v);
	sum(u)=sum(u<<1)+sum(u<<1|1);
}

ll query(int u,int l,int r){
	if(l(u)>=l&&r(u)<=r){
		return sum(u);
	}
	spread(u);
	int mid=l(u)+r(u)>>1;
	ll sum=0;
	if(l<=mid)sum+=query(u<<1,l,r);
	if(r>mid) sum+=query(u<<1|1,l,r);
	return sum;
}

void solve(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>q[i];
	build(1,1,n);
	int op,x,y;
	while(m--){
		cin>>op;
		if(op==1){
			cin>>x>>y;
			change(1,x,x,y);
		}else {
			cin>>x>>y;
			cout<<query(1,x,y)<<endl;
		//	query(1,x,y);
		}
	}
}


int main(){
	std::ios::sync_with_stdio(0);
	std::cin.tie(0);
	T=1;
	//cin>>T;
	while(T--){
		solve();
	}
	return 0;
}

最好把lson和rson封装

真的会写错。。。。

然后注意mid缩小范围只在build中出现
spread要在判断完边界后立刻执行