巴特沃斯(Butterworth)滤波器（一）

首先考虑一个归一化（截止频率为1rad/s）的低通滤波器,其幅频特性表达式如下：

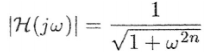
其幅频特性曲线如下图：

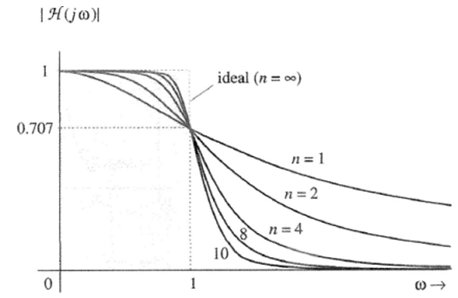
当n–> $\infty$ 时，得到一个理想的低通滤波器：
当w>1(截止频率)时，增益为0；
当w<1(截止频率)时，增益为1；
当w=1(截止频率)时，增益为0.707（衰减到-3dB）；

其次，我们根据上面的幅频特性表达式求滤波器传递函数

根据以下三个公式：

• s = jw
• ${\left|H_{(s)}\right|}^2=H_{(s)}\overline{H_{(s)}}$
• $H_{(-s)}=\overline{H_{(s)}}$

推导下：

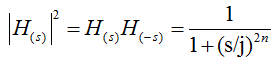
因此极点为：

下面是n=1到n=4阶的极点位置：

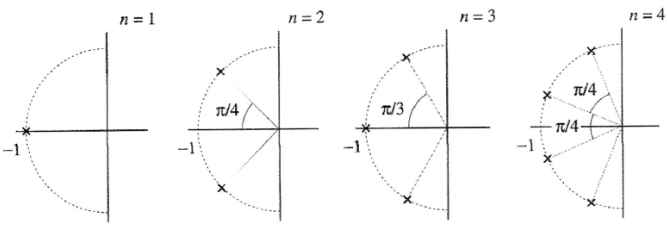
例如，四阶Butterworth低通滤波器的极点所在角度为：

这样 1到10阶的Butterworth多项式因子表格如下：

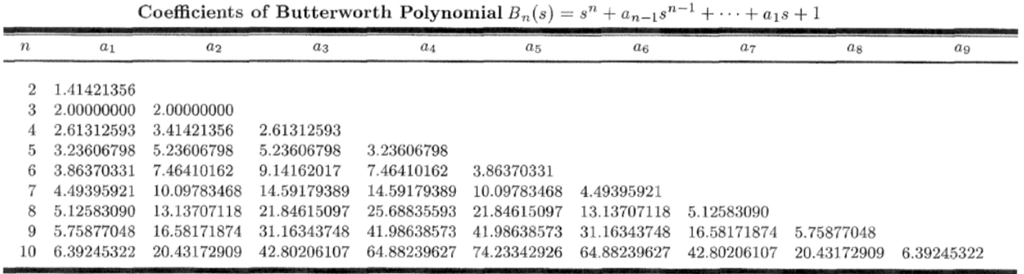
以上我们考虑的是截止频率为1的情况，其它截止频率可将传递函数中的s替换为：s/wc ,wc为截止频率，单位rad/s。例如二阶截止频率为100rad/s的传递函数为：

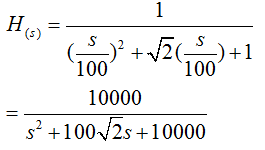
转载：https://www.cnblogs.com/xpvincent/p/5557659.html