乘法器的实现(阵列、Booth、Wallace)
文章目录
1 乘法器
M和N位宽输入的乘法,采用一个N加法器需要M个周期。
利用移位和相加将M个部分积(partial product)加在一起。部分积的计算位相乘本质上是与逻辑。
101010 被乘数
× 1011 乘数
———————————
101010 \
101010 | 部分积
000000 |
+ 101010 /
—————————————
111001110
2 部分积的产生
2.1 波兹(Booth)编码
乘数 8’b0111_1110 可以转换成 8’b1000_0000 - 8’b0000_0010 。这里用8’b1000_00I0 表示(I表示 -1 )。
这可以减少非0行的数量,使得部分积的数目至少可以减少原来的一半。部分积数目的减少意味着相加次数的减少,从而加快了运算速度并减少了面积。
保证了在每两个连续位中最多只有一个是 1 或者 -1 。形式上相当于把乘数变换成一个四进制形式。8’b1000_00I0 = (2,0,0,-2)(四进制)
问题:与{0,1}相乘等效于AND,但是与{-2,-1,0,1,2}相乘还需要反向逻辑和移位逻辑,大小不同的部分积阵列对乘法器设计不合理。
2.2 改进的波兹编码
改进的波兹编码(modified Booth’s recoding)乘数由最高有效位(msb)到最低有效位(lsb)进行,按3位一组进行划分,相互重叠一位,编码表:
| 乘数位 | 编码位 | 编码 |
|---|---|---|
| 000 | 0 | 00 |
| 001 | +被乘数 | 01 |
| 010 | +被乘数 | 01 |
| 011 | +2×被乘数 | 10 |
| 100 | -2×被乘数 | I0 |
| 101 | -被乘数 | 0I |
| 110 | -被乘数 | 0I |
| 111 | 0 | 00 |
本质是从msb到lsb检查乘数中1的字串,用一个以1开头或以-1结尾的字符串代替他们。
例子:
011 :一串1的开始,所以用一个开头的1代替(100)
110 :一串1的结尾,所以用一个结尾的-1代替(0I0)
8’b0111_1110,从msb到lsb,分成3位一组首尾重叠的4组:01(1),11(1),11(1),10(0)。编码后为10,00,00,I0,这与上述的编码是吻合的。
3 部分积的累加
对部分积相加是一个多操作数的加法,一个直接累加的部分积方法是用许多加法器形成阵列,所以被称为 阵列乘法器(array multiplier)。
一个更为先进的方法与树结构的形式完成加法。
3.1 阵列乘法器
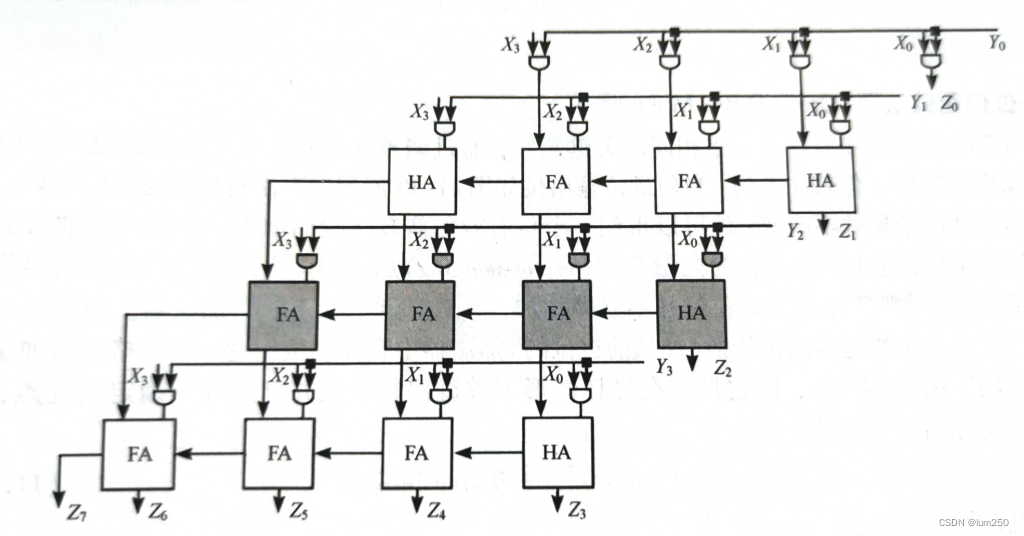
AND 门产生部分积,加法器阵列实现相加。

所有关键路径都具有相同的长度。
上述乘法器只能进行无符号数相乘。
3.2 进位保留乘法器
如果进位向下沿而不是向左,可以得到一个更有效的实现。进位不是立即相加,而是传递给下一级加法器,在最后一级在一个快速进位传播(如超前进位)加法器中合并。
代价:需要一个额外的加法器,被称为向量合并(vector-merging)加法器。由此得到的乘法器被称为进位保留乘法器。
优点:在最坏情形下关键路径最短且唯一确定。
拓扑优化后的结构:

这种结构可以更好的映射到硅片上。
3.3 Wallace 树形乘法器
部分积加法器可以设计成树形,可以减少关键路径和所需的加法器单元数目。
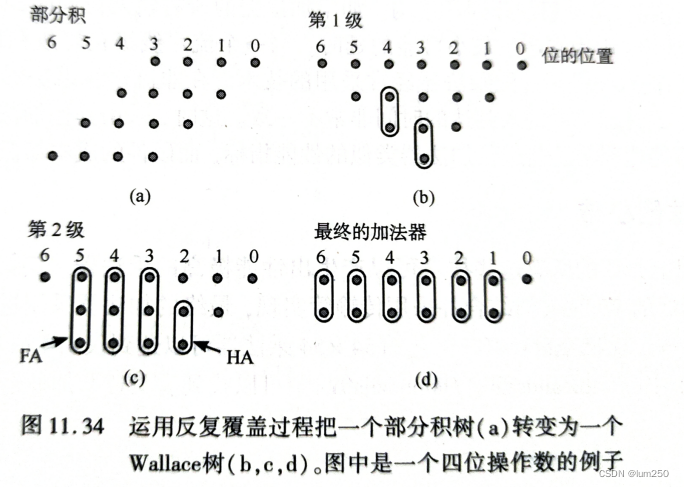
上面的4个4位部分积,只有第3bit需要加 4 个。
第一步,第3列和低4列引入2个半加器,如图b所示,压缩后得到图c。
第二步,第3、4、5列引入3个全加器,第2列引入1个半加器,得到图d。
第三步,使用简单的两输入加法器。
前两步一共使用了3个全加器、3个半加器。原来的进位保留乘法器结构需要6个全加器、6个半加器。
全加器3个输入两个输出,所以运算过程中又称为压缩器。
优点:
- 节省了较大乘法器所需硬件,减少了传播延时。
缺点:
- 不规则,高质量版图设计任务变复杂。
4 Verilog 实现
4.1 普通阵列乘法器
以 8bit 无符号数相乘为例,注意这里的设计没有考虑性能。
array_multiplier.v:
`timescale 1ns/1ps
module array_multiplier (
input I_sys_clk,
input I_reset_n,
input I_valid,
input [7:0] I_a,
input [7:0] I_b,
output reg O_valid,
output reg [15:0] O_c
);
//--- Main body of code ---
always @(posedge I_sys_clk or negedge I_reset_n)
begin
if(~I_reset_n)
begin
O_valid <= 1'b0;
O_c <= 16'b0;
end
else
begin
O_valid <= I_valid;
O_c <= (({8{I_b[0]}} & I_a) ) +
(({8{I_b[1]}} & I_a) << 1) +
(({8{I_b[2]}} & I_a) << 2) +
(({8{I_b[3]}} & I_a) << 3) +
(({8{I_b[4]}} & I_a) << 4) +
(({8{I_b[5]}} & I_a) << 5) +
(({8{I_b[6]}} & I_a) << 6) +
(({8{I_b[7]}} & I_a) << 7)
;
end
end
endmodule
testbench array_multiplier_tb.sv:
`timescale 1ns/1ps
module array_multiplier_tb();
parameter T = 5;
reg I_sys_clk;
reg I_reset_n;
reg I_valid ;
reg [7:0] I_a ;
reg [7:0] I_b ;
wire O_valid ;
wire [15:0] O_c ;
initial begin
I_sys_clk <= 'b0;
I_reset_n <= 'b0;
I_valid <= 'b0;
I_a <= 'b0;
I_b <= 'b0;
#(T*20)
I_reset_n <= 'b1;
#(T*20)
data_gen();
$finish();
end
always #(T/2) I_sys_clk <= ~I_sys_clk;
array_multiplier array_multiplier_u (
.I_sys_clk(I_sys_clk),
.I_reset_n(I_reset_n),
.I_valid (I_valid ),
.I_a (I_a ),
.I_b (I_b ),
.O_valid (O_valid ),
.O_c (O_c )
);
task data_gen();
for (int i = 0; i < 256; i++) begin
I_valid <= 'b1;
I_a <= i;
I_b <= i;
$display("%d x %d = %d", i, i, i*i);
@(posedge I_sys_clk);
I_valid <= 'b0;
end
endtask
endmodule
sim.do 文件:
cd D:/prj/modelsim_prj/multiplier/array_multiplier/
vlib work
vlog array_multiplier.v array_multiplier_tb.sv
vsim -novopt work.array_multiplier_tb
sim.bat 文件:
vsim -do sim.do
所有文件放在相同路径下,双击批处理文件即可开始Modelsim仿真。
仿真结果:
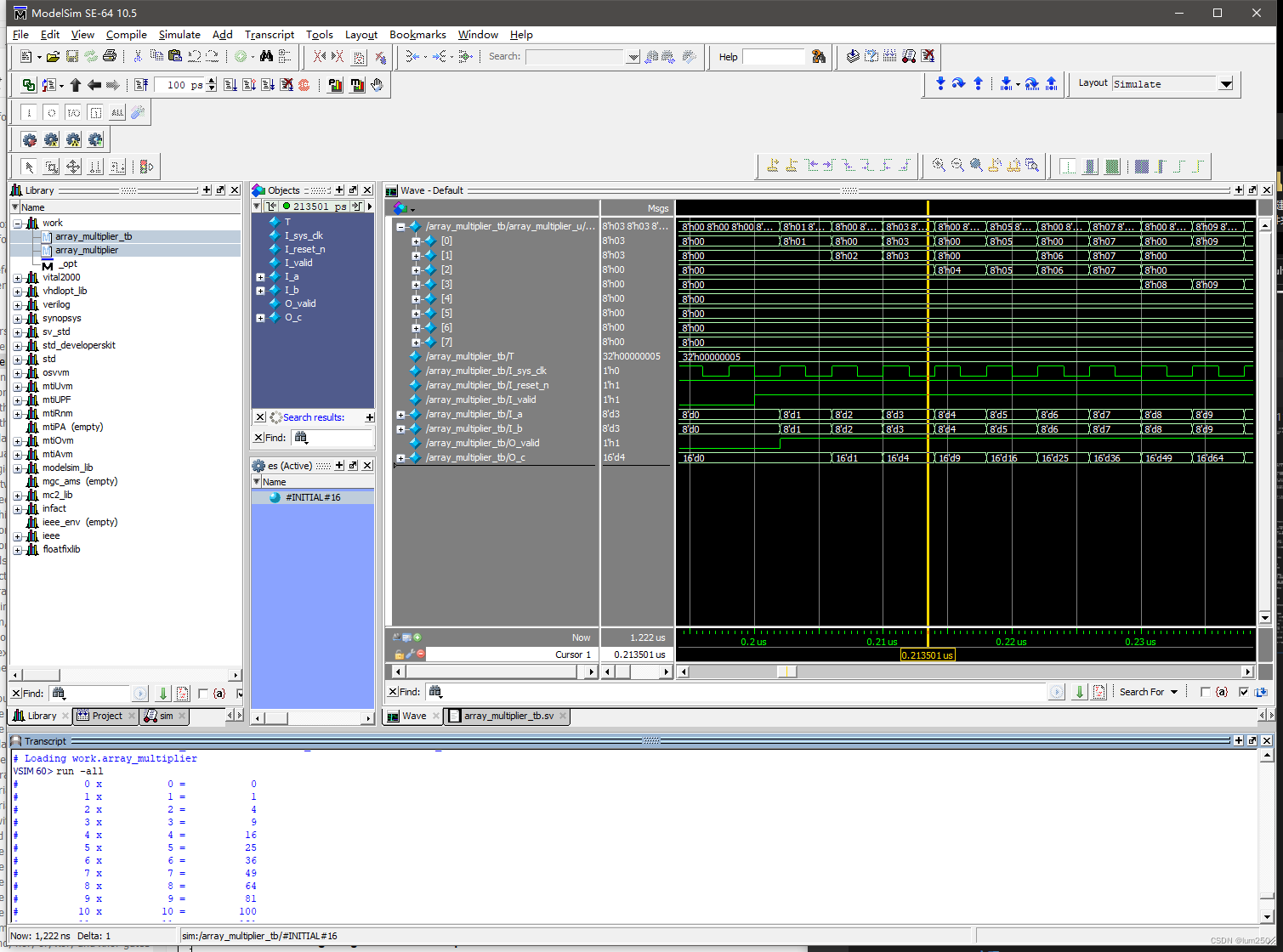
4.2 Booth 乘法器
Verilog 设计,注意,这个代码只是描述算法,需要进行符号位拓展、乘换成与逻辑、以及将乘2的幂转换为移位处理。
`timescale 1ns/1ps
module booth_multiplier (
input I_sys_clk,
input I_reset_n,
input I_valid ,
input [7:0] I_a ,
input [7:0] I_b ,
output reg O_valid ,
output reg [15:0] O_c
);
//--- Main body of code ---
wire [8:0] W_b;
wire [15:0] W_a_n;
wire [2:0] W_booth_code_pre [0:3];
reg R_valid ;
reg signed [15:0] R_partial_product [0:3];
assign W_b = {I_b, 1'b0};
assign W_a_n = -{{8{I_a[7]}}, I_a};
genvar gen_i;
for (gen_i = 0; gen_i < 4; gen_i = gen_i + 1) begin
assign W_booth_code_pre[gen_i] = W_b[gen_i*2 +: 3];
always @(posedge I_sys_clk or negedge I_reset_n)
begin
if(~I_reset_n)
begin
R_partial_product[gen_i] <= 1'b0;
end
else
begin
case (W_booth_code_pre[gen_i])
3'b000: R_partial_product[gen_i] <= 9'b0;
3'b001: R_partial_product[gen_i] <= $signed(I_a) * 1 * 2**(gen_i*2) ;
3'b010: R_partial_product[gen_i] <= $signed(I_a) * 1 * 2**(gen_i*2) ;
3'b011: R_partial_product[gen_i] <= $signed(I_a) * 2 * 2**(gen_i*2) ;
3'b100: R_partial_product[gen_i] <= $signed(I_a) * -2 * 2**(gen_i*2) ;
3'b101: R_partial_product[gen_i] <= $signed(I_a) * -1 * 2**(gen_i*2) ;
3'b110: R_partial_product[gen_i] <= $signed(I_a) * -1 * 2**(gen_i*2) ;
3'b111: R_partial_product[gen_i] <= 9'b0;
default: R_partial_product[gen_i] <= 9'b0;
endcase
end
end
end
always @(posedge I_sys_clk or negedge I_reset_n)
begin
if(~I_reset_n)
begin
R_valid <= 1'b0;
end
else
begin
R_valid <= I_valid;
end
end
always @(posedge I_sys_clk or negedge I_reset_n)
begin
if(~I_reset_n)
begin
O_valid <= 1'b0;
O_c <= 16'b0;
end
else
begin
O_valid <= R_valid;
O_c <= R_partial_product[0] +
R_partial_product[1] +
R_partial_product[2] +
R_partial_product[3]
;
end
end
endmodule
testchech:
`timescale 1ns/1ps
module booth_multiplier_tb();
parameter T = 5;
reg I_sys_clk;
reg I_reset_n;
reg I_valid ;
reg [7:0] I_a ;
reg [7:0] I_b ;
wire O_valid ;
wire [15:0] O_c ;
// reference model signal
reg [7:0] R_i ;
reg [7:0] R1_i ;
reg [7:0] R2_i ;
initial begin
I_sys_clk <= 'b0;
I_reset_n <= 'b0;
I_valid <= 'b0;
I_a <= 'b0;
I_b <= 'b0;
#(T*20)
I_reset_n <= 'b1;
#(T*20)
data_gen();
$finish();
end
always #(T/2) I_sys_clk <= ~I_sys_clk;
booth_multiplier booth_multiplier_u (
.I_sys_clk(I_sys_clk),
.I_reset_n(I_reset_n),
.I_valid (I_valid ),
.I_a (I_a ),
.I_b (I_b ),
.O_valid (O_valid ),
.O_c (O_c )
);
task data_gen();
for (int i = 0; i < 256; i++) begin
I_valid <= 'b1;
I_a <= i;
I_b <= i;
R_i <= i;
R1_i <= R_i;
R2_i <= R1_i;
// reference model
if (O_valid)
begin
$display("i=%d, O_c=%d, check=%d", $signed(R2_i), $signed(O_c), $signed(O_c) == $signed(R2_i) * $signed(R2_i));
end
@(posedge I_sys_clk);
I_valid <= 'b0;
end
endtask
endmodule
Modilsim do文件做对应修改,sim.do:
cd D:/prj/modelsim_prj/multiplier/booth_multiplier/
vlib work
vlog booth_multiplier.v booth_multiplier_tb.sv
vsim -novopt work.booth_multiplier_tb
仿真结果:

4.3 Wallace 乘法器
以4bit×4bit为例,按照结构把线连起来就行:
wallace_multiplier.v:
`timescale 1ns/1ps
module wallace_multiplier (
input I_sys_clk,
input I_reset_n,
input I_valid ,
input [3:0] I_a ,
input [3:0] I_b ,
output reg O_valid ,
output reg [7:0] O_c
);
reg R_valid ;
reg [3:0] R_partial_product [0:3];
wire [1:0] W_level1_c,W_level1_carry;
wire [3:0] W_level2_c,W_level2_carry;
wire [6:0] W_level3[0:1];
genvar gen_i;
generate
for (gen_i = 0; gen_i < 4; gen_i = gen_i + 1) begin
always @(posedge I_sys_clk or negedge I_reset_n)
begin
if(~I_reset_n)
begin
R_partial_product[gen_i] = 4'd0;
end
else
begin
R_partial_product[gen_i] = {4{I_b[gen_i]}} & I_a;
end
end
end
endgenerate
// level1
adder_half adder_half_u1 (
.I_a (R_partial_product[2][1]),
.I_b (R_partial_product[3][0]),
.O_c (W_level1_c[0]),
.O_carry(W_level1_carry[0])
);
adder_half adder_half_u2 (
.I_a (R_partial_product[1][3]),
.I_b (R_partial_product[2][2]),
.O_c (W_level1_c[1]),
.O_carry(W_level1_carry[1])
);
// level2
adder_half adder_half_u3 (
.I_a (R_partial_product[1][1]),
.I_b (R_partial_product[2][0]),
.O_c (W_level2_c[0] ),
.O_carry(W_level2_carry[0])
);
adder adder_u1 (
.I_a (R_partial_product[0][3]),
.I_b (R_partial_product[1][2]),
.I_carry (W_level1_c[0] ),
.O_c (W_level2_c[1] ),
.O_carry (W_level2_carry[1] )
);
adder adder_u2 (
.I_a (R_partial_product[1][3]),
.I_b (W_level1_c[1] ),
.I_carry (W_level1_carry[0] ),
.O_c (W_level2_c[2] ),
.O_carry (W_level2_carry[2] )
);
adder adder_u3 (
.I_a (R_partial_product[2][3]),
.I_b (R_partial_product[3][2]),
.I_carry (W_level1_carry[1] ),
.O_c (W_level2_c[3] ),
.O_carry (W_level2_carry[3] )
);
assign W_level3[0] = {R_partial_product[3][3], W_level2_c[3:1], R_partial_product[0][2:0]};
assign W_level3[1] = {W_level2_carry[3:0], W_level2_c[0], R_partial_product[1][0], 1'b0};
always @(posedge I_sys_clk or negedge I_reset_n)
begin
if(~I_reset_n)
begin
R_valid <= 1'b0;
O_valid <= 1'd0;
O_c <= 8'd0;
end
else
begin
R_valid <= I_valid;
O_valid <= R_valid;
O_c <= W_level3[0] + W_level3[1];
end
end
endmodule
module adder_half (
input I_a,
input I_b,
output O_c,
output O_carry
);
assign O_c = I_a ^ I_b;
assign O_carry = I_a & I_b;
endmodule
module adder (
input I_a,
input I_b,
input I_carry,
output O_c,
output O_carry
);
assign O_c = I_a ^ I_b ^ I_carry;
assign O_carry = (I_a & I_b) | ((I_a ^ I_b) & I_carry);
endmodule
仿真结果:
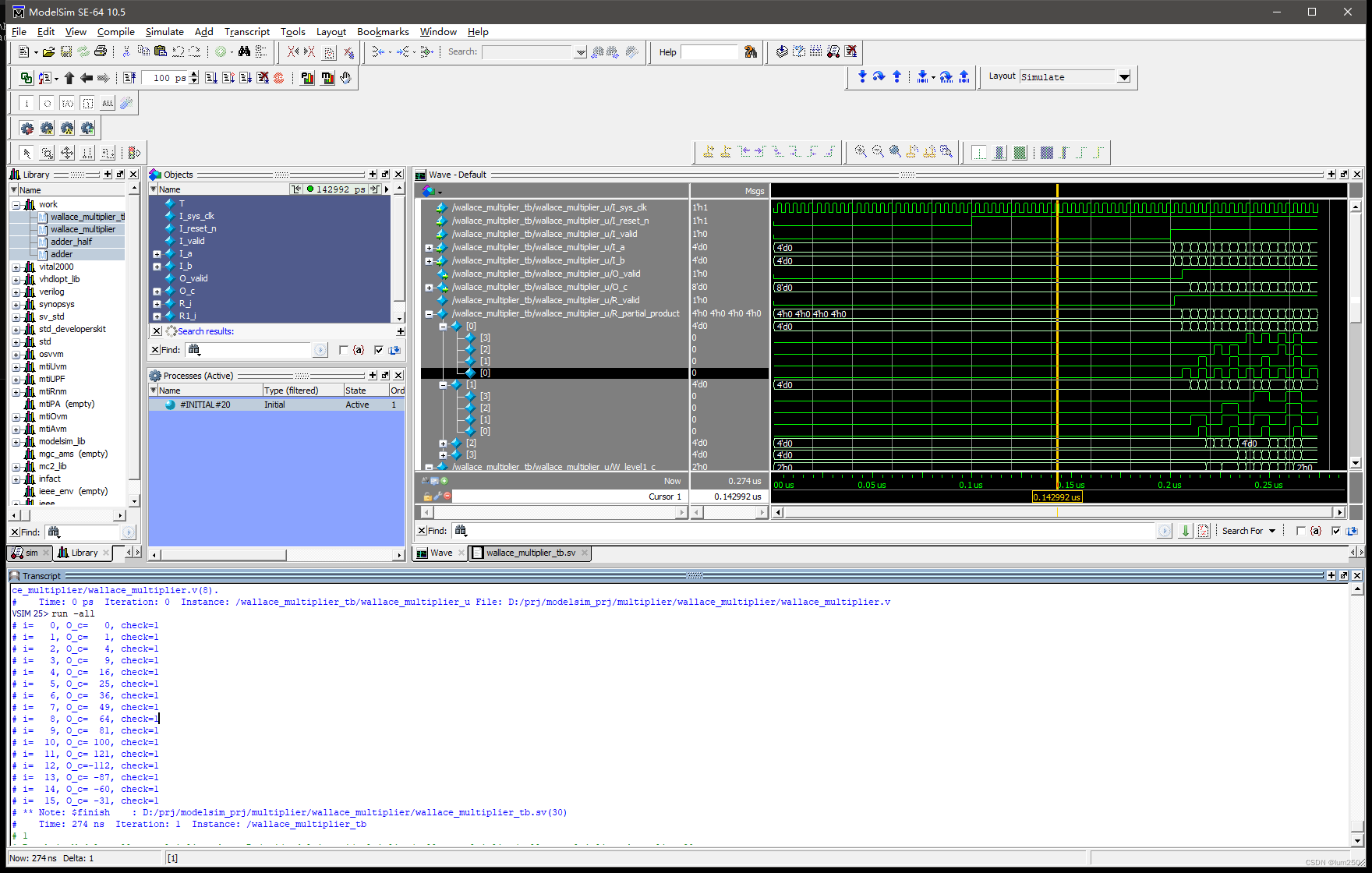
5 总结
数字集成电路设计可能对加法器的面积和版图有较高的要求。对于FPGA设计,可能基本阵列加法器用着还更简单顺手。主要看的的题目可能问的是与一个常数相乘的设计,这个时候要参考 Booth 编码的思想,因为不是实时乘数的话,预编码之后确实还是节省资源的。
参考
数字集成电路-电路、系统与设计(第二版)