LeetCode之贪心算法
文章目录
前言
打开LeetCode网站,如果我们按照题目类型数量分类,最多的几个题型有数组、动态规划、数学、字符串、树、哈希表、深度优先搜索、二分查找、贪心算法、广度优先搜索、双指针等待。
一、题目分类
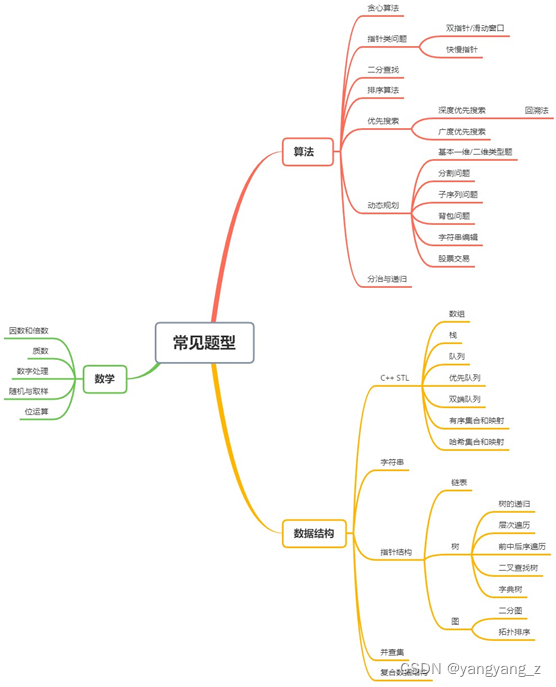
第一大分类是算法。本文先从最简单的贪心算法讲起,然后逐渐进阶到二分查找、排序算法和搜索算法,最后是难度比较高的动态规划和分治算法。
第二大分类是数学,包括偏向纯数学的数学问题,和偏向计算机知识的位运算问题。这类问题通常来测试是否敏锐,在实际工作中并不常用,可以优先把精力放在其他大类上。
第三大分类是数据结构,包括C++STL内包含的常见数据结构、字符串处理、链表、树和图。其中,链表、树、和图都是用指针表示的数据结构,且前者是后者的子集。最后我们也将介绍一些更复杂的数据结构,比如经典的并查集和LRU。
二、最易懂的贪心算法
内容提要:本小节包括算法解释 、区间问题、分配问题和练习。
2.1 算法解释
顾名思义,贪心算法和贪心思想采用贪心的策略,保证每次操作都是局部最优的,从而使最后得到的结果是全局最优的。
举一个最简单的例子:小明和小王喜欢吃苹果,小明可以吃五个,小王可以吃三个。已知苹果园里有吃不完的苹果,求小明和小王一共最多吃多少个苹果。在这个例子中,我们可以选用的贪心策略为,每个人吃自己能吃的最多数量的苹果,这在每个人身上都是局部最优的。又因为全局结果是局部结果的简单求和,且局部结果互不相干,因此局部最优的策略也同样是全局最优的策略。
2.2 分配问题
455. 分发饼干
【题目描述】有一群孩子和一堆饼干,每个孩子有一个饥饿度,每个饼干都有一个大小。每个孩子只能吃最多一个饼干,且只有饼干的大小大于孩子的饥饿度时,这个孩子才能吃饱。求解最多有多少孩子可以吃饱。
【题解】因为饥饿度最小的孩子最容易吃饱,所以我们先考虑这个孩子。为了尽量使得剩下的饼干可以满足饥饿度更大的孩子,所以我们应该把大于等于这个孩子饥饿度的、且大小最小的饼干给这个孩子。满足了这个孩子之后,我们采取同样的策略 ,考虑剩下孩子里饥饿度最下的孩子,直到没有满足条件的存在。
简言之,这里的贪心策略是,给剩余孩子里最小饥饿度的孩子分配最小的能饱腹的饼干。
至于具体实现,因为我们需要获得大小关系,一个便捷的方法就是把孩子和饼干分别排序。这样我们就可以从饥饿度最小的孩子和大小最小的饼干出发,计算有多少个对子可以满足条件。
- 注意 对数组或字符串排序是常见的操作,方便之后的大小比较
- 注意 在之后的讲解中,若我们谈论的是对连续空间的变量进行操作,我们并不会明确区分数组和字符串,因为他们本质上都是连续空间上的有序变量集合。一个字符串“abc”可以被看做一个数组[‘a’,‘b’,‘c’].
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
sort(g.begin(), g.end());
sort(s.begin(), s.end());
int child = 0, cookie = 0;
while (child < g.size() && cookie < s.size()) {
if (g[child] <= s[cookie])
++child;
++cookie;
}
return child;
}
};
135. 分发糖果
【题目描述】:一群孩子站成一排,每一个孩子有自己的评分。现在需要给这些孩子发糖果,规则是如果一个孩子的评分比自己身旁的一个孩子要高,那么这个孩子就必须得到比身旁孩子更多的糖果;所
有孩子至少要有一个糖果。求解最少需要多少个糖果。
【题解】:做完了题目455,你会不会认为在比较关系的贪心策略一定需要排序或是选择?虽然这一道题也是运用贪心策略,但我们只需要简单的两次遍历即可:把所有孩子的糖果数初始化为1;先从左往右遍历一遍,如果右边孩子的评分比左边高,则右边孩子的糖果更新为左边孩子的糖果数加1;再从右往左遍历一遍,如果左边孩子的评分比右边的高,且左边孩子当前的糖果数不大于右边孩子的糖果数,则左边孩子的糖果数更新为右边孩子的糖果数加1,通过两次遍历,分配的糖果就可以满足题目要求了。这里的贪心策略即为,再每次遍历中,只考虑并更新相邻一侧的大小关系。
class Solution {
public:
int candy(vector<int>& ratings) {
int size = ratings.size();
if (size < 2) return size;
vector<int>num(size, 1);
for (int i = 1; i < size; ++i) {
if (ratings[i] > ratings[i - 1])
num[i] = num[i - 1] + 1;
}
for (int i = size - 1; i > 0; --i) {
if (ratings[i] < ratings[i - 1])
num[i - 1] = max(num[i - 1], num[i] + 1);
}
return accumulate(num.begin(), num.end(), 0);
}
};
2.3 区间问题
435. 无重叠区间
【题目描述】:给定多个区间,计算让这些区间互不重叠所需要移除区间的最少个数。起止相连不算重叠。
【题解】:在选择要保留区间时,区间的结尾十分重要:选择的区间结尾越小,余留给其他区间的空间就越大,就能保留更多的区间。因此,我们采取的贪心策略为,优先保留结尾小且不相交的区间。
具体实现方法为,先把区间按照结尾的大小进行增序排序,每次选择结尾最小且和前一个选择的全局不重叠的区间。我们这里使用C++Lambda,结合std::sort()函数进行自定义排序。
在样例中,排序后的数组为{[1,2] ,[1,3],[2,4]}。按照我们的贪心策略,首先初始化为区间[1,2];由于[1,3]与[1,2]相交,我们跳过该区间;由于[2,4]与[1,2]不相交,我们将其保留。因此最终保留的区间为{[1,2],[2,4]}.
class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.empty()) return 0;
int n = intervals.size();
sort(intervals.begin(), intervals.end(),
[](const vector<int> &a, const vector<int>&b) {
return a[1] < b[1]; });
int total = 0, prev = intervals[0][1];
for (int i = 1; i < n; ++i)
if (intervals[i][0] < prev) ++total;
else prev = intervals[i][1];
return total;
}
};
55. 跳跃游戏
【题目描述】:给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标。
【题解】: 由于每层最多可以跳A[i]步,也可以跳0步或1步,因此如果能到达最高层,则说明每一层都可以到达。有了这个条件,说明可以用贪心算法。
思路一:正向,从0出发,一层一层往上跳,看到最后能不能超过最高层,能超过则说明能到达,否则不能到达。
思路二:逆向,从最高层下楼梯,一层一层下降,看最后能不能下降到第0层。
思路三:如果不敢用贪心,可以用动态规划,设状态为f[i],表示从第0层出发,走到A[i]时剩下的最大步数,则状态转移方程为:
f[i] = max(f[i-1],A[i-1])-1,i > 0
class Solution {
public:
bool canJump(vector<int>& nums) {
int reach = 1;
for (int i = 0; i < reach&&reach < nums.size(); ++i)
reach = max(reach, i + 1 + nums[i]);
return reach >= nums.size();
}
};
121. 买卖股票的最佳时机
【题目描述】:给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
【分析】:贪心算法,分别找到价格最低和最高的一天,低进高出,注意最低的一天要在最高的一天之前。把原始价格序列变成差分序列,本题也可以做是最大m子段和,m = 1。
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() < 2) return 0;
int profit = 0; //差价,也就是利润
int cur_min = prices[0]; //当前最小
for (int i = 1; i < prices.size(); i++) {
profit = max(profit, prices[i] - cur_min);
cur_min = min(cur_min, prices[i]);
}
return profit;
}
};
122. 买卖股票的最佳时机 II
【题目描述】:给定一个数组 prices ,其中 prices[i] 是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
【分析】:贪心算法,低进高出,把所有正的价格差价相加起来。把原始价格序列变成差分序列,本题可以做是最大m子段和, m = 数组长度。
class Solution {
public:
int maxProfit(vector<int>& prices) {
long long sum = 0;
for (int i = 1; i < prices.size(); i++) {
int diff = prices[i] - prices[i - 1];
if (diff > 0) sum += diff;
}
return sum;
}
};
3. 无重复字符的最长子串
【题目描述】:给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
【分析】:假设子串里含有重复字符,则父串一定含有重复字符,单个子问题就可以决定父问题,因此可以用贪心法,跟动态规划不同,动态规划里,单个子问题只能影响父问题,不足以决定父问题。
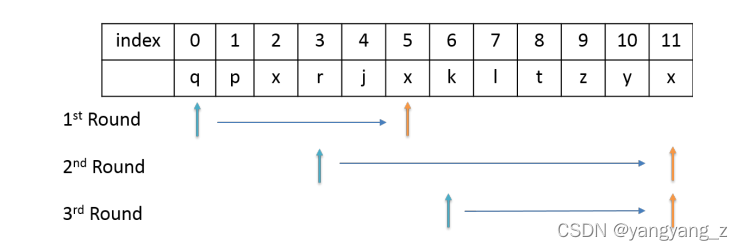
从左往右扫描,当遇到重复字母时,以上一个重复字母的index + 1,作为新的搜素起始位置,知道最后一个字母,复杂度O(n)
class Solution {
public:
int lengthOfLongestSubstring(string s) {
const int ASCCII_MAX = 255;
int last[ASCCII_MAX]; //记录字符上次出现过的位置
int start = 0; //记录当前子串中的起始位置
fill(last, last + ASCCII_MAX, -1); //0也是有效位置,因此初始化为-1
int max_len = 0;
for (int i = 0; i < s.size(); i++) {
if (last[s[i]] >= start) {
max_len = max(i - start, max_len);
start = last[s[i]] + 1;
}
last[s[i]] = i;
}
return max((int)s.size() - start, max_len);
}
};
11. 盛最多水的容器
【题目描述】:给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
【分析】:每个容器的面积,取决于最短的木板
class Solution {
public:
int maxArea(vector<int>& height) {
int start = 0;
int end = height.size() -1;
int result = INT_MIN;
while(start < end){
int area = min(height[end],height[start])*(end - start);
result = max(result,area);
if(height[start] <= height[end])
start++;
else end--;
}
return result;
}
};