QPSK调制及MATLAB实现
一、QPSK原理
QPSK规定了四种载波相位,分别为45°,135°,225°,315°,调制器输入的数据是二进制数字序列,为了能和四进制的载波相位配合起来,则需要把二进制数据变换为四进制数据,这就是说需要把二进制数字序列中每两个比特分成一组,共有四种组合,即00,01,10,11,其中每一组称为双比特码元。每一个双比特码元是由两位二进制信息比特组成,它们分别代表四进制四个符号中的一个符号。
双比特与载波相位的关系如表所示:
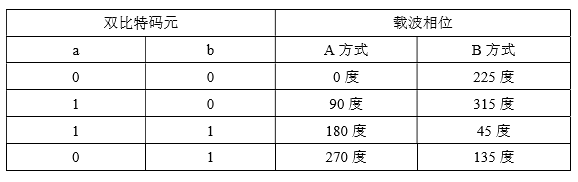
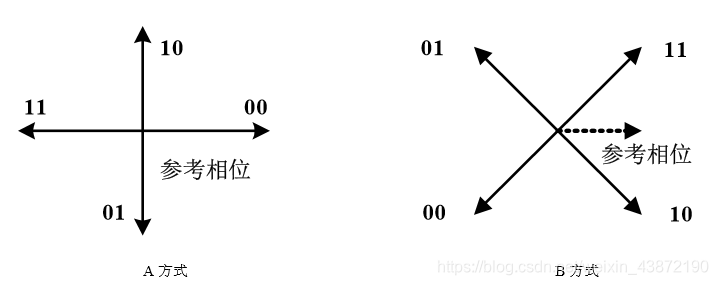


二、QPSK调制方法
QPSK信号产生的方法有两种,一种是相位选择法,如下图所示:
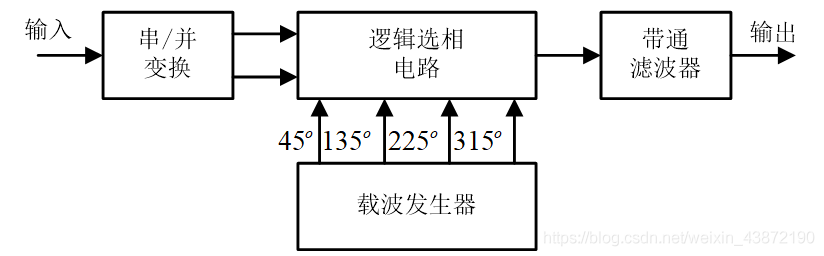
另一种是相乘电路,下面详细介绍:
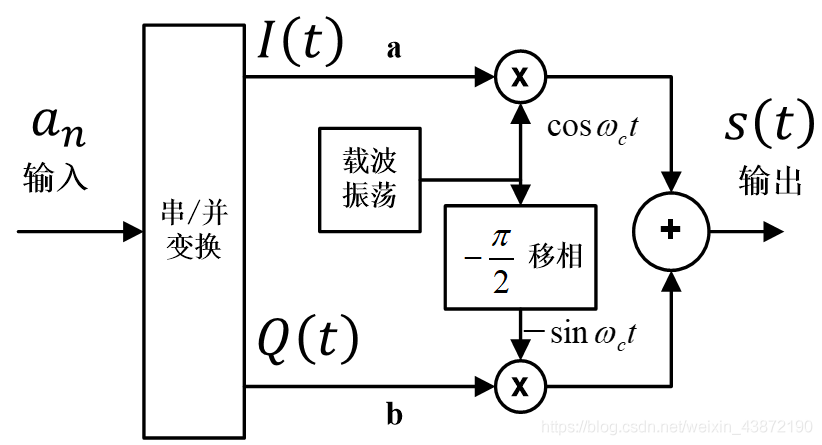
下图中输入的基带信号an是二进制不归零双极性码元,它被串并变换电路变成两路码元I(t)和Q(t)。[转换规则可以设定为奇数位为I(t),偶数位为Q(t)。例:1011001001 I(t):11010 Q(t):01001]变成并行码元I(t)和Q(t)后,其每个码元的持续时间是输入码元的2倍,这两路并行码元序列分别用以和两路正交载波相乘。在相加电路中相加后得到输出矢量s(t)。
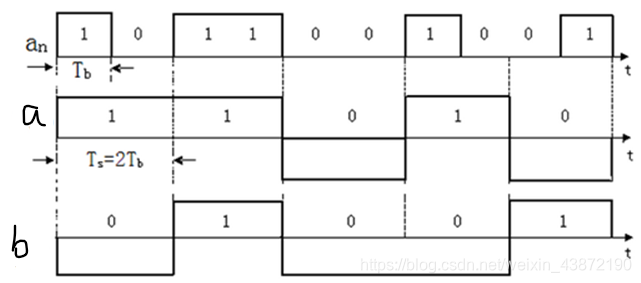
三、QPSK的时域波形
对于序列01 01 10 00 11 01 00,其按A、B方式调制的时域波形如下图所示:
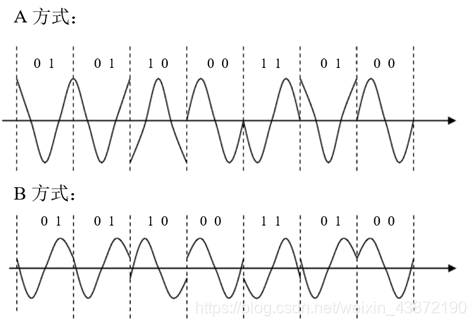
四、QPSK的功率谱
由于QPSK信号可被理解为由同相支路和正交支路两路2PSK叠加而成,但是载波的幅度与码元速率不同,因此QPSK信号的功率谱密度相当于2PSK信号的功率谱密度的线性叠加:
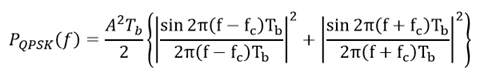
因此QPSK信号的功率谱示意图如下:
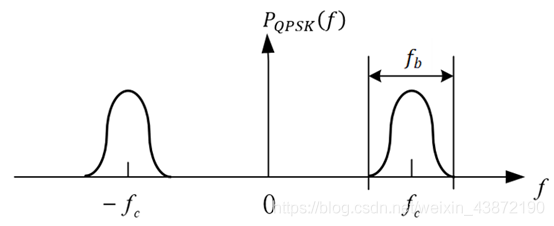
由上图可以看出其带宽等于基带码元速率,峰值频率为等于载波频率。
五、星座图的基本概念
在数字通信领域中,经常将数字信号在复平面上表示,以直观的表示信号以及信号之间的关系,这种图示就是星座图。星座图可以看成数字信号的一个“二维眼图”阵列,同时符号在图中所处的位置具有合理的限制或判决边界。如果要将数字信号发送出去,一般不会直接发0或1,而是先将0,1信号(bit)按照一个或者几个组成一组,比如每两个bit组成一组,即有00,01,10,11,总共四种状态,此时可以选择QPSK调制,QPSK四个点组成一个QPSK的星座图,每个点与相邻的点相差90度(幅度是相同的),一个星座点对应一个调制符号。星座图的作用主要是在调制时用于映射,而接收时用于判断发送的到底是哪个点,从而正确解调数据。
六、MATLAB实现QPSK已调信号生成的思路
按照QPSK调制原理,将信源进行串/并转换,分别即取出信源(m序列)的奇偶位,并将码速变为原来的一半,接着将该单极性非归零信号变为双极性非归零信号。对该两路信号进行采样,对奇数列采样序列乘cos(2πf_c t)减去偶数列采样序列乘sin(2πf_c t),得到QPSK信号。对QPSK信号进行fft再进行fftshift求其频谱。将基带信号两位两位组合,映射到QPSK星座图,画图得到信源星座图。