【华为机试在线训练】Day 7

题目描述

请实现如下接口

    /* 功能：四则运算

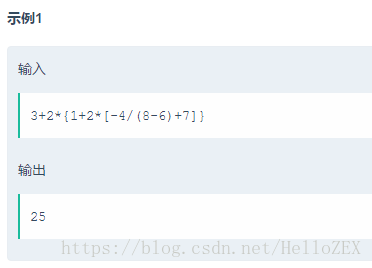
     * 输入：strExpression：字符串格式的算术表达式，如: "3+2*{1+2*[-4/(8-6)+7]}"

         * 返回：算术表达式的计算结果

     */

    public static int calculate(String strExpression)

    {

        /* 请实现*/

        return 0;

    } 

约束：

1. pucExpression字符串中的有效字符包括[‘0’-‘9’],‘+’,‘-’, ‘*’,‘/’ ,‘(’， ‘)’,‘[’, ‘]’,‘{’ ,‘}’。

2. pucExpression算术表达式的有效性由调用者保证; 

输入描述:

输入一个算术表达式

输出描述:

得到计算结果

//先中缀转后缀再计算后缀表达式的值，需要注意的是对于‘-’为一元运算符的处理和数字//的位数做一个记录。当看到python只有一行代码时，吐了一口老血。。。
#include<iostream>
#include<string>
#include<vector>
#include<stack>
using namespace std;
int main() {
    string s;
    while (cin >> s) {
        stack<char> opera;
        vector<int> numcnt;//用来保存每个数字的位数，以保证计算后缀表达式时的正确性
        string s1;//后缀表达式
        //中缀表达式转后缀表达式
        for (int i = 0;i<s.size();i++) {
            if (s[i] >= '0'&&s[i] <= '9') {
                int tmp = 0;
                while (s[i] >= '0'&&s[i] <= '9') {
                    tmp++;
                    s1 += s[i];
                    i++;
                }
                i--;
                numcnt.push_back(tmp);
            }
            else if (s[i] == '-' || s[i] == '+') {
                if (s[i] == '-' && (s[i - 1] == '(' || s[i - 1] == '[' || s[i - 1] == '{'))
                    s1 += '0';
                while (!opera.empty()&&(opera.top() == '*' || opera.top() == '/' || opera.top() == '+' || opera.top() == '-')) {
                    s1 += opera.top();
                    opera.pop();
                }
                opera.push(s[i]);
            }
            else if (s[i] == '*' || s[i] == '/') {
                while (!opera.empty()&&(opera.top() == '*' || opera.top() == '/')) {
                    s1 += opera.top();
                    opera.pop();
                }
                opera.push(s[i]);
            }
            else if (s[i] == '(' || s[i] == '[' || s[i] == '{')
                opera.push(s[i]);
            else if (s[i] == ')') {
                while (opera.top() != '(') {
                    s1 += opera.top();
                    opera.pop();
                }
                opera.pop();
            }
            else if (s[i] == ']') {
                while (opera.top() != '[') {
                    s1 += opera.top();
                    opera.pop();
                }
                opera.pop();
            }
            else if (s[i] == '}') {
                while (opera.top() != '{') {
                    s1 += opera.top();
                    opera.pop();
                }
                opera.pop();
            }
            else
                cout << "Invalid input!" << endl;
        }
        while (!opera.empty()) {
            s1 += opera.top();
            opera.pop();
        }
        //计算后缀表达式的值
        stack<int> nums;
        int ind = 0;
        for (int i = 0;i<s1.size();i++) {
            if (s1[i] >= '0'&&s1[i] <= '9') {
                int total = 0;
                while (numcnt[ind]--)
                    total = 10 * total + (s1[i++] - '0');
                i--;
                nums.push(total);
                ind++;
            }          
            else {
                int tmp1 = nums.top();
                nums.pop();
                int tmp2 = nums.top();
                nums.pop();
                if (s1[i] == '+')
                    nums.push(tmp2 + tmp1);
                else if (s1[i] == '-')
                    nums.push(tmp2 - tmp1);
                else if (s1[i] == '*')
                    nums.push(tmp2*tmp1);
                else
                    nums.push(tmp2 / tmp1);
            }
        }
        cout << nums.top() << endl;    
    }
}

---

---

参考：https://blog.csdn.net/shizheng163/article/details/50988023

题目描述

Levenshtein 距离，又称编辑距离，指的是两个字符串之间，由一个转换成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。编辑距离的算法是首先由俄国科学家Levenshtein提出的，故又叫Levenshtein Distance。

Ex：

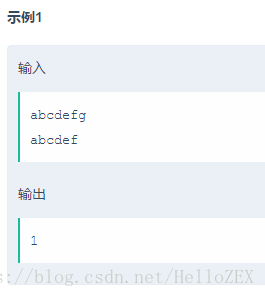
字符串A:abcdefg

字符串B: abcdef

通过增加或是删掉字符”g”的方式达到目的。这两种方案都需要一次操作。把这个操作所需要的次数定义为两个字符串的距离。

要求：

给定任意两个字符串，写出一个算法计算它们的编辑距离。

 

请实现如下接口

/*  功能：计算两个字符串的距离

 *  输入： 字符串A和字符串B

 *  输出：无

 *  返回：如果成功计算出字符串的距离，否则返回-1

 */

     public   static   int  calStringDistance (String charA, String  charB)

    {

        return  0;

    }  

 

输入描述:

输入两个字符串

输出描述:

得到计算结果

//典型的动态规划优化编辑器问题
//参考博客 http://blog.csdn.net/shizheng163/article/details/50988023
#include<iostream>
#include <string>
#include <vector>
using namespace std;
int calStringDistance(string a,string b){
    int n = (int)a.size(),m = (int)b.size();
    vector<vector<int>>dp(n+1,vector<int>(m+1,0));
    dp[0][0] = 0;//dp[x][y]代表将a字符串前x个字符修改成b字符串前y个字符
    for (int i=1; i<=m; ++i) dp[0][i] = i;
    for (int i=1; i<=n; ++i) dp[i][0] = i;
    for (int i=1; i<=n; ++i) {
        for (int j=1; j<=m; ++j) {
            int one = dp[i-1][j] +1,two = dp[i][j-1]+1,three = dp[i-1][j-1];
            if(a[i-1]!=b[j-1]) three+=1;
            dp[i][j] = min(min(one,two),three);
        }
    }
    return dp[n][m];
}
int main(){
    string a,b;
    while(cin>>a>>b)
        cout<<calStringDistance(a, b)<<endl;
    return 0;
}

---

---

题目描述

题目描述

把M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？（用K表示）5，1，1和1，5，1 是同一种分法。

 

输入

每个用例包含二个整数M和N。0<=m<=10，1<=n<=10。

 

样例输入

7 3

 

样例输出

8

 

/**

* 计算放苹果方法数目

* 输入值非法时返回-1

* 1 <= m,n <= 10

* @param m 苹果数目

* @param n 盘子数目数

* @return 放置方法总数

*

*/

public static int count(int m, int n)

输入描述:

输入两个int整数

输出描述:

输出结果，int型

#include<iostream>
#include<cstdlib>
using namespace std;
int count1(int m,int n)
{
    if(m==0 || n==1)
    {
    return 1;
    }
    if(m<n)
    {
        return count1(m,m);
    }
    else
    {
        return (count1(m,n-1)+count1(m-n,n));
    }
}
int main()
{
    int m;
    int n;
    while(cin>>m>>n)
    {
        cout<<count1(m,n)<<endl;
    }
    return 0;
}
/*  解题分析：
        设f(m,n) 为m个苹果，n个盘子的放法数目，则先对n作讨论，
        当n>m：必定有n-m个盘子永远空着，去掉它们对摆放苹果方法数目不产生影响。即if(n>m) f(m,n) = f(m,m)　　
        当n<=m：不同的放法可以分成两类：
        1、有至少一个盘子空着，即相当于f(m,n) = f(m,n-1); 
        2、所有盘子都有苹果，相当于可以从每个盘子中拿掉一个苹果，不影响不同放法的数目，即f(m,n) = f(m-n,n).
        而总的放苹果的放法数目等于两者的和，即 f(m,n) =f(m,n-1)+f(m-n,n)
    递归出口条件说明：
        当n=1时，所有苹果都必须放在一个盘子里，所以返回１；
        当没有苹果可放时，定义为１种放法；
        递归的两条路，第一条n会逐渐减少，终会到达出口n==1;
        第二条m会逐渐减少，因为n>m时，我们会return f(m,m)　所以终会到达出口m==0．
*/

---

---