离散数学实验-C++实现集合关系判定
离散数学实验-C++实现集合有关关系的判断
1. 程序的设计思路与实现功能
1.求传递闭包:对于任意顶点i和j,若两顶点连通但非邻接点,且包含前n个点作为路径的中间节点,则添加将对应的m[i][j]赋为1。
2.等价:若满足自反,对称,传递性,则为等价关系。
3.等价类:对于有关系的点,输出与它有关系的点:若m[i][j]==1,输出每一个j元素。
4.划分:输出等价类,若已输出相同的等价类,则不输出该元素的等价类。
功能是:
对于给定的整数集合与对应关系
1.求关系的性质(自反,对称,传递,等价)
2.求关系的单个或多个闭包(自反,对称,传递,等价)
3.对于等价关系,输出划分
4.对于等价关系,输出等价类
注:好像用的不是warshall算法,不太懂,虽然做出了。
实验环境:C++,Code::Blocks
2. 编程调试过程中遇到的问题及其解决过程
1.划分时相同等价类的重复输出,重新调整了程序的运行顺序。
2.输出了多余的{},重新调整了程序的运行顺序。
3.一些马虎的问题,检查并解决。
3.程序代码与运行结果
#include<iostream>
#include<stdlib.h>
#include<string.h>
#include<fstream>
#define MAXE 16
using namespace std;
bool is_eql,m_saved,m_added;//标记
int x=0;//结束符
class Relation
{
public:
Relation();
void clrmem();
int Getpnum(){return pnum;}
int Checkp(int p);
int Read();
void Write();//读写
void EnterMtx();
void Enter();
int CtrlZ();//撤销闭包运算
void ShowSet();
void ShowMtx();
bool Judge();//判断关系
void GetClosure(bool gain[]);//计算闭包
void Closure();//闭包菜单
void EqualClass();//显示等价类
void ShowPart();//显示划分
private:
int sets[MAXE];
bool matrix[MAXE][MAXE];//使用的矩阵
bool msave[MAXE][MAXE];//备份的矩阵
bool madd[MAXE][MAXE];//闭包运算中添加的关系,以矩阵方式储存
int pnum;
int rnum;//点和关系的数量
int radd;
}rs1;
int ckerror()
{//查错
if(cin.fail())
{
cin.clear();
cin.sync();
return 1;//有误
}
return 0;//无误
}
Relation::Relation()
{初始化
memset(sets,0,MAXE*sizeof(int));
memset(matrix,false,(MAXE*MAXE)*sizeof(bool));
memset(msave,false,(MAXE*MAXE)*sizeof(bool));
memset(madd,false,(MAXE*MAXE)*sizeof(bool));
pnum=0,rnum=0;
}
void Relation::clrmem()
{//清空关系
memset(sets,0,MAXE*sizeof(int));
memset(matrix,false,(MAXE*MAXE)*sizeof(bool));
pnum=0,rnum=0;
}
int Relation::Checkp(int p)
{//检查元素存在
for(int i=0;i<pnum;i++)
if(sets[i]==p) return i;
return -1;//没有找到对应的元素
}
int Relation::Read()
{//读入
ifstream fin("mtx.txt");
if(!fin.is_open()) return 1;//无记录数据/未成功打开
clrmem();
fin>>x>>pnum;
for(int i=0;i<pnum;i++)
fin>>sets[i];
rnum=pnum*pnum;
for(int i=0;i<pnum;i++)
for(int j=0;j<pnum;j++)
fin>>matrix[i][j];
fin.close();
return 0;//成功读入
}
void Relation::Write()
{//保存
fstream fout;
fout.open("mtx.txt",ios::out);
fout<<x<<'\r'<<pnum<<'\r';
for(int i=0;i<pnum;i++)
fout<<sets[i]<<' ';
fout<<'\r';
for(int i=0;i<pnum;i++)
{
for(int j=0;j<pnum;j++)
fout<<matrix[i][j]<<' ';
fout<<'\r';
}
fout<<"//存储的数据依次为:结束标识符,集合元素数,集合,关系矩阵";
fout.close();
}
void Relation::EnterMtx()
{//修改关系矩阵
int xx,yy;
cout<<"请输入关系,以“"<<x<<' '<<x<<"”结束"<<endl;
cout<<"例如“1 4 2 3 "<<x<<' '<<x<<"”代表M={<1,4>,<2,3>}"<<endl;
while(1)
{
cin>>xx>>yy;
if(ckerror()){cout<<"输入有误";exit(0);}
if(xx==x&&yy==x) break;
xx=Checkp(xx);
yy=Checkp(yy);
if(xx==-1||yy==-1) continue;//如果输入不存在的元素,忽视这次输入 --checkp返回-1,则不存在
matrix[xx][yy]=1;
}
Write();
}
void Relation::Enter()
{//输入
/*输入集合部分*/
clrmem();
cout<<"请输入集合中的元素,以空格隔开,以"<<x<<"结束:";
for(int i=0;i<MAXE;i++)
{
cin>>sets[i];
if(ckerror()) {cout<<"输入有误";exit(0);}
for(int j=0;j<i;j++)
if(sets[j]==sets[i])
{
sets[i--]=0;
break;
}
if(sets[i]==x){pnum=i;break;}
}
rnum=pnum*pnum;
ShowSet();
/*输入矩阵部分*/
EnterMtx();
Write();//输入后保存
}
int Relation::CtrlZ()
{
memcpy(matrix,msave,(MAXE*MAXE)*sizeof(bool));
memset(msave,false,(MAXE*MAXE)*sizeof(bool));
m_saved=false;
Write();
return 1;
}
void Relation::ShowSet()
{//显示集合
cout<<"集为";
if(pnum==0) {cout<<"空集 |"<<endl;return;}
cout<<'{';
for(int i=0;i<pnum;i++)
{
cout<<sets[i];
if(i!=pnum-1) cout<<',';
}
cout<<'}'<<endl;
}
void Relation::ShowMtx()
{//显示矩阵
if(pnum==0) {cout<<"集合中无元素 |"<<endl;return;}//不存在 返回
cout<<"矩阵M="<<endl;
for(int i=0;i<pnum;i++)
{
for(int j=0;j<pnum;j++)
cout<<matrix[i][j]<<' ';
cout<<endl;
}
}
bool Relation::Judge()
{//性质判断
bool F_reflex=true,F_ireflex=true,F_symme=true,F_isymme=true,F_trans=true;
if(pnum==0) return false;
for(int i=0;i<pnum;i++)
if(!matrix[i][i]) //若对角线上有0
F_reflex=false;
if(F_reflex) cout<<"具有自反性 |"<<endl;
for(int i=0;i<pnum;i++)
if(matrix[i][i]) //对角线上有1
F_ireflex=false;
if(F_ireflex) cout<<"具有反自反性 |"<<endl;
for(int i=0;i<pnum;i++)
for(int j=0;j<pnum;j++)
if((matrix[i][j] && !matrix[j][i]))//若存在<i,j>,不存在<j,i>
F_symme=false;
if(F_symme) cout<<"具有对称性 |"<<endl;
for(int i=0;i<pnum;i++)
for(int j=0;j<pnum;j++)
if(matrix[i][j] && matrix[j][i] && i != j) //若存在<i,j>与<j,i>,且i不是j
F_isymme=false;
if(F_isymme) cout<<"具有反对称性 |"<<endl;
for(int i=0;i<pnum;i++)
for(int j=0;j<pnum;j++)//遍历矩阵,对于集合中任意两点i,k
if(matrix[i][j]==1)//若存在中途点j即存在<i,j>
for(int k=0;k<pnum;k++)
if(matrix[j][k]&&!matrix[i][k]) //与<j,k>,若无<i,k>,则无传递性
F_trans=false;
if(F_trans) cout<<"具有传递性 |"<<endl;
is_eql=(F_reflex&&F_symme&&F_trans);
if(is_eql) cout<<"是等价关系 |"<<endl;
return true;
}
void Relation::GetClosure(bool gain[4])
{//计算闭包
/*存储矩阵,清空相关数据*/
radd=0;
m_added=false;
m_saved=false;
memcpy(msave,matrix,(MAXE*MAXE)*sizeof(bool));
memset(madd,false,(MAXE*MAXE)*sizeof(bool));
m_saved=true;
/*计算部分*/
bool t;//传递闭包中间变量
if(gain[0]){//自反闭包
for(int i=0;i<pnum;i++)
if(matrix[i][i]==0)
{madd[i][i]=matrix[i][i]=1;radd++;}
}
if(gain[1]){//对称闭包
for(int i=0;i<pnum;i++)
for(int j=0;j<pnum;j++)
if(matrix[i][j]==1&&matrix[j][i]==0)
{madd[j][i]=matrix[j][i]=1;radd++;}
}
if(gain[2]){//传递闭包
for(int n=0;n<pnum;n++)
for(int i=0;i<pnum;i++)
for(int j=0;j<pnum;j++)
{
t=matrix[i][n]*matrix[n][j];
if(t&&!matrix[i][j]) madd[i][j]=matrix[i][j]=t;//若改变
}
}
}
void Relation::Closure()
{//闭包运算菜单
/*交互部分*/
int n;
char asks[5];
bool gain[4]={false};
cout<<"1.自反闭包 2.对称闭包 3.传递闭包 4.等价闭包"<<endl;
cout<<"请输入您需要做的闭包运算的序号(同时输入多个,例如 12 即求自反与对称闭包)"<<endl;
cin>>asks;
ckerror();
for(int i=0;asks[i]!='\0'&&i<5;i++)
if(asks[i]<'1'||asks[i]>'4')
{//除错
cout<<"您的输入有误,已返回"<<endl;
return;
}
//此时得到了只含有选项对应数字字符的数组
for(int i=0;asks[i]!='\0'&&i<5;i++)
{
n=asks[i]-49;//数字为-48,再-1为下标
gain[n]=true;
}
if(gain[3]) memset(gain,true,3*sizeof(bool));
GetClosure(gain);
if(radd) m_added=true;
Write();
if(!m_added) return;
cout<<"做M∪M`运算,M`={";
for(int i=0;i<pnum;i++)
for(int j=0;j<pnum;j++)
if(madd[i][j]==1) cout<<'<'<<sets[i]<<','<<sets[j]<<">,";
cout<<'}'<<endl;
system("pause");
}
void Relation::EqualClass()
{
for(int i=0;i<pnum;i++)
{
cout<<'['<<sets[i]<<"]R={";
for(int j=0;j<pnum;j++)
if(matrix[i][j])cout<<sets[j]<<',';
cout<<"}"<<endl;
}
system("pause");
}
void Relation::ShowPart()
{
int temp[MAXE]={0};
cout<<"该集合的划分为{";
for(int i=0;i<pnum;i++)
{
if(temp[i]==0)
{
cout<<'{';
for(int j=0;j<pnum;j++)
if(matrix[i][j]&&temp[j]==0) {cout<<sets[j]<<',';temp[j]=1;}
cout<<"\b}";
}
}
cout<<'}'<<endl;
}
void NoData()
{//初始化
if(rs1.Read())
{
cout<<"请输入结束输入的标识符:";
cin>>x;
ckerror();
rs1.Enter();//若没有记录,则进行记录
rs1.Write();
}
}
int Functions()
{//显示主体
int choice;
while(1)
{
system("cls");
rs1.Read();
cout<<"结束符为:"<<x<<endl;
cout<<"-----------------@"<<endl;
rs1.ShowSet();
rs1.ShowMtx();
if(!rs1.Getpnum()) cout<<"-----------------@"<<endl;
if(rs1.Getpnum()) cout<<"-------------@"<<endl;
rs1.Judge();//这里是运算部分
if(rs1.Getpnum()) cout<<"-------------@"<<endl;
if(is_eql) rs1.ShowPart();
cout<<"\n请选择:"<<endl;
cout<<"1.重新输入数据"<<endl;
cout<<"2.重新输入结束符"<<endl;
cout<<"3.添加关系"<<endl;
cout<<"4.进行闭包运算"<<endl;
if(m_saved)cout<<"5.撤销最近一次闭包运算"<<endl;
if(is_eql) cout<<"6.显示等价类"<<endl;
cout<<"0.保存并退出"<<endl;
cin>>choice;
ckerror();
switch(choice)
{
case 1:
rs1.Enter();
m_saved=0;
break;
case 2:
cin>>x;
ckerror();
rs1.Write();
break;
case 3:
rs1.EnterMtx();
break;
case 4:
rs1.Closure();
break;
case 5:
if(m_saved)
if(rs1.CtrlZ())
cout<<"恢复成功"<<endl;
break;
case 6:
if(is_eql) rs1.EqualClass();
break;
case 0:
rs1.Write();
return 0;
break;
default:
break;
}
}
}
int main()
{
NoData();
Functions();
return 0;
}
程序的运行结果:
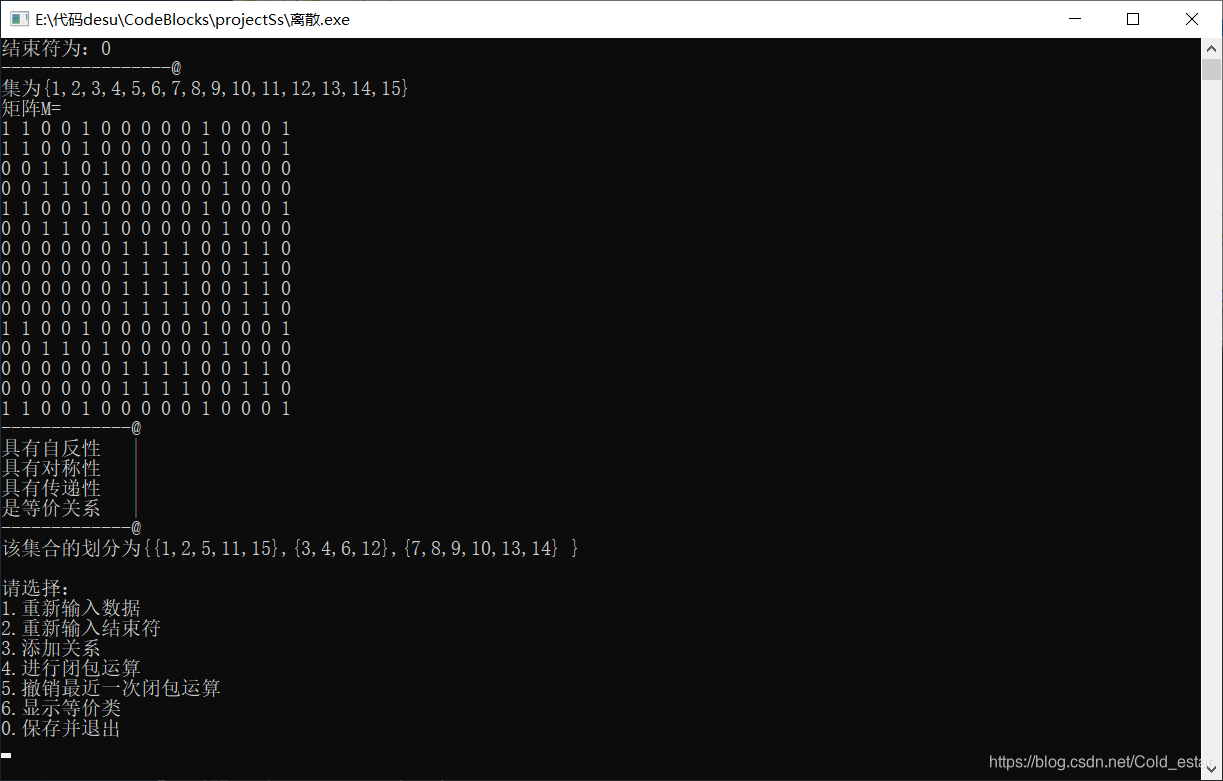
4总结(心得体会)
编程得到结果的时候是很快乐的,我发觉计算机的优势是能够按照确定的程序进行快速的大量重复计算,
我对离散数学的知识也有了进一步的理解。
5.参考资料
Warshell算法学习与实现:https://www.cnblogs.com/lpshou/archive/2012/04/27/2473109.html
360百科 Warshell算法: https://baike.so.com/doc/5312044-5547048.html