一文彻底读懂【极大似然估计】
极大似然估计(Maximum Likelihood Estimate)
一、背景知识
- 1822年首先由德国数学家高斯(C. F. Gauss)在处理正态分布时首次提出;
- 1921年,英国统计学家罗纳德·费希尔(R. A. Fisher)证明其相关性质,得到广泛应用,数学史将其归功于费希尔。
- 研究问题本质背后的深刻原因在于,现实世界本身就是不确定的,人类的观察能力是有局限性的,就是利用已知的样本信息,反向推导最有可能(即最大概率)导致这些样本结果出现的模型参数值。
- 极大似然估计,提供了一种给定观察数据来评估模型参数的方法。也就是似然函数的直观意义是刻画参数 与样本数据的匹配程度。
二、从概率模型理解极大似然估计
- 离散型统计模型:
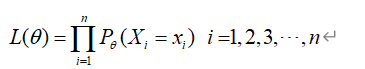
- 连续型统计模型:
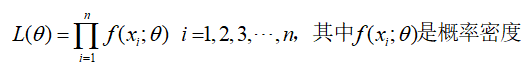
- 从一个直观的例子理解极大似然估计,比如:在一个未知的袋子里摸球,现有的认知告诉我们是袋子里面的球要么是红色,要么是蓝色。于是我们可以知道从该袋子中摸球颜色的概率服从二项分布如下:
| X | 红色 | 蓝色 |
|---|---|---|
| P | θ | 1-θ |
- 由于不知道袋子中究竟有多少个球以及每个颜色的球有多少个,所以无法对参数θ进行计算,也不能计算出摸到哪种颜色的球的概率是多少?于是,假设有一个测试人员对袋内球进行有放回的抽取,进行了100次随机测验之后,统计得出:有30次摸到的是红球,有70次摸到的是蓝球。
- 从现有的测试结果出发,我们有理由相信袋子中球的比例大概是红色 : 蓝色=3 : 7(也就是背后的理论支撑)。所以进而求出概率以及参数 θ=0.3 。也就是用抽样时球的颜色出现的频率近似等于概率。
注意的是,极大似然估计中采样需满足一个重要的假设,就是所有的采样都是独立同分布的。

如何理解这个公式呢?由于抽样的结果是确定的,而每次抽样的积事件组成了现在已知的既定事件,所以“独立同分布”且属于二项分布。而现在我们的求解目的转为:使似然函数最大化,因为事件已经确定发生了,我们根据观测的结果出发,则使其“积事件”的概率无限接近于1(因为已经发生了嘛)也就是说最大化。
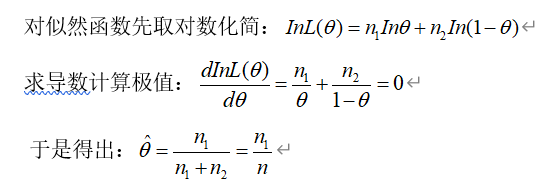
这样就从理论化的角度描述了“状态1”发生的概率与直观一致,为了使总体参数尽可能与现有观测值相匹配,所以要让似然函数达到最大值。
三、极大似然估计的理论原理
上面的描述为了直观和简洁,忽视了逻辑上和表示上的严谨性。下面从纯理论化的语言进行严格描述。不过在使用极大似然估计时,始终要记住的是:独立同分布。
涉及太多公式,造成阅读不便还请谅解!


注意这里的 是一个向量,因为往往求解的模型参数不止一个。然后根据所求的偏导数利用梯度下降法逐步更新参数,以取得近似最优解。
为了便于理解计算的过程,这里通过正态分布的样本随机变量进行模拟求解,正态分布的公式如下:
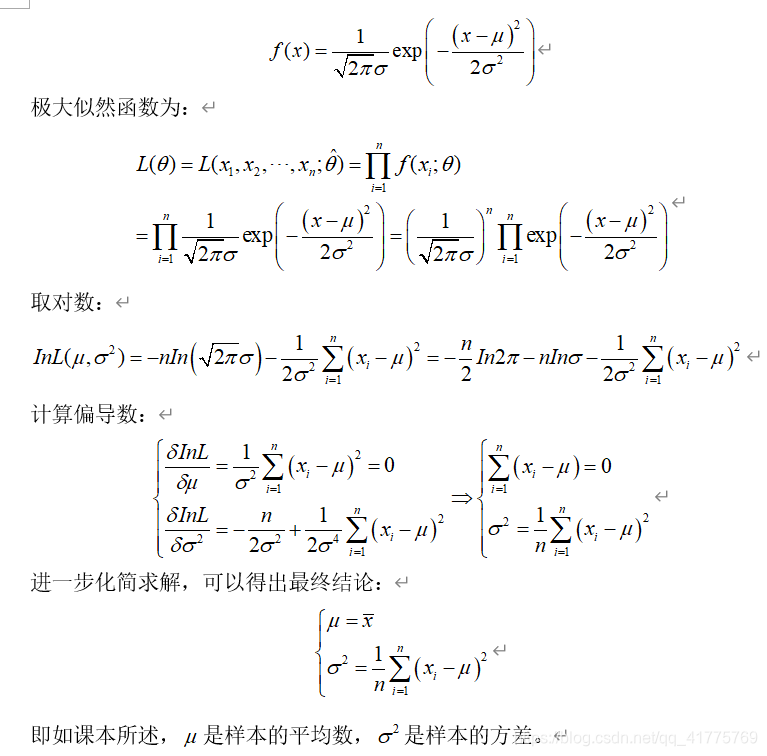
四、应用场景
极大似然估计在机器学习的理论算法研究中应用广泛,尤其是涉及到机器学习损失函数最小化时,往往会在似然函数中添加负号,以达到最小化的目的。先研究线性回归时,不仅可以根据MSE建立最小误差函数,也可以从正态分布和极大似然估计的角度进行推导。机器学习算法中使用极大似然估计的算法有朴素贝叶斯、EM算法等。
另外极大似然函数特别擅长于处理与概率相关的问题,因为模型的求解往往就是参数的求解,根据批量的随机样本最大化近似或者模拟现实世界,在应用中使用得比较频繁的往往还是离散型随机变量的似然函数求解,而连续型以正态分布函数较为常见。利用极大似然估计建立的损失函数模型,需要进一步借助梯度下降法来不断的更新迭代参数,来对参数进行求解。