使用 LJ1-01 夜间灯光图像检测县域经济发展:与 NPP-VIIRS 数据的比较
抽象的
夜间灯光(NTL)遥感数据已被广泛用于推导国家和区域尺度的社会经济指标,以研究区域经济发展。然而,以往的研究大多只选择单一的衡量指标(如GDP),采用简单的回归方法,基于DMSP-OLS或NPP-VIIRS稳定的NTL数据来考察某一地区的经济发展情况。现状表明,单一评价指标存在问题——评价精度低。LJ1-01卫星是全球首颗NTL专用遥感卫星,于2018年7月发射,LJ1-01提供的数据具有更高的空间分辨率和较少的晕染现象。本文比较了LJ1-01数据和NPP-VIIRS数据在检测县域多维经济发展中的准确性。在中国湖北、湖南和江西三省,从经济条件、民生、社会发展、公共资源和自然脆弱性五个方面选取了20个社会经济参数。然后,构建县级经济指数(CEI)来评估多维经济发展水平,并确定研究区域内多维经济发展的空间格局。本研究采用随机森林(RF)和线性回归(LR)算法分别建立回归模型,并通过交叉验证对结果进行评估。结果表明,RF算法与LR算法相比,大大提高了模型的精度,适用于NTL数据的研究。此外,2 ) 基于 LJ1-01 数据 (0.8168) 在 RF 模型中比从 NPP-VIIRS 数据 (0.7245) 获得,这反映 LJ1-01 数据在社会经济参数评估中具有更好的潜力,可以用于准确有效地识别县级多维经济发展。
关键词: LJ1-01;NPP-VIIRS ; 县级经济指标;随机森林 (RF) 回归
一、介绍
由于人类活动、交通建设和城市扩张的迅速增加导致城市灯光强度的增加,人造灯的可用性通常与财富和现代社会联系在一起 [ 1 , 2 ]。以往的研究 [ 3 , 4 , 5 ] 表明,与普通光学遥感图像相比,夜间光(NTL)数据更能反映人类活动与社会发展的关系,被广泛应用于社会经济参数预测、动态监测。城市化进程、能源消耗估算和环境评估等。
目前,两种广泛使用的NTL产品是国防气象卫星计划——运营线扫描系统(DMSP-OLS)稳定NTL数据和Suomi国家极轨合作伙伴——可见红外成像辐射计套件(NPP-VIIRS)NTL数据[ 6 ]。DMSP-OLS稳定的年夜光数据产品由6个不同的卫星传感器获得,包括1992年至2013年的34幅年度图像,但存在辐射校准不足、空间分辨率低、信号过饱和等问题[ 7]]。作为 DMSP-OLS 传感器的继任者,NPP-VIIRS 自 2012 年以来提供了一系列白天/夜间波段夜间灯光的高质量图像,并对 DMSP-OLS 数据进行了重大改进,包括更宽的测量范围、更高空间分辨率和机载校准 [ 8 , 9 ]。以往的研究表明,与DMSP-OLS数据相比,NPP-VIIRS图像在城市建成区测绘和社会经济参数估计方面具有更高的精度[ 10 , 11 ]。中国武汉大学研制的新一代NTL卫星LJ1-01于2018年6月2日成功发射[ 12]]。LJ1-01是世界上第一颗夜光遥感专用卫星,也是第一颗具有对地观测能力和增强型卫星导航的低轨卫星[ 13 ]。与 DMSP-OLS 和 NPP-VIIRS 相比,LJ1-01 以更精细的空间分辨率(~130 m)获取 NTL 数据,具有 14 位量化和 15 天的重访时间。LJ1-01 数据的更高空间分辨率意味着可以显示更多的光源空间细节 [ 14 ]。此外,LJ1-01 数据不会遇到与 DMSP-OLS 数据相同的饱和度和泛光问题,因为传感器能力、光源的差距在 LJ1-01 图像中的周围区域的平均化程度较低,其具有更高的空间分辨率 [ 15]。这三种NTL数据的规格如表1所示。这些优势可以极大地提高检测人工照明的能力,为人类活动、城市建设和社会发展的研究提供新的见解和可能性。多项研究表明,与 NPP-VIIRS NTL 数据相比,LJ1-01 影像数据可以提供更多容量。江等人。[ 12 ]证实LJ1-01数据在用于调查城市光污染时比NPP-VIIRS数据更有效。李等人。[ 13 ] 还发现LJ1-01数据可以取得更好的城市区域图提取结果。张等人。[ 16] 应用 LJ1-01 和 NPP-VIIRS NTL 数据来估计 10 个社会经济参数,并得出结论认为前者可以作为衡量社会经济指标的更有效工具。然而,他们只关注地级层面的单一维度指标的评价,并没有对县级经济数据进行更全面的分析。因此,本研究探索LJ1-01 NTL数据在县级综合经济指标评价中的潜力,以更好地验证LJ1-01 NTL数据在城市发展分析和社会经济研究中的意义和价值。
表 1. 三种夜间灯光 (NTL) 数据的规格。


目前,基于 NTL 数据的社会经济参数估计研究大多是在国家、省或地级空间单位进行的,而分析县级区域经济发展的研究相对较少。由于县是中国行政区划的基本单位,县域经济是国民经济的基本单位,在国民经济发展中占有极其重要的地位。近年来,县域经济发展迅速。于是,县域发展不平衡的问题逐渐浮出水面,最终成为学者们关注的热点 [ 17 , 18 , 19 , 20 ]]。以往关于区域经济差异的研究大多选择单一的衡量指标,如人均GDP或GDP,采用标准差、变异系数、线性回归等传统方法来考察某一区域的经济发展状况。21 , 22 ]。这些研究表明,社会经济活动与大范围(例如,在国家或省级层面)的夜间光照强度密切相关,这可以通过回归模型很好地描述。但近年来,经济评价指标的选择发生了变化,逐渐从单一指标向更能反映一个县域综合经济状况的多维指标过渡[ 23]。]。结合因子分析、层次分析法、主成分分析等综合评价县域经济发展状况,结合基于GIS的探索性空间数据分析(ESDA)技术,帮助人们揭示区域经济发展状况以及从空间角度看失衡的演变。这使得经济模型和自然条件之间的差异更加显着,经济参数与 NTL 之间的关系在更精细的尺度上(例如,在县或镇级别)更加复杂。作为单一的全局模型,经典线性回归可能无法正确捕捉复杂的关系 [ 24]。近年来,机器学习方法由于其高预测精度而更常用于遥感应用中的分类或回归 [ 25 , 26 , 27 ]。在各种机器学习方法中,随机森林(RF)因其能够处理复杂关系、识别因变量和自变量之间的关系、对噪声的敏感性低以及能够避免过度拟合等优点而日益突出[ 28,29 , 30 ]。RF 回归模型最近已成功与 NTL 和其他多源数据相结合,用于人口网格划分和人类活动检测 [ 31,32 ]。然而,很少有研究应用于 LJ1-01 数据。因此,本研究旨在探索 RF 算法在 LJ1-01 和 NPP-VIIRS 数据中的应用,以检测县级经济发展。本文还比较了传统的线性回归(LR)。
我们的主要贡献总结如下:(1)基于熵校正层次分析法(Entropy-AHP)和社会经济统计数据,得出湖北、湖南、江西各县县级经济指数(CEI)各省的计算综合反映了该地区的经济发展情况。(2) 选择夜间灯光影像的几个特征作为多维指标;然后,使用随机森林算法(RF)建立数学模型,并将结果与传统线性回归算法(LR)的结果进行比较。分别使用两种NTL(LJ1-01/NPP-VIIRS)数据对CEI进行回归,以识别县域经济的发展情况。还给出了这两个结果集的比较分析。(3)运用一系列基于GIS的地统计学方法对研究区县域经济空间格局进行分析,得出一些可靠且有价值的结论。本文的其余部分安排如下:第2节介绍了本文的材料和方法,然后是第3节和第4节,对结果进行了分析和讨论。最后,第 5 节总结了本研究的结果,并提供了进一步研究的前景。
2。材料和方法
2.1. 学习区
如图1所示选取湖北、湖南、江西三省作为研究区进行比较。研究区位于中华人民共和国中部,东经108°21′~东经118°29′,北纬24°29′~33°07′,地形主要为平原、丘陵、山脉、河流和湖泊,山区主要集中在研究区的西部和南部地区以及湘赣交界处。截至2019年底,研究区共有县级行政区划325个。长江中游城市群由三省(湖北—武汉、湖南—长沙、江西—南昌)的省会城市组成,是中国长江经济带的重要组成部分。2015 年,国务院正式批复《长江中游城市群发展规划》,确定该地区为中部地区经济发展重点省份。但由于各县在研究区内的位置不同,各县之间的经济发展状况存在较大的空间差异。县域经济差距较大,县域经济发展极不平衡。因此,在本研究中,我们选择这三个省份作为研究区域,以探讨这三个省份经济发展状况的差异。由于研究区内各县的位置不同,各县之间的经济发展状况存在较大的空间差异。县域经济差距较大,县域经济发展极不平衡。因此,在本研究中,我们选择这三个省份作为研究区域,以探讨这三个省份经济发展状况的差异。由于研究区内各县的位置不同,各县之间的经济发展状况存在较大的空间差异。县域经济差距较大,县域经济发展极不平衡。因此,在本研究中,我们选择这三个省份作为研究区域,以探讨这三个省份经济发展状况的差异。
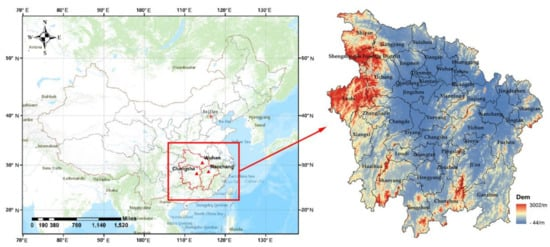
图 1. 研究区域。
2.2. 数据和数据预处理
本次研究中,佩恩公共政策研究所地球观测组提供的2015-2018年NPP-VIIRS月度综合数据共48个阶段和2015-2016年2个阶段的年度NTL数据( https://eogdata. mines.edu/download_dnb_composites.html ), 被选为校准和合成研究区 2018 NPP-VIIRS 年度稳定 NTL 数据。中国2018年合成LJ1-01 NTL数据由湖北数据与应用中心高分辨率对地观测系统提供(高分辨率对地观测系统湖北数据与应用网)。利用2018年6月至12月中国275幅无云LJ1-01影像合成数据,利用夜间灯光影像匹配算法获取连接点,用于与地面控制点的平面区块平差。然后,对所有图像进行正射校正。最后,将所有的夜间光照正射影像镶嵌得到中国夜间光照图[ 33 ]。因此,2018年合成LJ1-01 NTL数据的定位精度得到了提高。本文使用的社会经济统计数据来自各省统计局提供的《2019年统计年鉴》和各县发布的《2018年国民经济和社会发展统计公报》(http://tjj.hubei.gov.cn)。, http://tjj.hunan.gov.cn/, 江西省统计局 )。很少遇到数据缺失的情况,我们使用平均值或相邻年份的数据来替换缺失值。此外,本研究还应用了中国的一些基础地理信息数据,如行政边界、DEM(数字高程模型)、农田生产潜力数据、年平均降水数据和年平均气温数据。行政边界、DEM和农田生产潜力数据集来自中国科学院资源环境数据云平台(http://www.resdc.cn/Default.aspx)。DEM是基于最新的SRTM(Shuttle Radar Topography Mission)V4.1数据经过整理拼接后生成的,其空间分辨率为90 m。以耕地分布、土壤和DEM数据为基础,利用GAEZ(全球农业生态区)模型,综合考虑光照、温度、水分、CO 2浓度、农气候限制和地形。2018年年平均降水量和年平均气温数据是根据月平均数据合成的,数据来源于国家地球系统科学数据中心、国家科技基础设施(http://www.geodata.cn)),空间分辨率约为 1 公里。这两组月度数据是根据CRU(Climatic Research Unit)发布的全球0.5°气候数据集和WorldClim发布的高分辨率气候数据集生成的。在本文和相关的指令施加的数据示于附录A,表A2。
2.2.1. NPP-VIIRS 日期
原始的 NPP-VIIRS 数据不仅包括市区的光照强度,还包括一些背景噪声,如火灾、燃烧的废气和火山爆发[ 34 ]。从原始数据来看,由于背景噪声的影响,NPP-VIIRS 数据中的一些像素为负值。此外,高反射表面,例如雪山,会导致光线较弱的区域的像素值突然增加 [ 35 ]。由于这些问题,原始 NPP-VIIRS 数据必须在用于评估 CEI 之前进行处理。本文采用了 Hu 和 Zhou 提出的合成中国地区 NPP-VIIRS NTL 数据的方法。的数据处理流程如下[ 36,37 ]:
Step 1. 年均图像合成和负值消除。根据式(1),利用2015-2018年的月光照数据合成年光照数据,其中DN i为月复合产品的辐射值,N表示月数,DN j表示平均光照一年的价值。理论上,光辐射值不应小于0;因此,根据2015年标准年度数据替换2015年合成数据中的负值。然后,将 2016-2018 年合成数据中的负值替换为上一年的数据。
DNj=∑我= 1NDN一世N
(1)
步骤 2. 消除不稳定的光源和背景噪音。根据2015年和2016年的标准年度NTL数据,其已经删除了背景噪声,这两个阶段的数据被从浮到整数,的部分转化DN > 0被设置为1,并且部分DN ≤0设置为0,从而得到二值图像。将这两个二值图像相乘得到合成二值图像。DN = 1的部分被识别为没有背景噪声的区域;即2015年和2016年的稳定光源区域。然后以合成二值图像作为标定标准,利用公式(2)提取2015-2018年的稳定光源区域DN表示修正后的年度合成数据中的稳定光源;DN k表示要校正的图像在某一年的稳定光源;和DN K-1表示校正前一年的二值图像为一年稳定的光源。
d ñ={0,DNk - 1= 0 | DN到=0;1,DNk - 1= 1 & DN到=1;,k > 2015
(2)
第三步,高值剔除,持续修正。通过从合成的年度夜间灯光数据中提取亮度值,经过数理统计分析可以得到2015-2018年每年的最大亮度阈值,可以代替高值。按照次年光照亮度值不低于上年的原则,在2015年合成夜间光照数据的基础上,其他年份的数据按公式(式)逐年修正3) 获得2018年可靠的年度夜间光照数据,其中DN为修正后的年度光照亮度值;DN x表示要校正的年光亮度值;和DN x− 1表示上一年修正后的年光亮度值。
d ñ={DNx - 1, DNX≤DNx - 1DNX,DNX>DNx - 1x > 2015
(3)
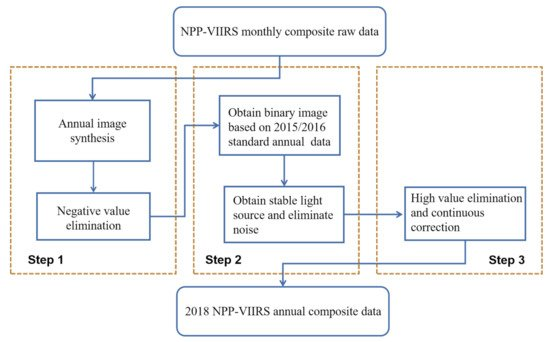
图 2. NPP-VIIRS NTL 数据处理流程。

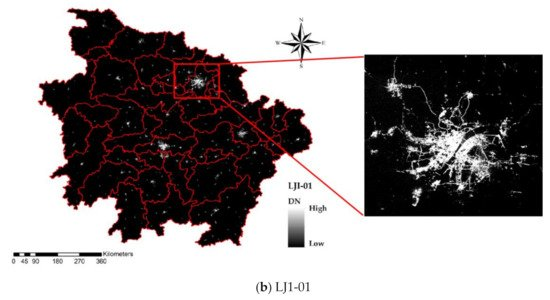
图 3. 研究区处理后的 NTL 数据。红色矩形勾勒出武汉市区。( a ) 处理了 2018 年的 NPP/ VIIRS NTL 数据和 ( b ) 处理了 2018 年的 LJ1-01 NTL 数据。
2.2.2. LJ1-01数据
Nightsat 是一种卫星系统的概念,它能够以适合描绘人类住区主要特征的空间分辨率对夜间灯光的位置、范围和亮度进行全球观测。根据其要求,低光成像数据必须实现具有10分贝[一个信号/噪声比(SNR)最低检测辐射率38,39]。LJ1-01数据的SNR高于35dB;因此,无需从没有负值的 LJ1-01 NTL 数据中去除噪声。然而,应该注意的是,NPP-VIIRS 数据被校准为绝对辐射并提供辐射亮度值。因此,为了确保 NPP-VIIRS 和 LJ1-01 NTL 可以进行比较,需要对 LJ1-01 数据进行绝对辐射校正。在本文中,将LJ1-01 数据的数字 ( DN ) 转换为辐射,以准确分析照明亮度和差异。辐射转换公式如(4)所示,基于实验室校准[ 15 ]。研究区处理后的2018年合成LJ1-01 NTL数据见图3b。
其中DN是每个像素的图像灰度值,L是绝对辐射校正值,单位为W·m -2 sr -1 μm -1。LJ1-01的辐射转换为中心波长,而NPP卫星使用全波段辐射。因此,两类数据的带宽差异导致辐射值的单位不同。为了便于比较,我们将L值乘以带宽进行单位换算。LJ1-01 的辐射范围为 460–980 nm,因此带宽等于 0.52 μm。计算出每个像素的辐射亮度后,单位转换为nW·cm -2 sr -1。
L = DN3/2⋅10−10,
(4)
2.2.3. 社会经济参数标准化
在本研究中,选择了多个社会经济参数来确定每个县的经济发展状况。为了保证各个维度之间的可比性,需要消除各个参数之间的测量差异。因此,根据公式(5)对所选参数进行标准化和归一化。基于所选指标将增加或减少 CEI 的事实,为其分配相应的负面或正面属性。
X一世=⎧⎩⎨⎪⎪⎪⎪⎪⎪X一世−X我敏X我最大−X我敏,(X一世,正)X我最大−X一世X我最大−X我敏,(X一世, NË g ^a t i v和)
(5)
上式中,x i为处理后的无量纲索引值,映射在0和1之间。X i表示原始数据;X i min表示索引i的最小值;和X IMAX代表索引的最大值我。当X i指标属性为正时,采用式(5)中的上式;当X i索引属性为负时,采用(5)中的以下公式。
本研究还应用了具有不同投影坐标系和空间分辨率的多源地理基础数据。为了减少这些差异,我们重新投影和重新采样这些数据。使用ArcGIS 10.4,所有基础地理数据都投影到更适合中国的Albers等积投影坐标系,并重采样到1000 m的空间分辨率,保证空间一致性。考虑到NPP-VIIRS/LJ1-01空间分辨率的差异,本研究仅对其进行Alberts等积坐标投影处理。
2.3. 县域经济指标计算
县域经济是评价城乡社会经济发展的基本单位。针对影响县域经济的因素的多样性和复杂性,可以选取一系列影响县域经济的重要指标来综合评价县域经济的发展水平。由于各学者在建立县域经济评价体系时考虑的视角不同,在体系的层次结构设计和指标的选取上存在一定差异,但核心思想基本一致。指标的选取一般遵循综合性、代表性、可及性和科学效度四项原则,以保证评价结果的真实性和客观性。40 , 41 ],本研究从经济状况、民生、社会发展、公共资源、自然脆弱性五个方面反映了研究区各县的经济发展情况,共20个指标。具体评价指标见表2。
表 2. 用于计算县级经济指数 (CEI) 的评价指标。
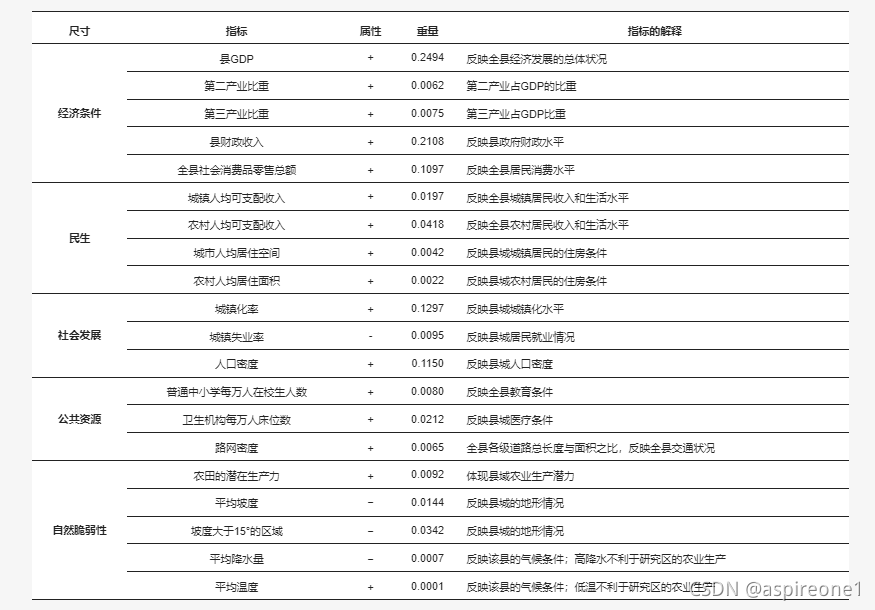

指标权重在评价一个县域多维经济发展中具有重要作用。因此,确定指标权重的过程非常重要。根据上述指标,采用含熵修正的层次分析法(Entropy-AHP)计算各县的CEI。Entropy-AHP 是一种综合加权评价方法。层次分析法(AHP)是一种综合考虑定性和定量分析的多指标综合评价方法,可以根据决策者的意图确定权重;而熵权法(EWM),基于信息熵的定义,客观计算各指标权重,为多指标综合评价提供依据,不受人为干扰。鉴于这两种方法的优缺点,两种方法的结合可以弥补单一方法的不足。具体实施步骤如式(6)-(18)所示。
(1)
AHP 权重的计算。层次分析法将问题分解为不同的因素,并根据它们的相互影响将它们组合成不同的层次,形成多层次的分析结构模型;根据模型确定最低级别相对于最高级别的相对重要性。层次分析法的主要步骤如下:
(一种)
层次分析法判断矩阵A的构建。
A = (一种我Ĵ)n×n
(6)
判断矩阵A的元素a ij表示第i个指标相对于第j个指标的重要性,由Santy的1-9标度法给出[ 42 ],其中1表示两个指标同等重要,3表示表示第i个索引比第j个索引更重要,9 表示第i个索引明显比第j个索引重要。数字越大,第i个索引相对于j 的重要性越高-th 索引。通过使用相同的量表对指标进行主观比较,可以更大程度地降低因属性不同或其他因素造成的评分难度,从而提高判断的准确性。
(二)
单层重量测定。矩阵 A 的归一化特征向量用作权重向量W。w i归一化得到指标的单级权重。
秒我Ĵ=一种我Ĵ/∑k = 1n一种ķ Ĵ,(一种我Ĵ,一种ķ Ĵ∈A)
(7)
ω一世=∑j = 1n秒我Ĵ
(8)
ω一世′=ω一世/∑我= 1nω一世
(9)
(C)
一致性验证。由于判断矩阵的构建来源于主观评分,为了避免逻辑上的矛盾,需要对判断矩阵的一致性进行验证。AHP 使用CI作为一致性验证指标,CR作为一致性比率。计算方法如式(10)和(11)所示,其中λ为矩阵的最大特征值,RI为随机性指数。RI与判断矩阵阶数的关系如表3所示。一般当一致性比CR <0.1时,认为A的不一致性在允许范围内,验证了一致性。
C一世=λ - nn - 1
(10)
CR =C一世RI
(11)
表 3 随机性指数(RI)与判断矩阵阶数的关系。


(四)
AHP 权重测定。每个指标的最终权重可以通过将二级指标权重乘以步骤(b)中获得的对应一级指标权重来计算。
ω一^ h磷-我=ω一世(1)⋅ω一世(2)
(12)
(2)
熵权重计算。利用熵计算各指标的变异系数,确定指标权重,得到客观的综合评价结果。熵权法的主要步骤如下:
(和)
指标同化。
其中 P ij是第j个县数据中第i个指标的无量纲值。
磷我Ĵ=X我Ĵ/∑我= 1米X我Ĵ
(13)
(F)
计算每个指标的熵e i。
和一世=−1ln (米)∑我= 1米磷我Ĵ输入磷我Ĵ
(14)
(G)
计算每个指标g i的变异系数。
G一世=1−和一世
(15)
(H)
计算每个指标的权重。
ω熵=G一世/∑我= 1nG一世
(16)
(3)
熵-层次分析法权重的计算。使用W熵修改W AHP,将结果归一化得到最终的W i。
乙一世=ω层次分析法×ω熵
(17)
在一世=乙一世/∑我= 1n乙一世
(18)
(4)
建设研究区的CEI。根据2.2 节中的 Entropy-AHP 权重和无量纲数据,使用线性加权对这些数据求和。最终根据公式(19)得到研究区各县的CEI。
C和一世=∑一世n在一世X一世
(19)
2.4. RF 回归模型
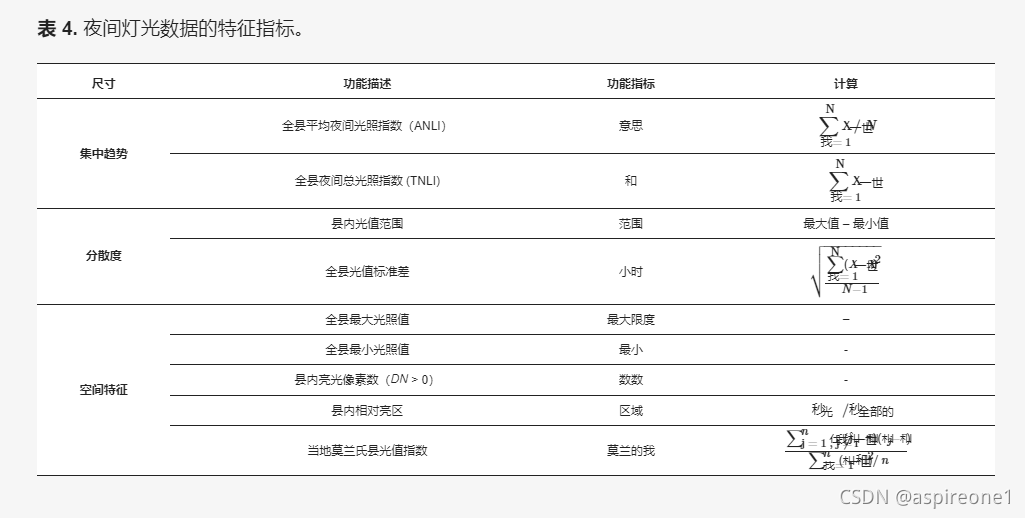
与传统的线性回归数学模型相比,机器学习算法在解决非线性问题和处理高维数据集方面做得更好。本研究提供了一个例子,利用RF算法根据夜间灯光图像的多维特征对CEI进行回归,以提高模型的准确性。根据2.2节得到的处理后的NTL数据,参考文献[ 43 ],从光像素的集中趋势、离散度和空间特征三个方面选取9个特征指标作为数据集的自变量。NTL数据的特征指标如表4所示。
表 4. 夜间灯光数据的特征指标。

随机森林(RF)是一种集成学习方法,它通过组合大量决策树来改进回归树方法[ 29]。它的分类器是CART(Classification And Regression Tree)。当数据集的因变量是连续的时,树算法就是回归树,可以用叶子节点观察到的均值作为预测值来解决回归问题。当数据集的因变量分散时,树算法就是一个分类树,可以用来解决分类问题。RF的主要思想是使用bootstrap抽样方法从原始样本N中提取K个样本集,对每个样本进行决策树建模,然后根据生成的多棵树对数据进行预测。最终预测确定为所有决策树的预测的平均值。分类结果以得票最多的为最终类标签;
与传统的回归算法相比,RF 显示出更高的预测精度,以及无需假设先验概率分布即可对不同变量之间的复杂交互进行建模的能力,以及分析变量重要性的能力 [ 44 ]。RF 回归建模中的主要参数包括估计器的数量、最大特征、最大深度、最小分割样本、最小叶样本等。有关制定的 RF 回归模型的更多详细信息可以在 Breiman [ 29] 中找到]。RF回归模型作为一种监督算法,需要选择样本进行模型训练。本研究采用交叉验证的方法调整模型误差,确定建模过程中的最佳参数设置。平均绝对误差(MAE)和确定系数(R 2)用于表示模型的准确性。公式如下:
其中n是县的数量;CEI t,i为县I的实际值;CEI e,i为县I的估计值;和C和一世¯¯¯¯¯¯¯是各县的实际平均CEI。
电阻2=∑n我= 1( C和一世Ë ,我−C和一世¯¯¯¯¯¯¯)2∑n我= 1( C和一世牛逼,我−C和一世¯¯¯¯¯¯¯)2
(20)
米一è=1n∑我= 1n| C和一世牛逼,我- C和一世Ë ,我|
(21)
为了研究CEI计算模型中各个变量的重要性,进行了变量重要性分析。变量的重要性来自于随机排列变量时模型预测精度的损失[ 29 ]。每个变量的重要性是通过计算变量排列变化时均方根误差增加的百分比来衡量的。较高的百分比表明较大的误差是由变量的随机排列引起的;因此,变量更为重要。
2.5. CEI 的空间分析
“一切都与其他一切有关,但近的事物比远的事物更相关”[ 45 ]。空间依赖性是促成自然界秩序、模式和多样性的重要来源之一 [ 46 ]。定量测量地理对象空间关联特征的方法有很多。全局空间关联指数包括 Moran's I、Geary's C、Getis's G 和 join count [ 47 , 48 ]。局部空间关联指数包括局部 Moran's I、LISA(空间关联局部指标)和 Getis's G* [ 49 ]。本研究选用Moran's I和LISA对研究区CEI空间格局进行定量分析,是有效可行的。
(1)
Moran's I. Moran's I 用于测量全局空间自相关。它是一个加权相关系数,用于检测空间随机性的偏离,可以指示空间模式。计算方法如式(22)[ 48 ]所示,其中x i和x j分别为空间点i 和j 处的值;X¯是整个区域内所有点的平均值;w ij是空间邻域关系的权重;n 为研究区内所有空间统计单元的总数。Moran's I 的范围是 [–1,1]。正值表示对象在空间上呈正相关,负值表示对象在空间上呈负相关。Moran's I 的统计显着性可以通过标准归一化后的 Z 分数来评估。
我 =n∑我= 1n∑j = 1n在我Ĵ( x一世−X¯) ( xj− X¯)∑我= 1n∑j = 1n在我Ĵ⋅∑我= 1n( x一世− X¯)2
(22)
(2)
丽莎。Moran's I 只能测量整个区域的空间相关性;在空间异质性的情况下,它不能反映每个分区的空间聚类。1995 年,美国区域经济学家 Anselin 提出了 LISA(空间关联的局部指标)统计量来评价给定变量的空间排列中是否存在集群[ 49 ]。该统计数据检测局部空间关联并可用于识别局部聚类(即相邻区域具有相似值的区域)或空间异常值(即与其相邻区域不同的区域)。LISA 统计量的计算如公式(23)所示,其中 x i、x j和 w ij意义同(22)。LISA 统计将 Moran's I 分解为每个位置的贡献。所有观测值的 I i总和与 Moran's I 成正比。
一世一世=n ( x一世− X¯)∑j = 1n在我Ĵ( xj− X¯)∑j = 1n( xj− X¯)2
(23)
3. 结果
3.1. 研究区域的 CEI 映射
本研究基于2.3提出的方法,得到2018年湖北、湖南、江西各县的CEI。根据CEI值的统计分布,采用分位数分类法将CEI分为五类:较低(CEI ≤ 0.078)、低 (0.078 < CEI ≤ 0.112)、中 (0.112 < CEI ≤ 0.149)、高 (0.149 < CEI ≤ 0.219) 和更高 (CEI > 0.219)。绘制了2018年湖北、湖南、江西的CEI分布图,结果如图4所示。
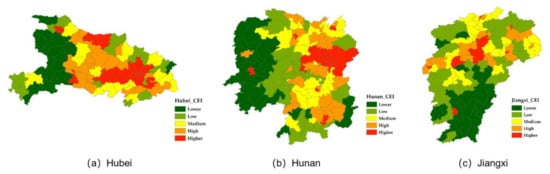
Figure 4. CEI distribution maps of Hubei, Hunan, and Jiangxi in 2018.
总体来看,2018年湖北、湖南、江西三省各县的CEI值呈现出相同的分布格局:高值区域主要集中在省会及周边城市群。但是,县域之间的发展水平存在明显的不平衡。湖北省中部县的CEI明显高于西部和东部地区。湖南省CEI值高的地区主要分布在长沙市南北两侧,CEI向西逐渐降低。江西省CEI值高的地区主要集中在北部,以南昌为中心,而CEI值低的地区主要分布在南部。第 3.3 节。
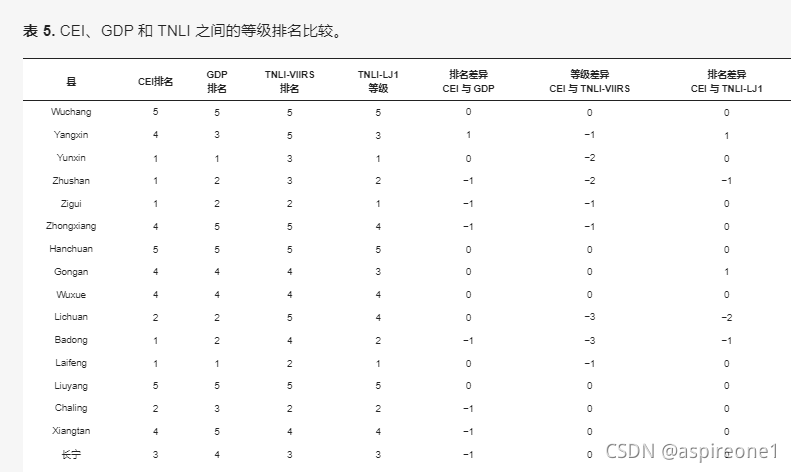
为检验CEI对经济发展评价的有效性,本研究从数据集中随机抽取32个样本县,按照相同的分类方法将样本县的GDP和TNLI划分为5个等级,比较各县之间的等级差异。 CEI、GDP 和 TNLI。表 5珠山、巴东、慈利、涟源等经济发展评价标准较为综合,样本县的排名存在一定差异。大多数抽样县的CEI排名低于各自的GDP排名,这主要是由于地势恶劣、物质资金匮乏、交通不便和医疗条件差。因此,与GDP等单维度经济参数相比,多维度指标评价更能全面反映一个县的经济状况。同时我们发现,与NPP-VIIRS数据相比,总体而言,LJ1-01 TNLI等级与CEI的差异较为温和,所有绝对值均不超过2。
表 5. CEI、GDP 和 TNLI 之间的等级排名比较。

3.2. 模型结果和准确性
我们随机选取研究区70%的县(共325个县)作为训练集,其余30%的县作为测试集,训练拟合RF模型。经过参数优化,得到最终的拟合结果。为了验证RF在估计县级多维经济发展方面的优势,我们还使用了LR模型进行比较。图 5显示了来自统计数据的真实 CEI 与通过采样县的 LR 和 RF 模型估计的预测 CEI 之间的散点图。表 6比较了 LR 和 RF 的模型精度。以LJ1-01 NTL数据为例,LR模型中回归R 2为 0.638,MAE 为 0.0056;而在 RF 模型中,回归 R 2为 0.8168,MAE 为 0.0027。可以看出,LR模型的性能与RF算法相比是比较差的。后者对数据多重共线性不太敏感,在描述涉及多个变量的复杂非线性关系时具有鲁棒性[ 50 ];因此,可以获得更好的性能。同时,在 RF 模型中,R 2LJ1-01 数据的值(0.8168)高于 NPP/VIIRS 数据的值(0.7245);结果表明,LJ1-01数据与CEI的相关性明显高于等效的NPP/VIIRS数据。为了尽量减少训练集造成的误差的影响,我们进行了 10 次交叉验证。结果还表明,LJI-01的R 2 (RF模型中的0.7920)高于NPP-VIIRS的R 2 (RF模型中的0.7054)。也就是说,LJ1-01数据具有更大的建模潜力,这主要是由于辐射值范围更广,以及这些数据具有更高的空间分辨率和更详细地反映夜间社会活动的能力。
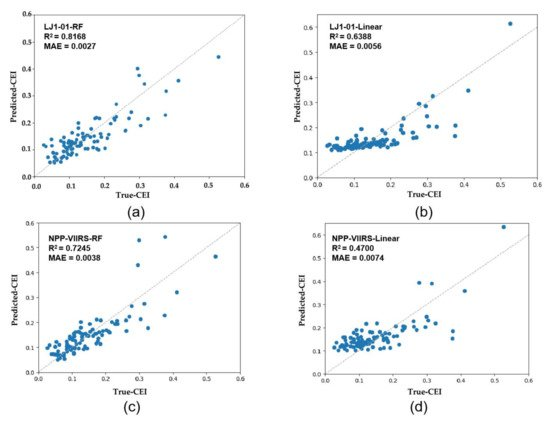
图 5. 真实 CEI 和预测 CEI 之间的散点图。( a ) 使用 LJ1-01 NTL 的射频模型;( b ) LR 型号使用 LJ1-01 NTL;( c ) 使用 NPP-VIIRS NTL 的 RF 模型;( d ) 使用 NPP-VIIRS NTL 的 LR 模型。
表 6. LR 和 RF 模型之间的精度比较。
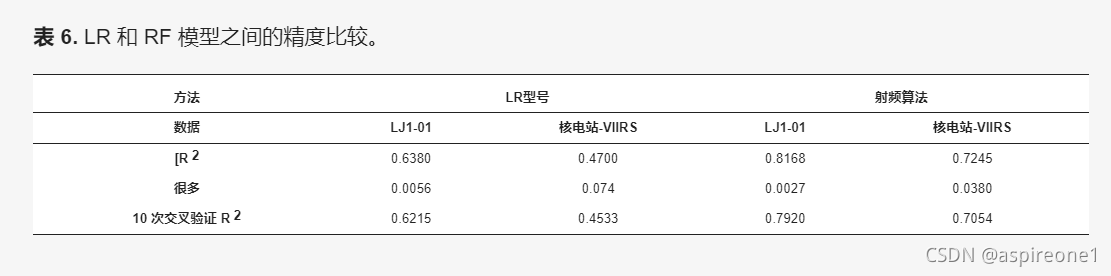

所选变量按其在 RF 模型中的重要性排序,如表 7和图 6 所示. 在 LJ1-01 RF 模型中,最重要的变量是 AREA,重要性值为 0.3445。COUNT、ANLI、TNLI 和 MORAN'S I 也很重要,值都大于 0.1,而在 NPP-VIIRS RF 模型中,最重要的变量是 STD,为 0.4681,其次是 TNLI 和 AREA,它们是值大于 0.1 的仅有的其他两个变量。一般来说,经济发展较好的县,夜光面积的范围会更大,而在经济发展均衡的县,发光像素的分布会更均匀。与 NPP-VIIRS 数据相比,LJ1-01 数据具有更多的图像特征,在 RF 模型中的重要性相对较高。变量重要性排序表明,与 NPP-VIIRS 数据相比,LJ1-01数据的图像特征可以更好地应用于RF模型,提高CEI的识别精度。无论是在 LJI-01 还是 NPP-VIIRS RF 回归模型中,RANGE、MAX 和 MIN 的重要性值都比较小,尤其是在 LJ1-01 RF 模型中。这可能是因为大多数县的 MIN 值非常小,导致 RANGE 和 MAX 值之间的差异很小。
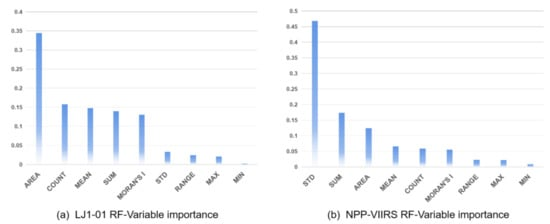
图 6. RF 模型中九个变量的重要性:( a ) LJ1-01 NTL 和 ( b ) NPP-VIIRS NTL。
表 7. RF 模型中 LJ1-01 和 NPP-VIIRS 的每个变量的重要性。


为了进一步验证应用CEI估算县域经济发展的优势,我们还使用RF模型对样本县的GDP进行回归,发现R 2与CEI回归结果相比降低;结果如表8所示。图 7显示了 CEI 和 GDP 的 RF 回归模型的散点图。以LJ1-01 NTL数据为例,回归R 2CEI(0.8168)的值显着高于GDP(0.6858)的值,说明与从抽样县中选取GDP相比,使用多维指标评价县域经济发展更为科学可靠。除此之外,结果更符合NTL遥感数据的图像特征。此外,可以发现回归 R 2LJ1-01 数据的 GDP 值(0.6858)高于 NPP/VIIRS 数据的 GDP 值(0.6451)。结果还表明,LJ1-01 数据在社会经济参数估计方面在一定程度上优于 NPP-VIIRS 数据。相应地,利用LJ1-01数据来检测县域经济发展是一种更可行、更可靠的方法。NTL数据评估的多维县级经济指标为政府相关部门提供了科学依据,可为未来社会经济发展战略提供良好的参考。
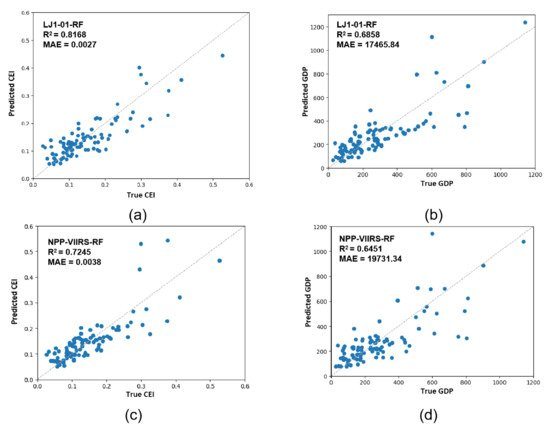
图 7. CEI 和 GDP 的 RF 回归模型散点图: ( a ) 使用 LJ1-01 NTL 数据预测 CEI;( b ) 使用 LJ1-01 NTL 数据预测 GDP;( c ) 使用 NPP-VIIRS NTL 数据预测 CEI;( d ) 使用 NPP-VIIRS NTL 数据预测 GDP。
表 8. RF 模型回归 CEI 和 GDP 的准确性比较。


3.3. CEI 的空间分析
本研究使用Moran's I和LISA分析了湖北、湖南和江西三省CEI的分布情况。三个省份的 Moran's I 值如表 9所示。三个省的Moran's I值均大于0,并已通过假设检验。结果表明,三省的CEI分布呈现正空间相关性。湖北省的 Moran's I 最高,为 0.7125。该省各县经济发展极不平衡,江西省莫兰氏Ⅰ度较小,为0.4976。全省各县呈现比较均衡的发展态势。
表 9. 湖北、湖南和江西省的 Moran's I 值。


图 8显示了湖北、湖南和江西三省 CEI 值的 LISA 统计数据。总体来看,三省的高聚集区集中在省会城市周边的都市圈。同时,各省也呈现出各自的CEI分布特点。湖北省低低聚集区主要集中在省西部(包括恩施、宜昌西部和十堰南部,地理环境较差,不利于经济发展)和黄冈武汉东部城市,发展有限,社会物资匮乏。在湖南省,低低聚集区主要集中在湖南省西南部,包括湘西自治区、怀化西南、邵阳和永州南部。这些地区还受自然条件和物资短缺的影响,发展较为缓慢。此外,怀化市中心城区河城区呈现高低聚集,表明怀化市的发展重点主要集中在中心城区。与周边县域相比,该地区的发展明显不平衡。在江西省,低矮聚集区主要集中在位于省南部的赣州市。除了都市圈以外,以南昌为中心,伊春市和新余市东部还有另外两个高高聚集区,
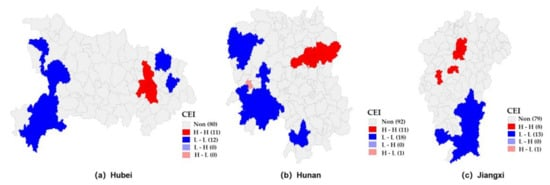
图 8 湖北、湖南和江西 CEI 的空间关联局部指标 (LISA)。
4。讨论
在本研究中,LJ1-01 和 NPP-VIIRS 数据是夜间光照强度的重要信息来源,并对其检测国家级经济发展的潜力进行了调查。通过RF回归模型和LR回归模型进行对比,验证了机器学习算法在夜间灯光数据应用中的可行性和优势。两种NTL数据的比较表明,LJ1-01数据在建模多维社会经济指标方面比NPP-VIIRS数据具有更高的准确性和潜力(表6和表8))。这主要是由于LJ1-01数据提供了更高的空间分辨率,比NPP-VIIRS数据更好地捕捉了人工照明更精细的空间细节,导致夜间社会活动的更详细特征。空间分辨率的提高使LJ1-01数据与参考数据呈现出更加一致的县域经济发展空间格局。此外,与 NPP-VIIRS 数据相比,LJ1-01 图像的晕染现象较少。先前的研究表明,与 DMSP-OLS 复合材料相比,NPP-VIIRS 数据提高了空间分辨率并减少了光晕[ 51 ]。同样,我们发现 LJ1-01 与 NPP-VIIRS 复合材料相比具有相同的优势。根据 Elvidge 等人的研究。[ 52],开花效应会导致对城市经济参数的高估。因此,LJ1-01 夜间灯光图像具有更强的探测经济发展的能力。这一结论也可以通过本研究中得到的变量的重要性排序来验证(图6)。与NPP-VIIRS图像相比,RF回归模型可以更好地识别LJ1-01图像中亮区的特征和亮区的像素数;此外,LJ1-01 图像中县光像素的最小值的重要性最小。图 9以人类活动少、NTL强度低的典型区域武汉长江水体为例,比较NPP-VIIRS和LJ1-01的光辐射值。NPP-VIIRS在长江中的辐射值均超过0,而LJ1-01的辐射值为0,尤其是在长江中心。这一发现为以后的研究提供了参考。

图 9. ( a ) LJ1-01 数据和 ( b ) NPP-VIIRS 数据在水域的比较。
此外,本文还分析了湖北、湖南和江西三省的县域经济格局。对三个省份分别实施了相同的回归方法。结果如表10所示。湖北省的准确度最高(R 2 = 0.8610 使用 LJ1-01 NTL 对湖北的 CEI 进行回归;R 2= 0.8388 使用 NPP-VIIRS NTL 回归湖北的 CEI)。由于各县之间经济发展差距较大,湖北省CEI值范围较广(0.0246~0.7513),更适合检测CEI与夜间光照影像的关系。此外,湖北省县域经济发展总体水平较高;因此,CEI 和 NTL 数据之间的相关性更紧密。
表 10.湖北、湖南和江西省 RF 回归 (R 2 )的准确性。


综上所述,LJ1-01数据可以作为建立社会经济指标模型评价县域经济的有效工具。尽管如此,也承认LJ1-01 NTL数据的应用仍然存在一些限制。首先,由于 LJ1-01 的光谱带通,LJ1-01 的蓝色灵敏度在 460 nm 处降低,这将错过蓝泵白光 LED 450 nm 特征中的一部分光谱功率。因此,LJ1-01 很难看到一些短波长的贡献,例如来自白光 LED 发射的蓝光,这可能会影响实验结果。其次,2018年6月之前的图像是空的,这在一定程度上限制了这些数据在时间序列分析中的应用,尤其是对城市动态相关的历史信息的分析。第三,LJ1-01 数据包含轻微的地理参考误差,限制了这些数据在空间分析中的直接和准确应用。高精度几何校正的预处理对于LJ1-01 NTL减少几何定位误差至关重要。尽管本文应用的中国 2018 年合成 LJ1-01 NTL 数据提高了定位精度,但该数据仅包含单幅图像,无法进行长时间序列分析。最后,部分 LJ1-01 图像的质量还受到云层和月光的影响,这将导致遥感应用出现错误。高精度几何校正的预处理对于LJ1-01 NTL减少几何定位误差至关重要。尽管本文应用的中国 2018 年合成 LJ1-01 NTL 数据提高了定位精度,但该数据仅包含单幅图像,无法进行长时间序列分析。最后,部分 LJ1-01 图像的质量还受到云层和月光的影响,这将导致遥感应用出现错误。高精度几何校正的预处理对于LJ1-01 NTL减少几何定位误差至关重要。尽管本文应用的中国 2018 年合成 LJ1-01 NTL 数据提高了定位精度,但该数据仅包含单幅图像,无法进行长时间序列分析。最后,部分 LJ1-01 图像的质量还受到云层和月光的影响,这将导致遥感应用出现错误。
5。结论
LJ1-01是新一代NTL卫星,空间分辨率更高,数据免费。其 NTL 图像在研究社会经济问题方面具有巨大潜力。本研究以LJ1-01和NPP-VIIRS卫星获取的夜间光照数据为数据源,对湖北、湖南、江西三省各县的经济发展情况进行探测。通过选取多维经济指标,采用熵-层次分析法计算县级经济指数(CEI)。然后,通过使用 LR 和 RF 回归模型探索 CEI 和 NTL 图像之间的关系。结果表明,与传统的线性回归算法相比,RF算法可以显着提高模型的精度。此外,与使用 NPP-VIIRS 数据的回归结果相比,LJ1-01 数据估计的结果具有更高的确定系数,表明 LJ1-01 数据在估计社会经济参数方面的潜力有所提高。本研究还对湖北、湖南、江西三省的CEI空间格局进行了检测,发现湖北省在三省中发展水平最高、发展最不平衡,进一步证明了县域夜间灯光成像的可行性和效率。经济发展水平评价。总之,本研究证实,结合机器学习算法,LJ1-01数据在检测县级经济发展方面具有巨大潜力。本研究还对湖北、湖南、江西三省的CEI空间格局进行了检测,发现湖北省在三省中发展水平最高、发展最不平衡,进一步证明了县域夜间灯光成像的可行性和效率。经济发展水平评价。总之,本研究证实,结合机器学习算法,LJ1-01数据在检测县级经济发展方面具有巨大潜力。本研究还对湖北、湖南、江西三省的CEI空间格局进行了检测,发现湖北省在三省中发展水平最高、发展最不平衡,进一步证明了县域夜间灯光成像的可行性和效率。经济发展水平评价。总之,本研究证实,结合机器学习算法,LJ1-01数据在检测县级经济发展方面具有巨大潜力。
在未来的研究中,LJ1-01夜间影像与其他卫星遥感影像或精细尺度社会经济属性等多源数据的融合,可能为准确识别人类活动提供更多可能。除了 RF 回归模型,更多的机器算法,如 SVM 和高斯过程,可以应用于使用 LJ1-01 数据的未来研究。此外,由于LJ1-01影像还存在光谱带通限制、几何定位误差、月光和云层影响等具有挑战性的问题,需要进一步研究以提高广谱数据的质量。应用。