人群归因分数（Population Attributable Fraction, PAF）：概念、简单计算案例

专注系列化、高质量的R语言教程

本篇目录如下：

1 人群归因分数
- 1.1 相对风险度
- 1.2 人群归因分数
2 案例
- 2.1 示例数据
- 2.2 计算案例1
- 2.3 计算案例2
- 2.4 计算案例3
3 总结

1 人群归因分数

人群归因分数（Population Attributable Fraction, PAF）是疾病负担研究中常用的指标，其大致含义是，假设人群的风险暴露降低至理想水平，预计可减少的患病人口数占实际患病人口数的比例。

The population attributable fraction (PAF), which represents the proportion of risk that would be reduced in a given year if the exposure to a risk factor in the past were reduced to an ideal exposure scenario.^[1]

风险因素的理想暴露水平有多种定义方式，常用的是理论最小风险水平（Theoretical Minimum Risk Level，TMREL），指理论上能使疾病负担水平达到最低的暴露水平。如世卫组织推荐的不会造成健康风险的污染物临界指标^[2]：

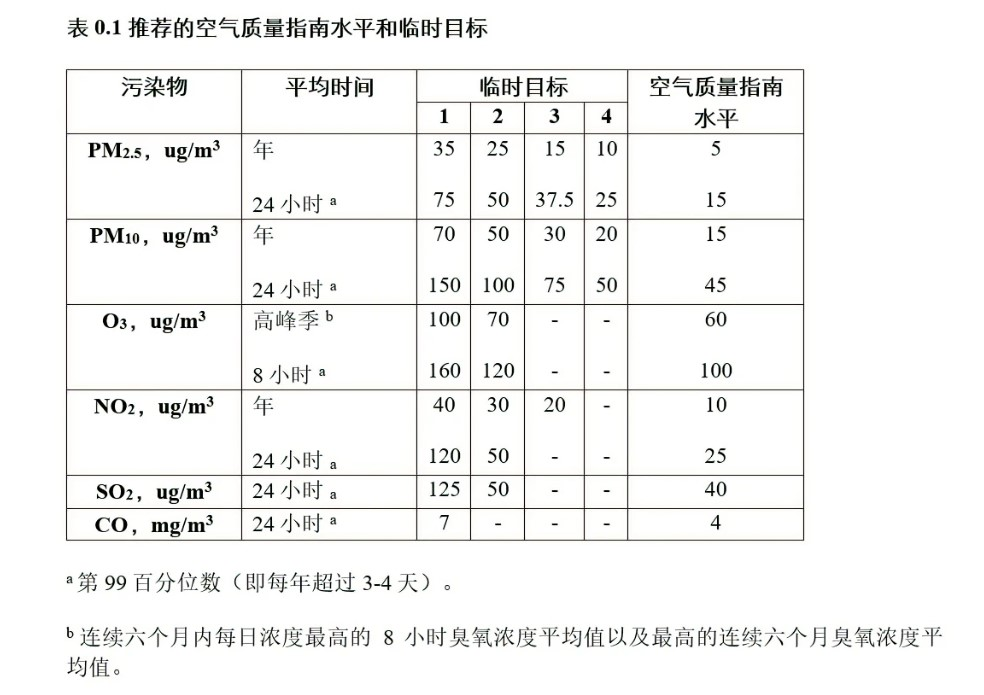
1.1 相对风险度

假设理想暴露水平时的患病人口比例为，暴露水平为时的患病人口比例为，则该暴露水平的相对风险度（Relative Risk，RR）为：

1.2 人群归因分数

如果暴露水平是分类变量，，暴露在各水平的人群比例使用表示，则人群归因分数（PAF）可表示为：

是指理想暴露水平的相对风险度，一般说来它应该是1。不过相对风险度并不一定需要使用本队列的数据进行计算，也可以直接使用或汇总已有的研究成果，这时不一定为1。

如果暴露水平是连续变量：

2 案例

本节通过几个例子展示PAF的具体计算过程。

2.1 示例数据

示例数据使用causalPAF工具包的数据集strokedata。该数据集包括16623个观察样本，本案例涉及到的变量有：

case：二分变量，数值型；0表示未患病，1表示患病；
phys：二分变量；因子类型；1表示缺乏锻炼，2表示积极锻炼。

根据后文需要，将phys转换为0/1变量。需要注意的是，phys的类别顺序为“2、1”，因此转换后0表示积极锻炼、1表示缺乏锻炼。

library(causalPAF)
data = strokedata  
levels(data$phys)
## [1] "2" "1"

data$phys <- as.numeric(data$phys) - 1
unique(data$phys)
## [1] 1 0

2.2 计算案例1

以phys为分组变量，展示样本的分布情况：

library(tidyverse) 
table <- data %>%
  group_by(phys) %>%
  summarise(pop = length(case),
            pop_prop = pop/16623,
            case_num = sum(case),
            case_prop = mean(case))

table
##    phys   pop pop_prop case_num case_prop
##   <dbl> <int>    <dbl>    <dbl>     <dbl>
## 1     0  2297    0.138     1043     0.454
## 2     1 14326    0.862     7192     0.502

pop：样本数；
pop_prop：样本占总样本比例；
case_num：患病样本数；
case_prop：患病率，即case_num/pop。

显然，可以将phys = 0定义为理想暴露水平，计算phys = 0,1时的相对风险度：

rr0 = 1
(rr1 = table$case_prop[2]/table$case_prop[1]) 
## [1] 1.105609

phys = 0,1时的人口暴露比例即pop_prop：

p0 = table$pop_prop[1]
p1 = table$pop_prop[2]

套用上节的计算公式，计算PAF：

1 - rr0/(rr0*p0 + rr1*p1)
## [1] 0.08342266

因此，由缺乏锻炼（phys = 1）导致的患病人群归因分数为8.34%。

2.3 计算案例2

上节是使用公式计算PAF，也可以直接使用PAF的定义来计算，即若所有样本的phys都取0（理想暴露水平），预计可减少的患病人口数占实际患病人口数的比例。

可减少的患病人口数reduce即phys = 1的样本数乘以两个暴露水平的患病率之差：

(reduce <- table$pop[2]*(table$case_prop[2] - table$case_prop[1])) 
## [1] 686.9856

实际患病人口数total_case：

(total_case = sum(data$case))
## [1] 8235

reduce与total_case之比即PAF：

reduce/total_case
## [1] 0.08342266

与2.2节计算结果一致。

2.4 计算案例3

在该类研究中，响应变量通常都是0/1二分变量，因此一般可使用Logistic回归进行建模。

以case为响应变量，phys为解释变量（风险因子），建立Logistic模型：

fit <- glm(case ~ phys, data = data,
           family = binomial())
summary(fit)
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.18424    0.04191  -4.396 1.10e-05 ***
## phys         0.19233    0.04512   4.263 2.02e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

使用回归结果估计在理想暴露水平phys = 0时的患病率：

newdata <- data.frame(phys = 0)
(p0 <- predict(fit, newdata = newdata, type = "response"))
## 0.4540705

使用PAF定义的计算公式：

就是实际人群患病比例，因此上式可简化为：

(p = mean(data$case))
## [1] 0.4953979

1 - p0/p
## 0.08342266

AF工具包的AFglm()函数以广义回归模型为输入对象计算PAF：

library(AF)
AFglm(fit, exposure = "phys", data = data)
## Estimated attributable fraction (AF) and standard error : 
## 
##          AF  Std.Error
##  0.08342266 0.01948951

3 总结

本篇推文简要介绍了PAF、RR的概念及其计算公式，使用的案例只涉及一个风险变量，后续推文会介绍有控制变量、多风险变量及中介变量（mediator）的情况。

参考资料

[1]

GBD:2017 补充材料1，p33: https://doi.org/10.1016/S0140-6736(18)32225-6

[2]

环境（室外）空气质量和健康: https://www.who.int/zh/news-room/fact-sheets/detail/ambient-(outdoor)-air-quality-and-health