判断点是否在扇形内解法探究 C++实现
面试时遇到了这个问题,在游戏开发中,类似于检测扇形技能是否命中了敌人。
我当时的第一想法是先通过扇形半径平方和玩家和敌人的距离平方大小比较,提前检测出一批不符合条件的敌人。如果玩家和敌人的距离平方小于扇形半径平方的话,再通过一些算法判断。
算法判断的第一想法是求出与x轴的夹角,然后判断夹角是否在扇形的两个边的夹角内。然后想了想觉得可以类比判断点是否在三角形内,通过叉乘判断。
下来以后参考了别人的一些思路,又自己进行了一些总结,并用C++测试了一下,希望帮到读者,有任何问题欢迎批评指正。
首先是最经典的通过给定玩家朝向(即扇形的中心向量)和技能的角度大小来判断是否命中。为了简化问题,我们假设扇形角度大小小于180度。同时为了不在扇形半径平方和玩家和敌人的距离平方大小比较时就筛选了过多的点,而导致之后的判断算法运行时间不易比较,将扇形的半径设置大一点。
#include <iostream>
#include <cmath>
using namespace std;
const int n = 100, m = 100; // 用离散点模拟敌人,n行m列
bool table[n][m];
void func(int x, int y, int r, int orieX, int orieY, float angle) {
float len = sqrt(orieX * orieX + orieY * orieY);
int rPow = r * r;
for (int ex = 0; ex < n; ex++)
for (int ey = 0; ey < m; ey++) {
int dx = ex - x;
int dy = ey - y;
int lenPow2 = dx * dx + dy * dy;
if (lenPow2 > rPow)
continue;
int dotRes = orieX * dx + orieY * dy; // 获取点乘
if (dotRes < 0)
continue;
float angle2 = acos(dotRes / (len * sqrt(lenPow2))); // 通过点乘获取夹角
if (angle2 * 2 > angle)
continue;
table[ex][ey] = true;
}
}
int main() {
int x, y, r; // 玩家位置(x,y)技能半径r
int orieX, orieY; // 玩家朝向(orieX,orieY)
float angle; // 技能总角度
cin >> x >> y >> r; // eg: 20 20 100 1 1 1.57
cin >> orieX >> orieY >> angle;
func(x, y, r, orieX, orieY, angle);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++)
cout << (table[i][j] ? "*" : "-");
cout << endl;
}
return 0;
}
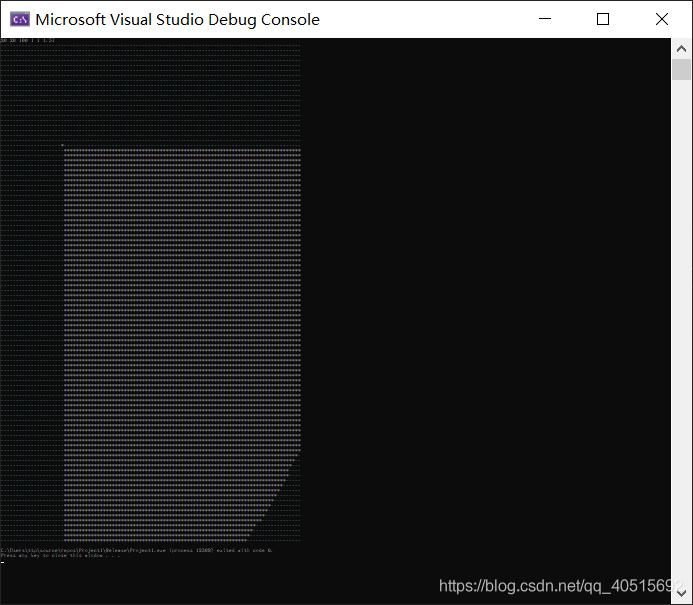
输入20 20 100 1 1 1.57表示在(20,20)处有一个玩家朝向为(1,1)角度大小为pi/2,半径100的扇形技能,运行结果如下:
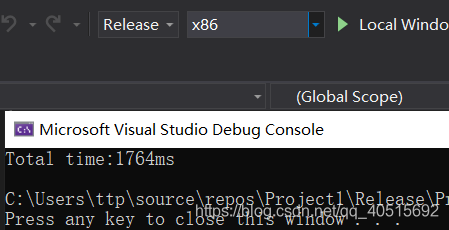
我们再测试一下性能,10000*10000的点计算在x86 release下耗时1764ms:
#include <iostream>
#include <cmath>
#include <ctime>
using namespace std;
const int n = 10000, m = 10000;
bool table[n][m];
void func(int x, int y, int r, int orieX, int orieY, float angle) {
float len = sqrt(orieX * orieX + orieY * orieY);
int rPow = r * r;
for (int ex = 0; ex < n; ex++)
for (int ey = 0; ey < m; ey++) {
int dx = ex - x;
int dy = ey - y;
int lenPow2 = dx * dx + dy * dy;
if (lenPow2 > rPow)
continue;
int dotRes = orieX * dx + orieY * dy;
if (dotRes < 0)
continue;
float angle2 = acos(dotRes / (len * sqrt(lenPow2)));
if (angle2 * 2 > angle)
continue;
table[ex][ey] = true;
}
}
int main() {
int x, y, r;
int orieX, orieY;
float angle;
// 在(20,20)处有一个玩家朝向为(1,1)角度大小为pi/2,半径n的扇形技能
x = 20,y = 20,r = n;
orieX = 1,orieY = 1,angle = 1.57;
clock_t start,end;
start=clock(); //程序开始计时
func(x,y,r,orieX,orieY,angle);
end=clock(); //程序结束用时
double endtime=(double)(end-start)/CLOCKS_PER_SEC;
cout<<"Total time:"<<endtime*1000<<"ms"<<endl; //ms为单位
return 0;
}
第二种方法是通过给定玩家的技能的两边方向(需指出左边界和右边界,不能随便给出顺序,左右是相对与玩家朝向定义的),原因就是我们要通过叉乘进行快速判断。
先给出叉乘的右手定则:
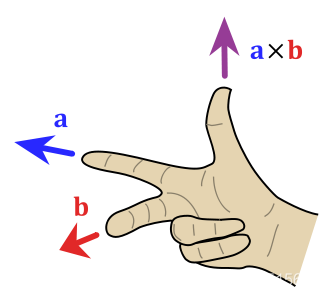
假设左边界为a,敌人方向为b,那么叉乘结果为正,此时表示敌人并不在扇形边界内,同理假设右边界为a,敌人方向为b,那么叉乘结果为负,表示敌人并不在扇形边界内。
#include <iostream>
#include <cmath>
using namespace std;
const int n = 100, m = 100;
bool table[n][m];
void func(int x, int y, int r, int orieXl, int orieYl, int orieXr, int orieYr) {
int rPow = r * r;
for (int ex = 0; ex < n; ex++)
for (int ey = 0; ey < m; ey++) {
int dx = ex - x;
int dy = ey - y;
int lenPow2 = dx * dx + dy * dy;
if (lenPow2 > rPow)
continue;
int crossRes1 = orieXl * dy - dx * orieYl;
if (crossRes1 > 0)
continue;
int crossRes2 = orieXr * dy - dx * orieYr;
if (crossRes2 < 0)
continue;
table[ex][ey] = true;
}
}
int main() {
int x, y, r;
int orieXl, orieYl;
int orieXr, orieYr;
cin >> x >> y >> r; // eg: 20 20 100 0 1 1 0
cin >> orieXl >> orieYl >> orieXr >> orieYr;
func(x,y,r,orieXl,orieYl,orieXr,orieYr);
for(int i=0;i<n;i++){
for(int j=0;j<m;j++)
cout << (table[i][j]?"*":"-");
cout << endl;
}
return 0;
}
输入20 20 100 0 1 1 0表示在(20,20)处有一个扇形技能,边界为左边向量(0,1)、右边向量(1,0),半径100的扇形技能。结果如下:

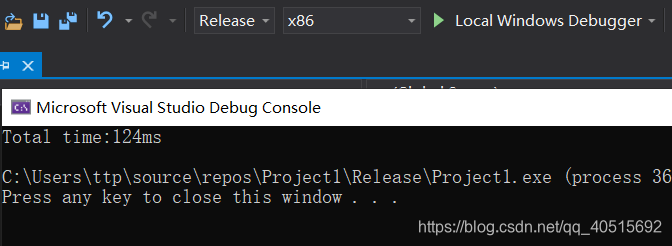
我们再测试一下这个的性能,10000*10000的点计算在x86 release下耗时124ms:
#include <iostream>
#include <cmath>
#include <ctime>
using namespace std;
const int n = 10000, m = 10000;
bool table[n][m];
void func(int x, int y, int r, int orieXl, int orieYl, int orieXr, int orieYr) {
int rPow = r * r;
for (int ex = 0; ex < n; ex++)
for (int ey = 0; ey < m; ey++) {
int dx = ex - x;
int dy = ey - y;
int lenPow2 = dx * dx + dy * dy;
if (lenPow2 > rPow)
continue;
int crossRes1 = orieXl * dy - dx * orieYl;
if (crossRes1 > 0)
continue;
int crossRes2 = orieXr * dy - dx * orieYr;
if (crossRes2 < 0)
continue;
table[ex][ey] = true;
}
}
int main() {
int x, y, r;
int orieXl, orieYl;
int orieXr, orieYr;
// 在(20,20)处有一个扇形技能,边界为左边向量(0,1)、右边向量(1,0),半径n的扇形技能
x = 20, y = 20, r = n;
orieXl = 0, orieYl = 1, orieXr = 1, orieYr = 0;
clock_t start, end;
start = clock(); //程序开始计时
func(x, y, r, orieXl, orieYl, orieXr, orieYr);
end = clock(); //程序结束用时
double endtime = (double)(end - start) / CLOCKS_PER_SEC;
cout << "Total time:" << endtime * 1000 << "ms" << endl; //ms为单位
return 0;
}
通过上面的结果可以看出,在一定的条件下,方法2的速度快不少。但是我想了下有几个限制,第一是游戏开发的话,多给出的是玩家朝向和技能角度大小(应该吧),这样需要在使用方法2时先通过玩家朝向和技能角度大小求出扇形的两个边界,然后再运行,这也引出第二个问题就是方法2没有涉及浮点运算,所以非常快,但是如果给定的数据为浮点数,速度势必会降一点(测试了下,并没有下降多少)。
所以还是需要具体问题具体分析,我认为如果检测目标过多,可以先求出扇形的两个边界然后用方法2,有任何问题欢迎批评指正。