三角形外接球万能公式_立体几何一类题的两个秒杀公式

895a38670081fa073f0d8c21a0dda8e5.png

立体几何一类题的两个秒杀公式

大家好,我又回来了.

欢迎关注:[1点数学]

本文摘要:

1. 双半径单交线公式及其证明

2. 公共边两对角公式

3. 两个公式的应用

今天给大家介绍立体几何中两个公式,

这两个公式的使用条件是:

存在两个平面互相垂直.

具体内容请看下面的图片.

如果你想获得本文的文档,请{关注}+{点赞}+{转发},然后私信我,或者在文章后面留言.

正文开始:

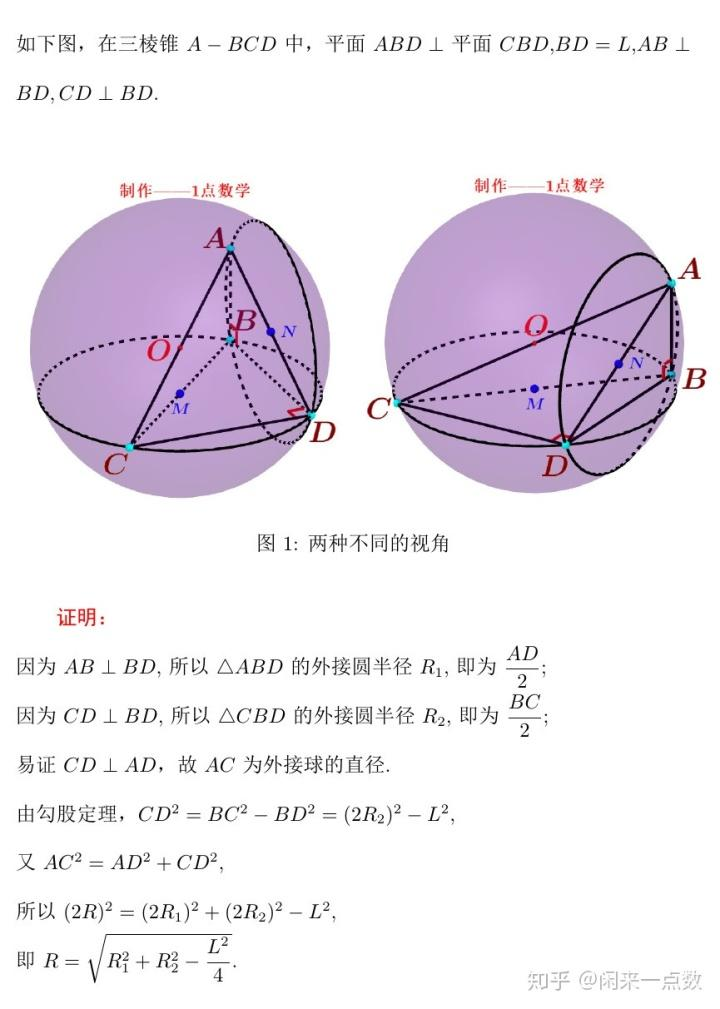
双半径单交线公式

若相互垂直的两凸多边形的外接圆半径分别为R_1,R_2，两外接圆公共弦长为L,则由两凸多边形顶点连接而成的几何体的外接球半径： R=√[R_1^2+R_2^2- (L^2)/4].

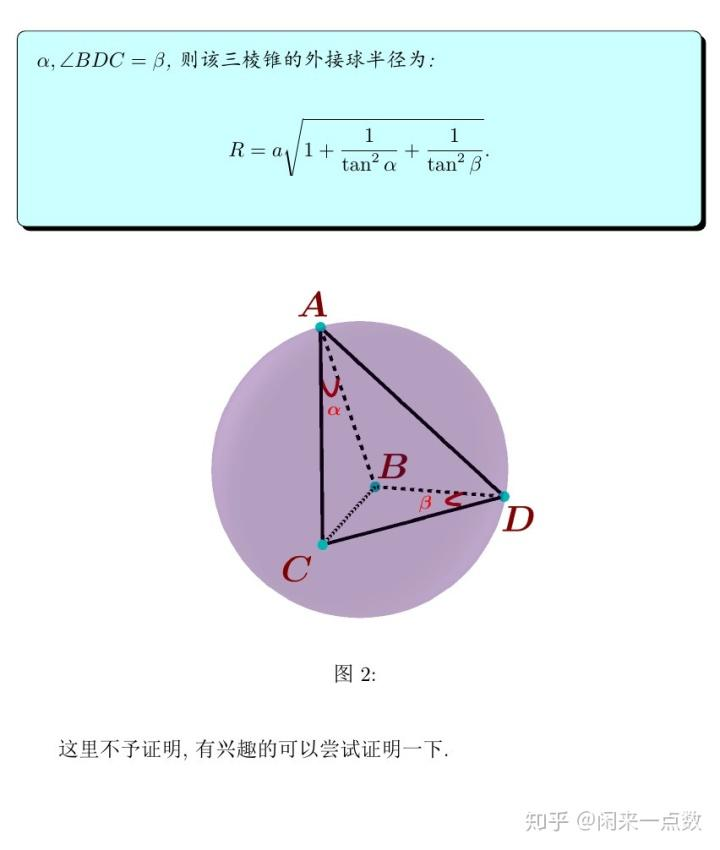
公共边两对角公式

若相互垂直的两凸多边形(存在外接圆)公共边的长度为a,公共边(弦)在两凸多边形内所对的圆周角分别为α,β,则由两凸多边形顶点连接而成的几何体的外接球半径： R=a√(1+1/tan^2α+1/tan^2β).

def4f633033002ddb195d612de1cf833.png

0b3d169b94195f85ff1d7b42f25d82f7.png

80dd70847283efc8f8eefd8768d038cb.gif

c8c08d9c8015da65958f29d4f57b9ba8.png

32bf69d0d2b9ab52369c091814c128bd.png

d8a6a20dd1af0f91f8ac4391ba488437.png

e737d4e133d7f106381a5355aaa6eae4.png

5c17cf3d2edaac163565df18b5534804.png

感谢大家的观看,如有疑问请留言.

感谢大家的支持,如果喜欢的话就点个赞吧~