概率论与数理统计 | (12) 极大似然估计

目录

1. 极大似然估计

2. 估计量的评价准则，无偏性

3. 有效性，均方误差

1. 极大似然估计

极(最)大似然估计的原理介绍

假设在一个罐中放着许多白球和黑球，并假定已经知道两种球的数目之比是1:3，但不知道哪种颜色的球多。如果用放回抽样方法从罐中取5个球，观察结果为:黑、白、黑、黑、黑，估计取到黑球的概率p.

离散型总体：

连续型总体：

说明：

1）未知参数可能不是一个，设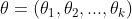 $\theta = (\theta_1,\theta_2,...,\theta_k)$ 。

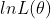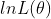2）求 $L(\theta)$ 的最大值时，可转换为求 $ln L(\theta)$ 的最大值， $ln L(\theta)$ 称为对数似然函数

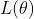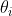3）若 $L(\theta)$ 关于某个 $\theta_i$ 是单调增(减)函数，则 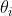$\theta_i$ 的极大似然估计为 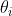$\theta_i$ 的最大(小)值（与样本有关）

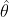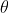4）若 $\hat{\theta}$ 是 $\theta$ 的极大似然估计，则 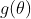$g(\theta)$ 的极大似然估计为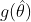 $g(\hat{\theta})$

例题

2. 估计量的评价准则，无偏性

从前之前的学习中可以看到，对总体的未知参数可用不同方法求得不同的估计量，如何评价不同估计量的好坏?

常用的评价准则有以下四条：

1）无偏性准则

2）有效性准则

3）均方误差准则

4）相合性准则

无偏估计量

无偏性的统计意义是指在大量重复试验下，由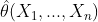 $\hat{\theta}(X_1,...,X_n)$ 给出的估计的平均恰好是 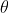$\theta$ ,从而无偏性保证了 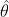$\hat{\theta}$ 没有系统误差。

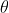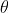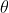例如，工厂长期为商家提供某种商品，假设生产过程相对稳定，产品合格率为 $\theta$ ，虽然一批货的合格率可能会高于 $\theta$ 或低于 $\theta$ ，但无偏性能够保证在较长一段时间内合格率接近 $\theta$ ，所以双方互不吃亏。但作为顾客购买商品，只有二种可能，即买到的是合格品或不合格品，此时无偏性没有意义。

例题

根据之前学习的内容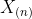， $X_{(n)}$ 的分布函数为：

纠偏方法

3. 有效性，均方误差

有效性准则

方差较小的无偏估计量是一个更有效的估计量。

例题

均方误差准则

4. 相合性

相合性准则