深度学习--第10篇: Pytorch卷积层,池化层,线性层和激活函数层

1. 卷积层 Conv Layer

1.1 卷积 1d/2d/3d

 定义:
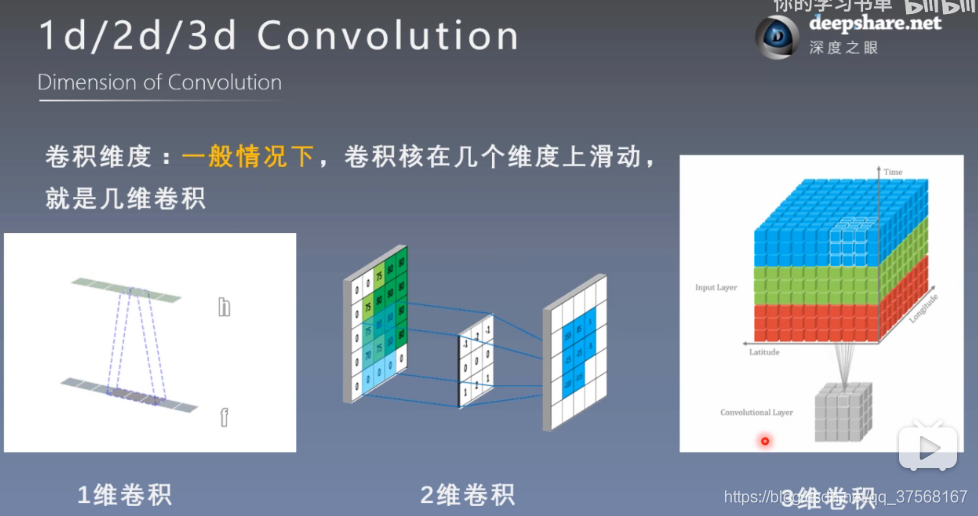
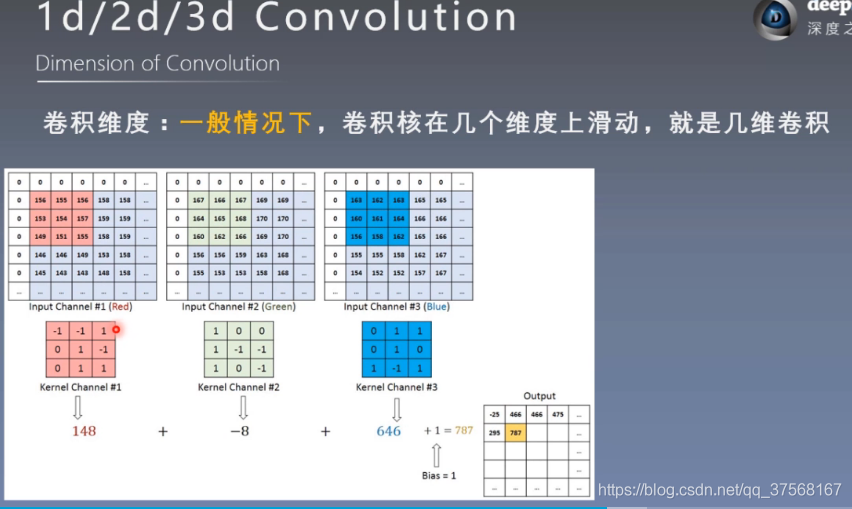
 - 卷积运算：卷积核在输入信号（图像）上滑动，相应位置上进行乘加;
 - 卷积核：又称为滤波器，过滤器，可认为是某种模式，某种特征;
 - 卷积维度：一般情况下，卷积核在几个维度上滑动，就是几维卷积
功能:
	卷积过程类似于用一个模板去图像上寻找与他相似的区域，与卷积核模式越相似，激活值越高，从而实现特征提取;

1.2 nn.Conv2d

nn.Conv2d  功能：对多个二维信号进行二维卷积
主要参数(包含默认值)：
    　in_channels：输入通道数
    　out_channels：输出通道数，等价于卷积核个数
    　kernel_size：卷积核尺寸
    　stride=1：步长
    　padding=0：填充个数
    　dilation=1：空调卷积大小
    　groups=1：分组卷积设置
    　bias=True：偏置
    　padding_mode='zeros': 填充模式

• 图像尺寸计算公式:

参数:

• 输入图片大小 Input*Input
• Filter(卷积核)大小 f*f
• 空调卷积大小 d
• 步长 Step
• padding(填充)的像素数p，p=1就相当于给图像填充后图像大小为(input+1) *(input+1)
• 输出图片的大小 output * output

注意: 对于计算不能得到整数的输出结果,采用np.floor 向下取整处理.

简化版:
$$Output=\frac{Input-f+2p}{Step}+1$$

完整版:
$$Output=\frac{Input+2p-d\times (f-1)-1}{Step}+1$$

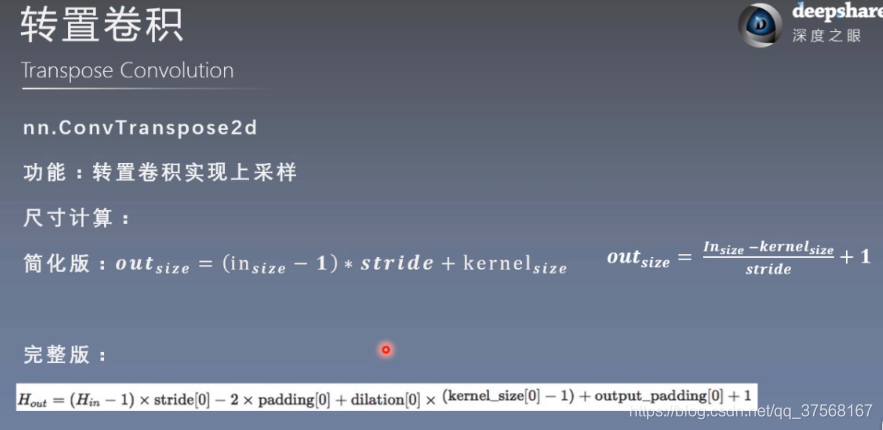
1.3 转置卷积 nn.ConvTranspose

转置卷积又称反卷积和部分跨越卷积，用于对图像进行上采样.

2. 池化层 Pooling Layer

池化运算：对信号进行“收集”并“总结”，类似水池收集水资源，因而得名池化层
“收集”：多变少   “总结”：最大值/平均值

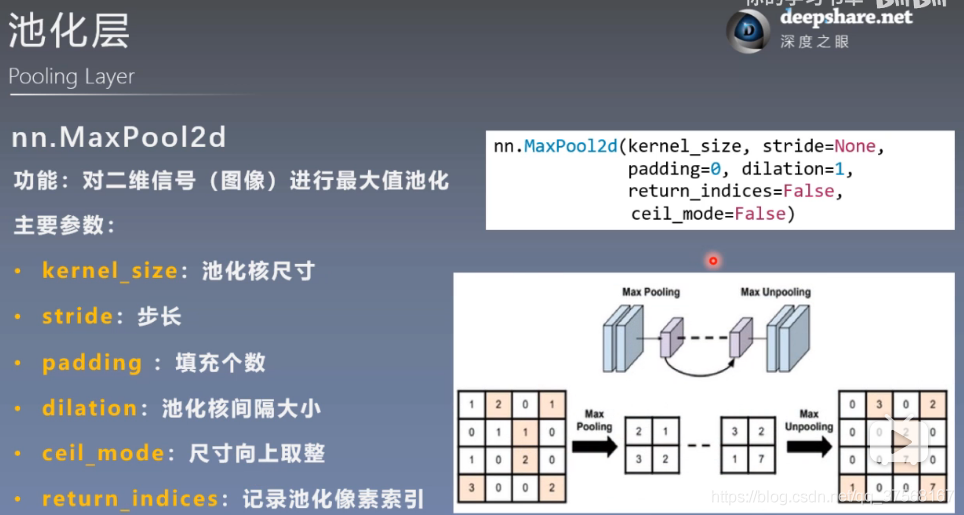
2.1 最大池化 nn.MaxPool2d

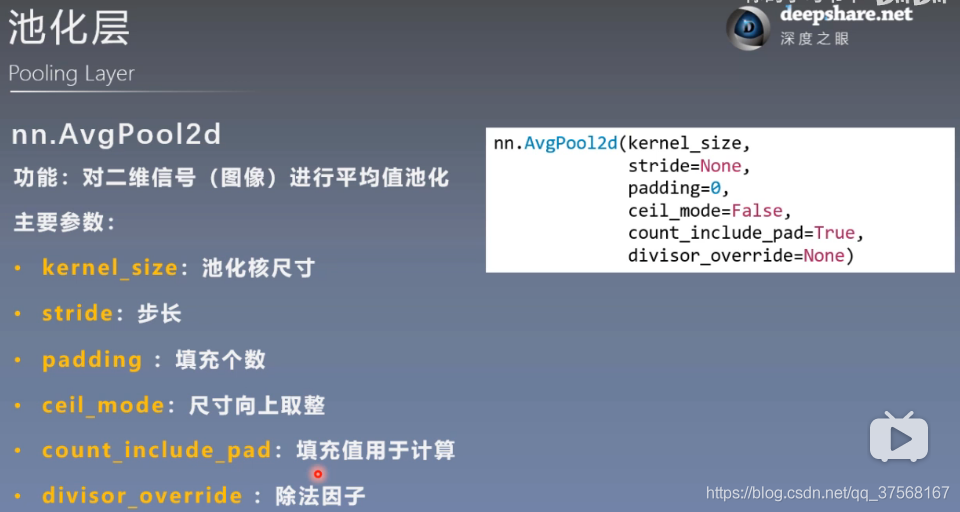
2.2 平均值池化 nn.AvgPool2d

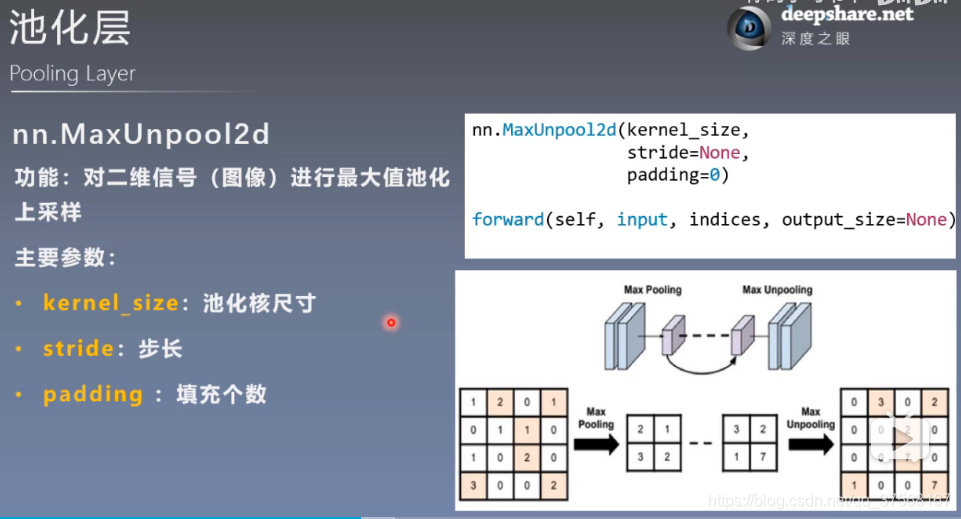
2.3 最大池化上采样 nn.MaxUnpool2d

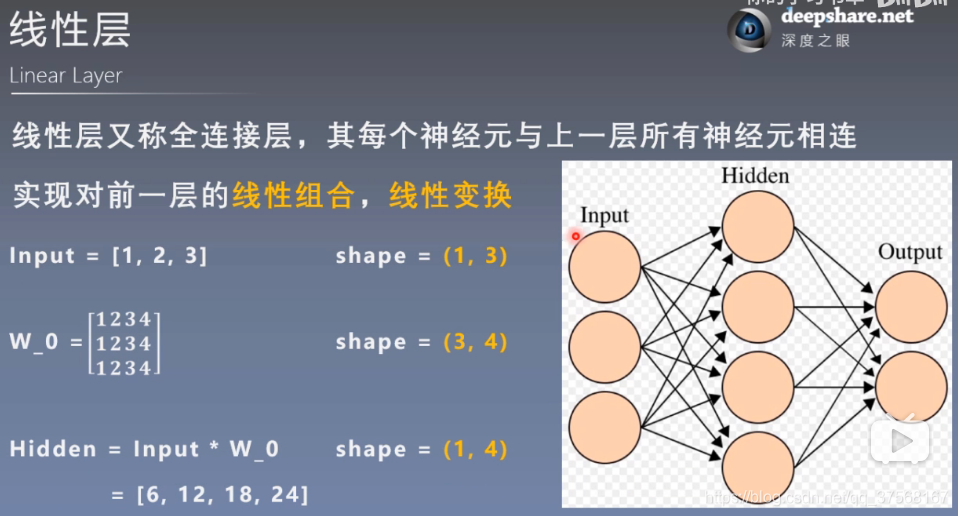
3. 线性层 Linear Layer

线性层又称全连接层，其每个神经元与上一层所有神经元相连实现对前一层的线性组合，线性变换.

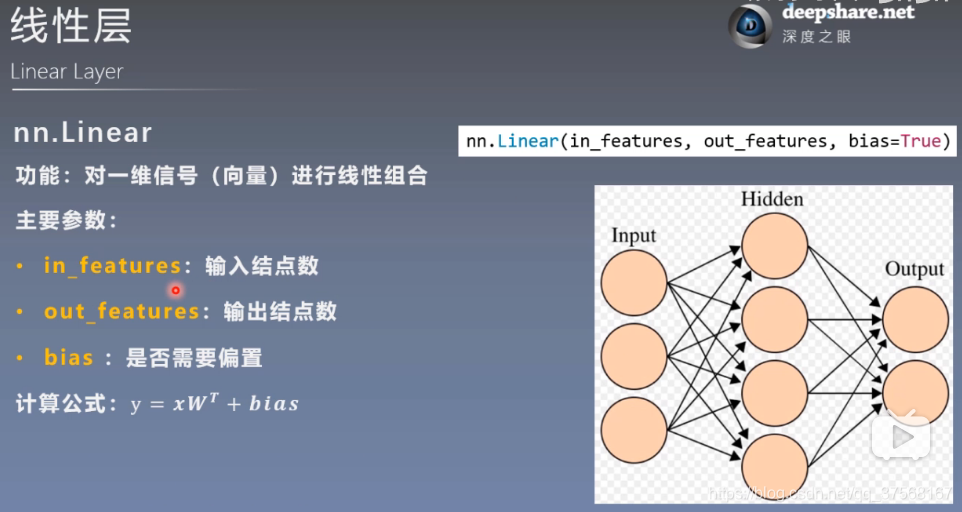
nn.Linear(in_features, out_features, bias=True) 
功能：对一维信号（向量）进行线性组合
主要参数：
    　in_features：输入结点数
      out_features：输出结点数
      bias：是否需要偏置

4. 激活函数层 Activation Layer

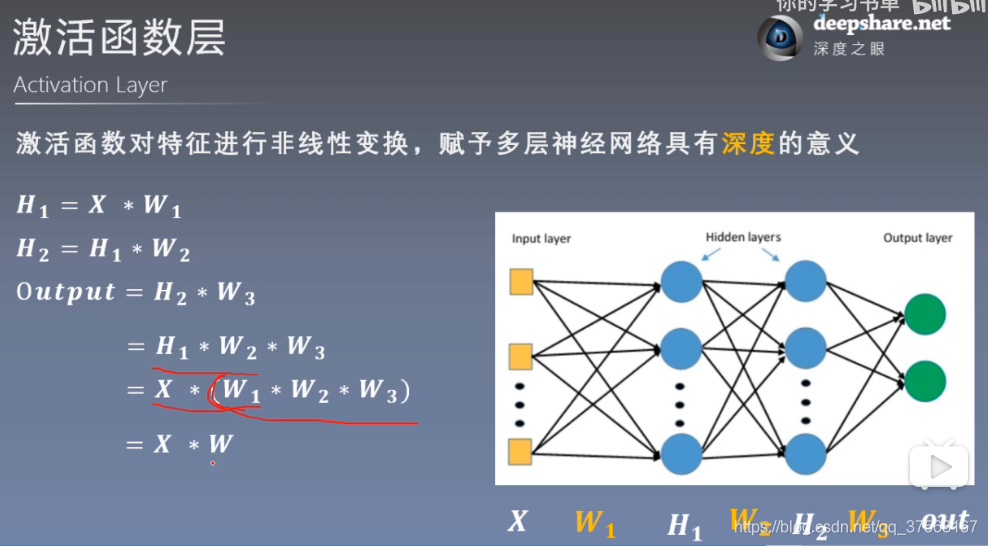
激活函数对特征进行非线性变换，赋予多层神经网络具有深度的意义.

没有激活函数的多个线性层连接,相当于单个线性层.
H1 = X * W1
H2 = H1 * W2
Output = H2 * W3
            = H1 * W2 * W3
            = X * （W1 * W2 * W3）
            = X * W

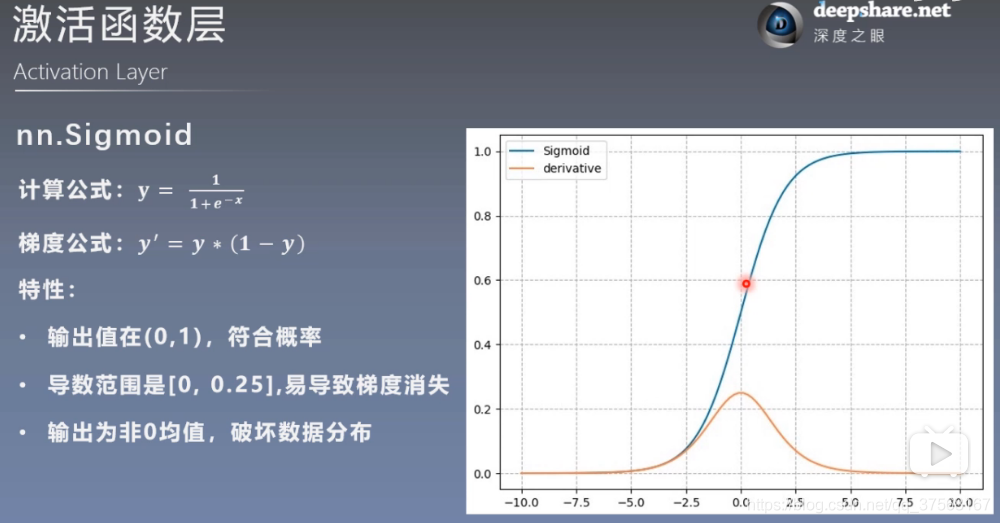
4.1 nn.Sigmoid

特性：
    输出值在（0,1），符合概率
    导数范围是[0， 0.25]，易导致梯度消失
    输出非零均值，破坏数据分布

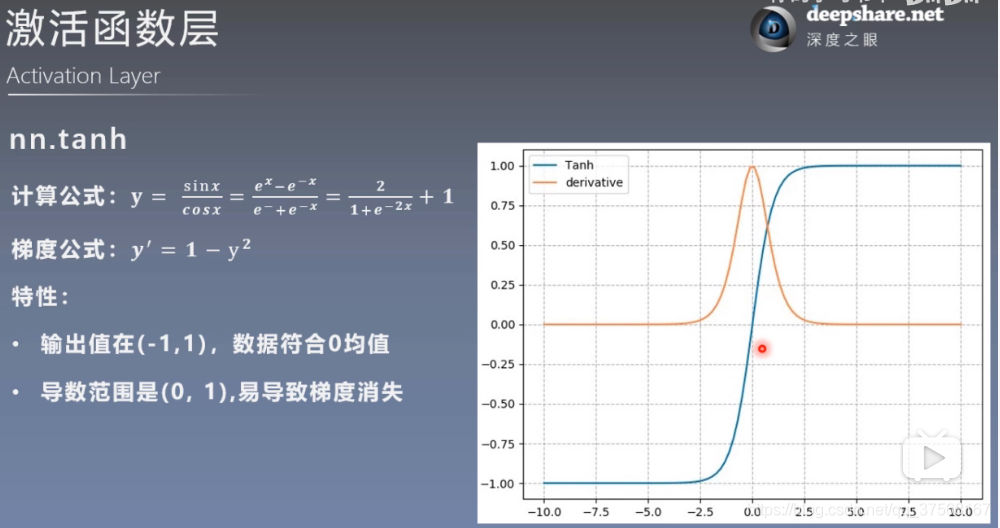
4.2 nn.tanh

特性：
    输出值在（-1,1），数据符合0均值
    导数范围是（0,1），易导致梯度消失

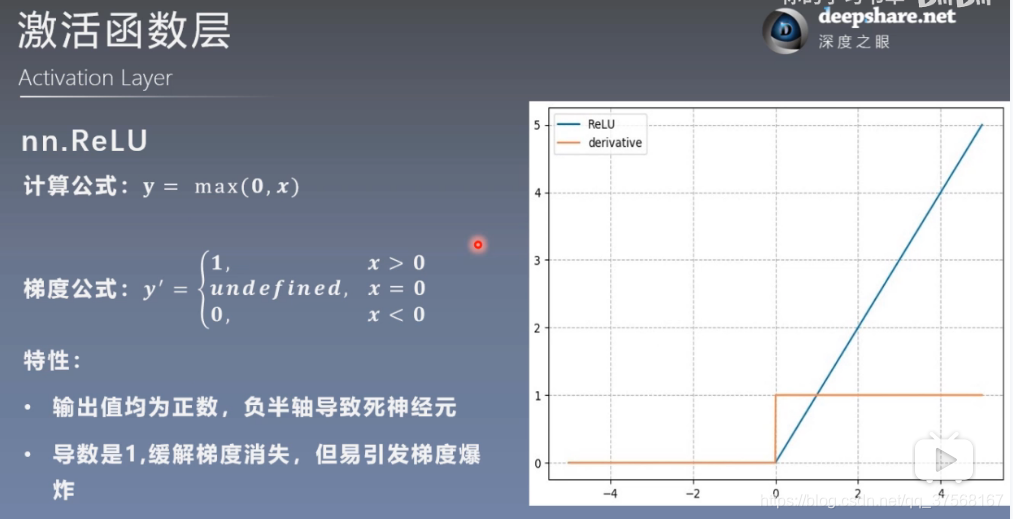
4.3 nn.ReLu

特性：
  　　输出值均为正数，负半轴导致死神经元
     导数是1，缓解梯度消失，但易引发梯度爆炸

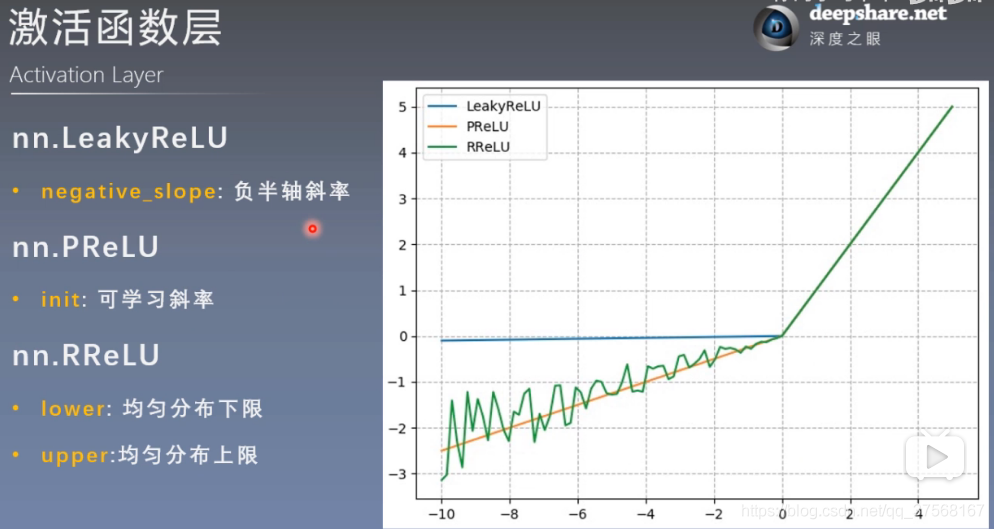
4.4 其他激活函数

5. 正则化

torch.nn.Dropout(p=0.5, inplace=False)
功能: 随机性失活
参数:
	p:被舍弃的概率,失活概率,默认0.5

6. 批量标准化

nn.BatchNorm1d(feature_in)
nn.BatchNorm2d(feature_in)
nn.BatchNorm3d(feature_in)

参数:
	feature_in: 特征数量,2维一般特指特征深度的数量