时间序列分析（2）| ARMA模型的（偏）自相关函数

自相关函数和偏自相关函数是判断ARMA模型平稳性和阶数的有效工具。

1 自相关函数

根据平稳性的定义，与的方差相同，协方差仅与时间间隔有关，那么二者之间的相关系数也就仅与有关了。因为与对应的是同一个变量，所以它们之间的相关系数称为自相关系数。

1.1 AR(1)过程

AR(1)过程的形式如下：

可以计算出它的方差，协方差，从而自相关系数。

也是AR(1)的特征方程的根，由平稳性条件可知，须有。

因此，呈指数型衰减。

基础包stats中的acf()函数可以画出时间序列数据自相关函数（autocorrelation function, ACF）的图象。

acf(x, lag.max = NULL,
    type = c("correlation", "covariance", "partial"),
    plot = TRUE, na.action = na.fail, demean = TRUE, ...)

  • x：时间序列数据；

  • lag.max：时间间隔的最大值；

  • type：绘制的图形类型；correlation表示绘制自相关函数图，covariance表示绘制自协方差函数图，partial表示绘制偏自相关函数图。

如下，分别构造和时的AR(1)过程（截距不影响自相关系数，假设其为0.2）：

set.seed(123)
epsilon = rnorm(200)
y1 = y2 = rep(0,200)

for(i in c(2:200)){
  y1[i] = 0.2 + 0.9*y1[i-1] + epsilon[i]
  y2[i] = 0.2 - 0.9*y2[i-1] + epsilon[i]
}
y1 = y1[51:200]
y2 = y2[51:200]

par(mfrow = c(2,1),
    plt = c(0.15,0.99,0.15,0.9))
plot(y1, type = "l")
plot(y2, type = "l")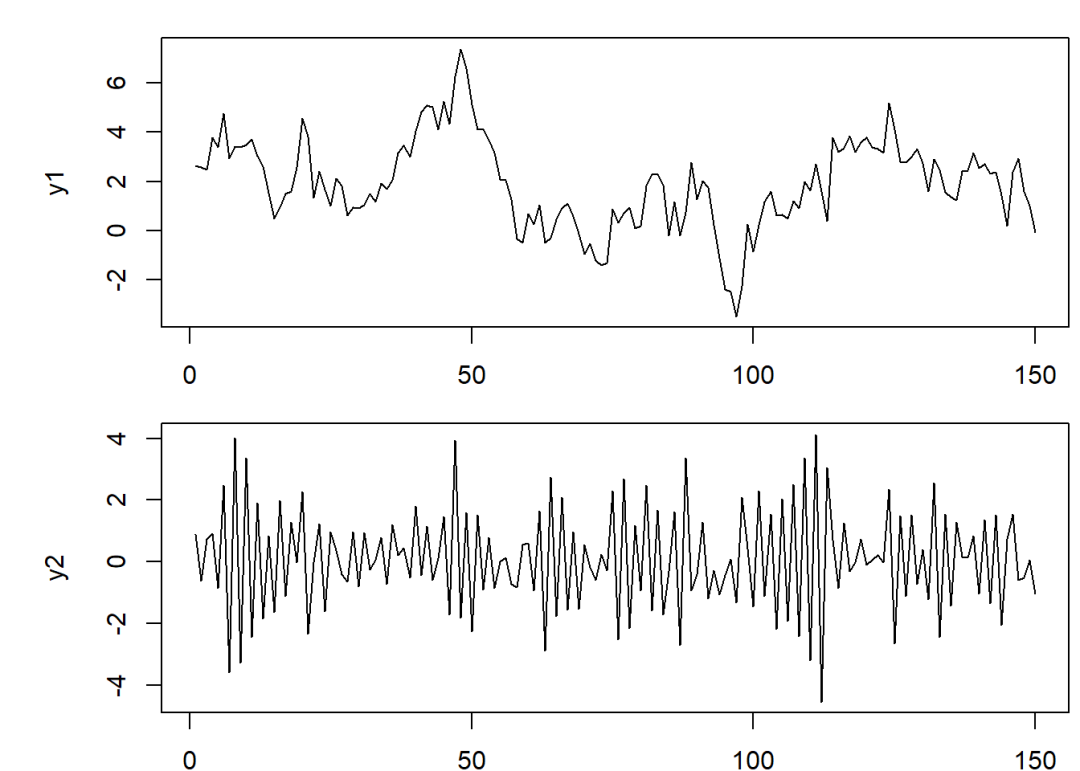
2777696af74478eeeba55a3b011d1623.png

  • 上篇介绍过，AR过程平稳要求事件的起点发生在较早以前（即趋于无穷），因此这里删除了生成的前50个数据，即y = y[51:200]；

  • 两种情况下，图象都呈现震荡走势，没有明显的增长或衰减趋势。

par(mfrow = c(2,1),
    plt = c(0.15,0.99,0.15,0.9))
acf(y1)
curve(0.9^x, 0, 20, add = T, col = "red")
acf(y2)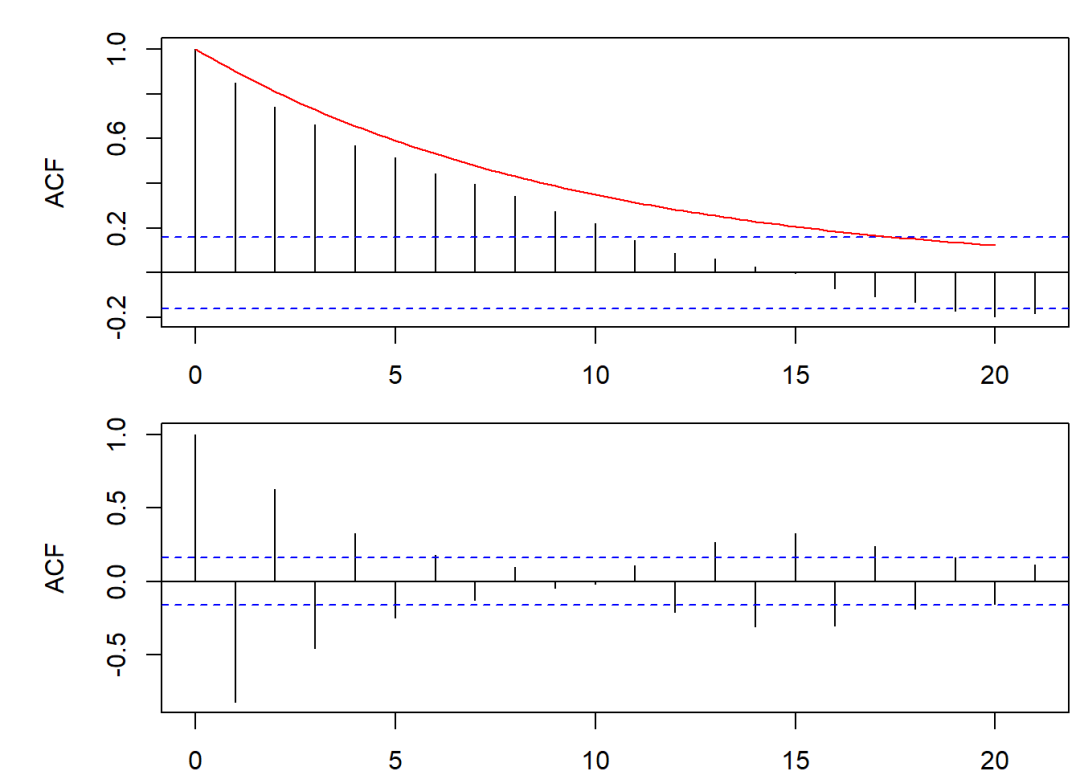
776d926dbd2e29d5e39d9faa4f4a1101.png

  • 上图中的红线表示的函数图象；

  • 蓝色虚线中间的值可以认为不显著区别于0；

  • AR()的自相关函数图象的特点：$0

如下，构造和时的AR(1)过程作为对比：

y3 = y4 = rep(0, 200)
for(i in c(2:200)){
  y3[i] = 0.2 + y3[i-1] + epsilon[i]
  y4[i] = 0.2 + 1.1*y4[i-1] + epsilon[i]
}
y3 = y3[51:200]
y4 = y4[51:200]

par(mfrow = c(4,1),
    plt = c(0.15,0.99,0.2,0.9))
plot(y3, type = "l")
acf(y3)
curve((1/1)^x, 0, 20, add = T, col = "red")

plot(y4, type = "l")
acf(y4)
curve(1.1^(-x), 0, 20, add = T, col = "red")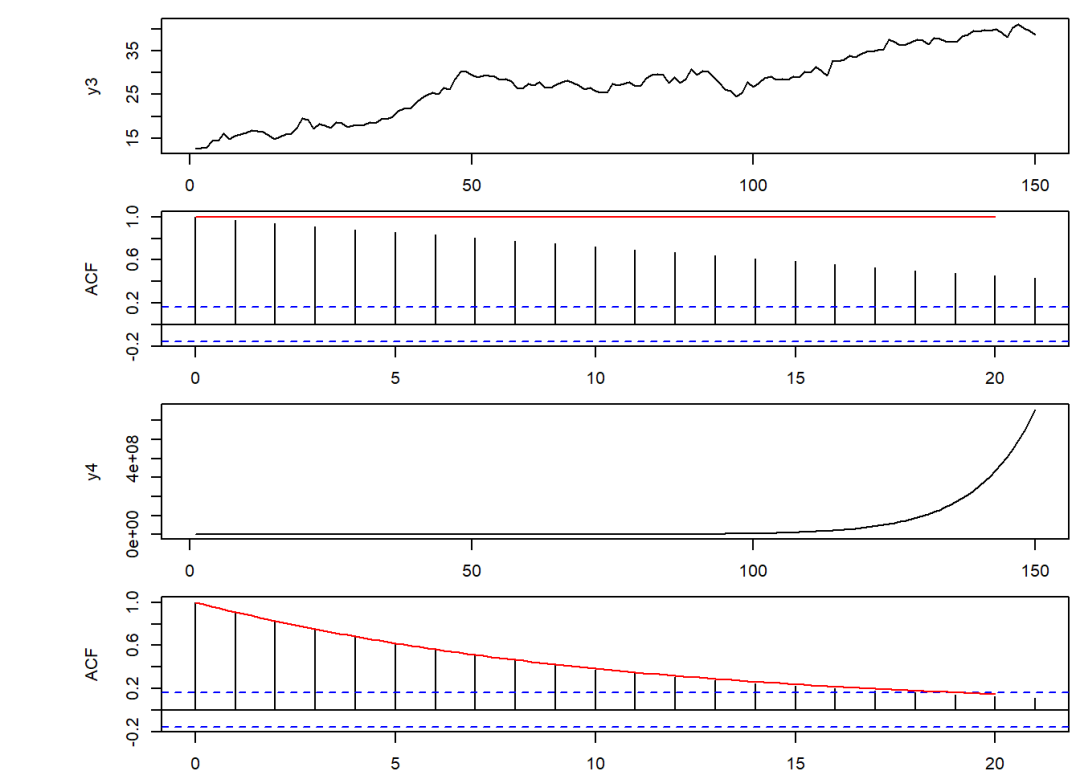
e2ea0696dd1e7c7670a1d448ee4b0f36.png

  • 当时，AR(1)过程就有明显的上升趋势，不再呈现类似时的震荡走势，这时的AR过程就是非平稳的；

  • 当时，AR(1)过程的走势由齐次解主导，呈现类似指数增长的非平稳过程；此时绘制出的自相关函数图象仍然是衰减的，这是由于acf()函数不会区分时间间隔的正负，绘制的实际是的衰减过程。

1.2 AR()过程

AR(2)过程的形式如下：

通过Yule-Walker方法，可以推导出它的自相关系数满足如下关系：

，其中

因此当时，序列满足AR(2)过程的齐次式。若使AR(2)是平稳过程，它的齐次解必须收敛于0，也就是说，最终也会呈现向0衰减的趋势。

可以证明，对于任意而言，当时，自相关系数构成的序列也会满足对应AR()过程的齐次式。同理，若AR()是平稳过程，那么自相关系数应当呈现向0衰减的趋势（不一定是直接衰减，也可能呈现震荡衰减）。

如下，分别构造平稳的AR(2)和AR(3)过程：

y5 = y6 = rep(0, 200)
for(i in c(4:200)){
  y5[i] = 0.2 + 0.5*y5[i-1] -0.06*y5[i-2]+ epsilon[i]
  y6[i] = 0.2 + 0.9*y6[i-1] - 0.26*y6[i-2] + 0.024*y6[i-3] + epsilon[i]
}
y5 = y5[51:200]
y6 = y6[51:200]

par(mfrow = c(4,1),
    plt = c(0.15,0.99,0.2,0.9))
plot(y5, type = "l")
acf(y5)
curve(0.2^x + 0.3^x, 0, 20, add = T, col = "red")

plot(y6, type = "l")
acf(y6)
curve(0.2^x + 0.3^x + 0.4^x,
      0, 20, add = T, col = "red")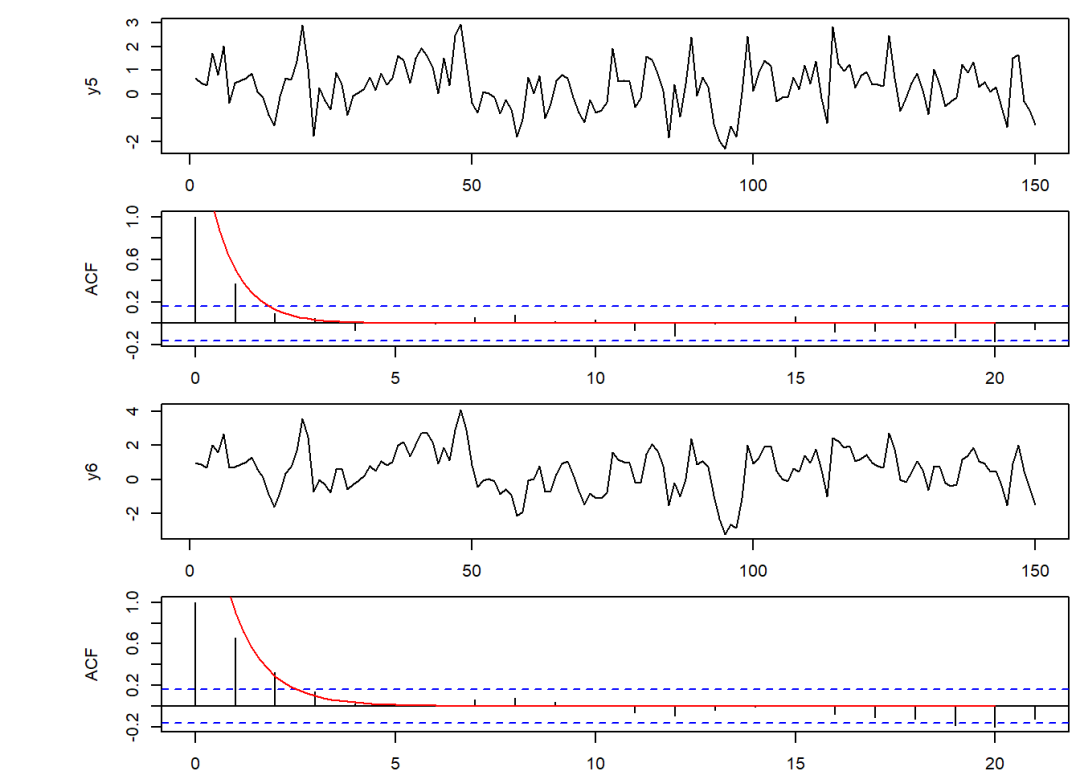
38d37fcc6e4fcbe9b968205ba5b25545.png

  • 从开始起，按照以特征方程的根为底数的指数函数相加进行衰减。

1.3 MA()过程

MA()过程的形式如下：

可以证明当时，。

也就是说，平稳MA()过程的自相关系数不是像AR()过程那样逐渐衰减至0的，而是在处及其之后直接降为0，这种分布形式称为截尾。

如下，分别构造MA(5)和MA(10)过程：

set.seed(123)
epsilon = rnorm(200)
y7 = y8 = rep(0,200)

for(i in c(11:200)){
  y7[i] = epsilon[i] + 1.9*epsilon[i-5]
  y8[i] = epsilon[i] + 1.9*epsilon[i-10]
}
y7 = y7[51:200]
y8 = y8[51:200]

par(mfrow = c(4,1),
    plt = c(0.15,0.99,0.2,0.9))
plot(y7, type = "l")
acf(y7)
points(5, 0.6, col = "red")

plot(y8, type = "l")
acf(y8)
points(10, 0.6, col = "red")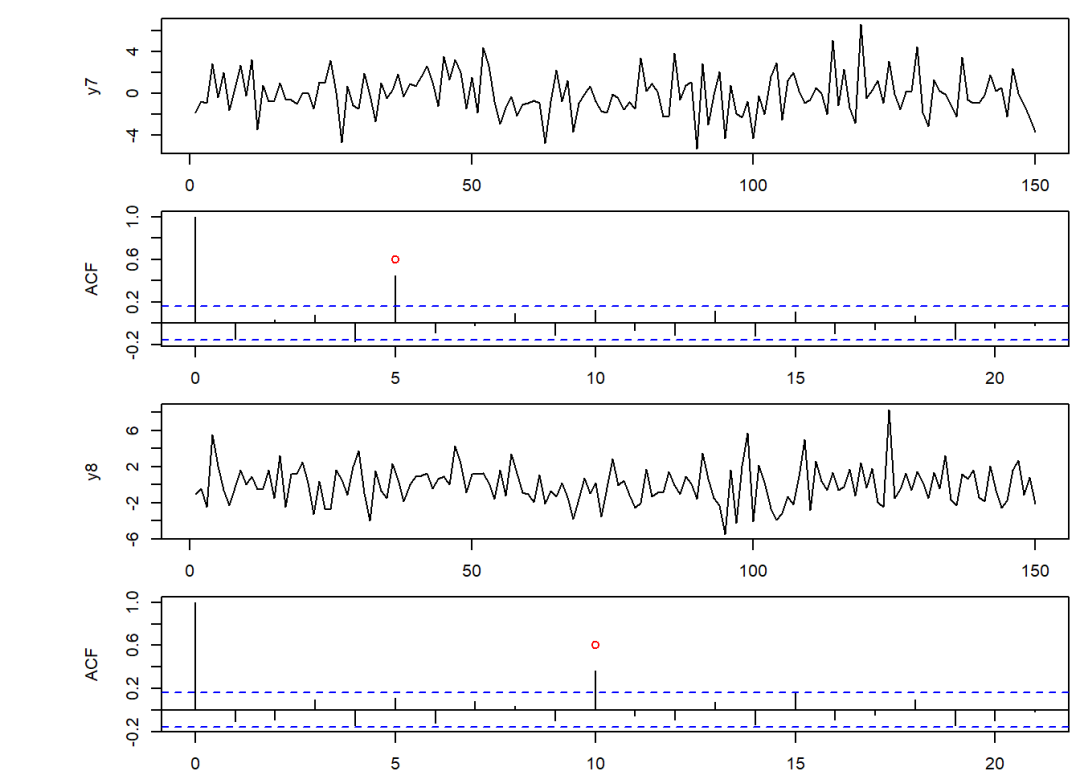
bc0bef8ed3700e3b3b8f986a658e4ed0.png

  • 为了效果明显，令，而取一个较大值；

  • 时，，而时也有可能不显著区别于0；

  • 当很小时，MA()退化为MA()，依次类推。因此对于MA过程，可以认为自相关函数截尾前的对应的值为其阶数。

1.4 ARMA(, )过程

同样通过Yule-Walker方法，可以得出当时，ARMA(, )过程的自相关系数满足如下关系：

上式与ARMA过程的齐次式等价，由于平稳ARMA过程的齐次解为0，因此从起，必定呈现衰减趋势（不一定是直接衰减，也可能呈现震荡衰减）。

如下，分别构造ARMA(5,5)和ARMA(5,10)过程：

set.seed(123)
epsilon = rnorm(200)
y9 = y10 = rep(0,200)

for(i in c(11:200)){
  y9[i] = 0.5*y9[i-5] + epsilon[i] + 1.9*epsilon[i-5]
  y10[i] = 0.5*y9[i-5] + epsilon[i] + 1.9*epsilon[i-10]
}
y9 = y9[51:200]
y10 = y10[51:200]

par(mfrow = c(4,1),
    plt = c(0.15,0.99,0.2,0.9))
plot(y9, type = "l")
acf(y9)
points(5, 0.8, col = "red")

plot(y10, type = "l")
acf(y10)
points(10, 0.8, col = "red")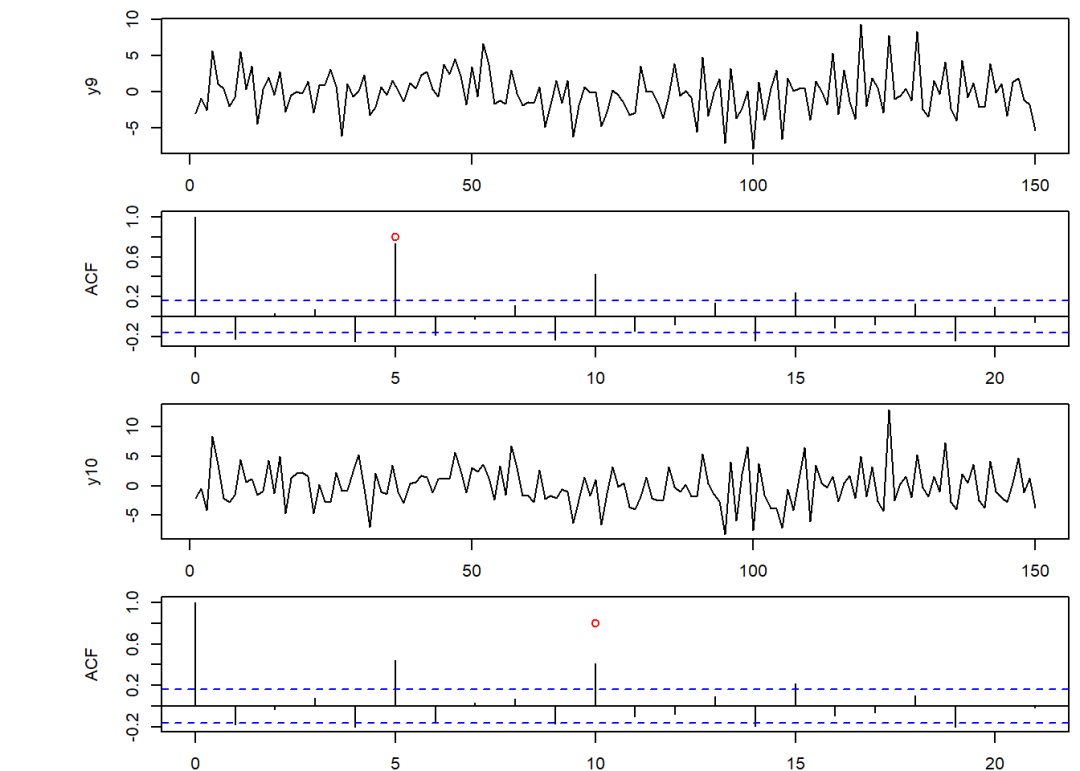
11d61e9882f02414fb318a80f2e9da82.png

  • 以上两个图象均是从起开始震荡衰减，并收敛于0。

1.5 总结

类型自相关函数特点
AR(1)绝对值沿指数函数直接衰减
AR()（可能震荡）向0衰减
MA()在处直接截尾于0
ARMA(, )从起（可能震荡）向0衰减

2 偏自相关函数

偏自相关系数（partial autocorrelation function, PACF）是排除与之间的、、...、的影响后的相关系数，记为，有。

记。利用如下回归方程可计算：

同理，利用如下回归方程可计算：

依次类推。

AR()过程本身就是一个自回归方程，当时，。也就是说，AR()过程的偏自相关系数构成的序列呈截尾分布。

在R中，可以设置acf()函数的参数type = partial，也可以直接使用pacf()函数绘制偏自相关函数。

pacf(x, lag.max, plot, na.action, ...)

：
：

par(mfrow = c(2,1),
    plt = c(0.15,0.99,0.15,0.9))
pacf(y1)
pacf(y6)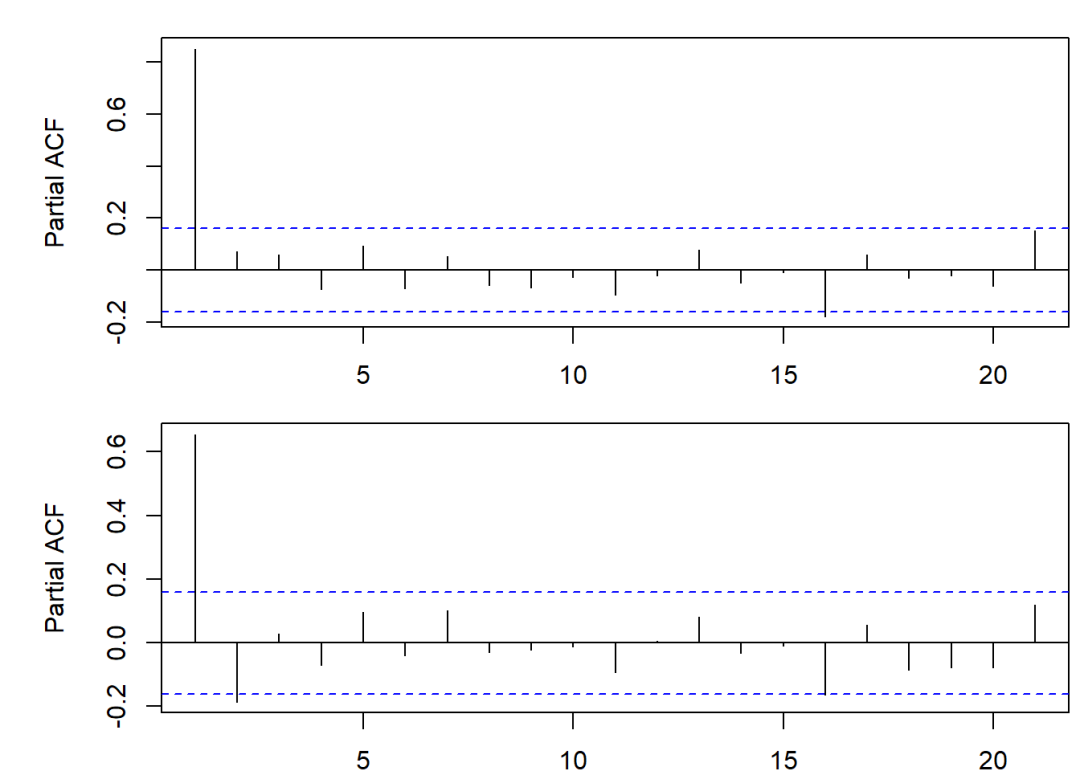
243738b888748dc476ee55f380fad83a.png

  • 对于，由于很小，因此也不显著区别于0。

对于MA()过程，偏自相关系数衰减于0。

对于ARMA(, )过程，从开始起，偏自相关系数逐渐衰减于0。

：
：

par(mfrow = c(2,1),
    plt = c(0.15,0.99,0.15,0.9))
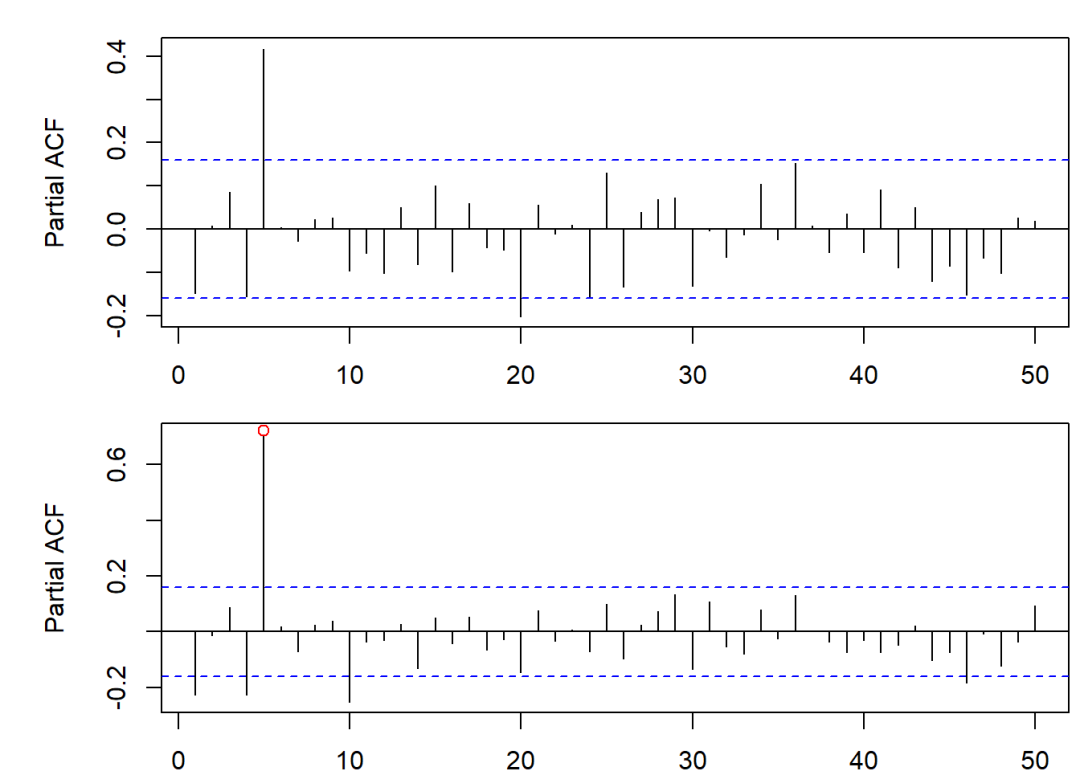
pacf(y7, lag.max = 50)
pacf(y9, lag.max = 50)
points(5, 0.72, col = "red")
ca728e73c7ac6fdfde6dfdd23351bba0.png