递归方程的求解（代入、递归树和主方法）

递归方程

递归方程之前提到过，就是部分算法在求解的过程中使用了将一个问题划分成几个等价的小问题，在这个过程中，我们就可以列出一个等式。
（如归并排序中，将一个大数组拆分成两个小数组分别计算，然后用O(n)的代价合并，
T(n) = T(n/2)+O(n)就是一个递归方程）

那么，在得到一个递归方程之后，我们应该如何求解问题呢？

替换法/代入法

我们都知道，归并排序的时间复杂度为O(nlogn)，那么我们以后看到和上面给出的归并排序差不多的递归方程时，我们可能心中就有了一些猜想。
没错，这个方式就是通过经验经行猜测
比如T(n) = 2T(n/2 + 17) + n，因为我们之前说过时间复杂度这个东西和常数项等关系不大，所以我们自然会将其和nlog进行联系，那么此时我们就需要带入，进行验证。

需要注意，在使用数学归纳法的时候，我们是可以舍弃前几项的
因为算法的时间复杂度并非严格的数学计算，我们可以忽略很多东西，而且在θ等标记符的定义过程中我们也强调了n0的含义。

但是，猜也是需要积累经验的，对一些奇怪的问题我们可能很难做到一次猜对，很自然，我们可以考虑先猜一个上下阶，然后不断逼近的方式。
那么我们就需要一些常见的时间复杂度的大小比较：
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³）……随后是指数，阶乘函数是最大的。
需要注意的问题：

• 任意底数的logn都要比多项式低阶
• 不同底数的log是同阶的，只相差一个系数（换底公式）

随后是一个蛮奇怪的问题，就是在计算下面的时间复杂度时，我们的做法可能有一点不同

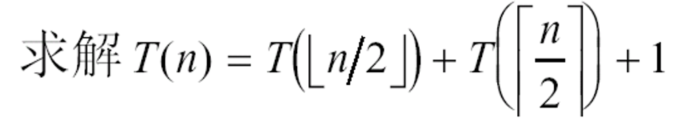
我们可以通过猜测的方式，达到O(n)的程度，但是当将O(n)带入时，会发现：

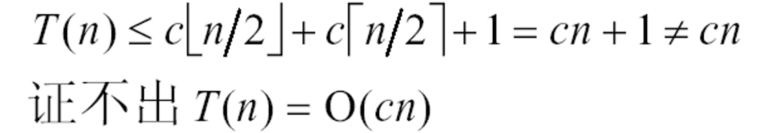
此时我们最可能的想法就是要计算O(nlogn)了，因为低阶的已经不能证明了。
但正好相反，我们的做法是在原来的基础上减去一个常数项

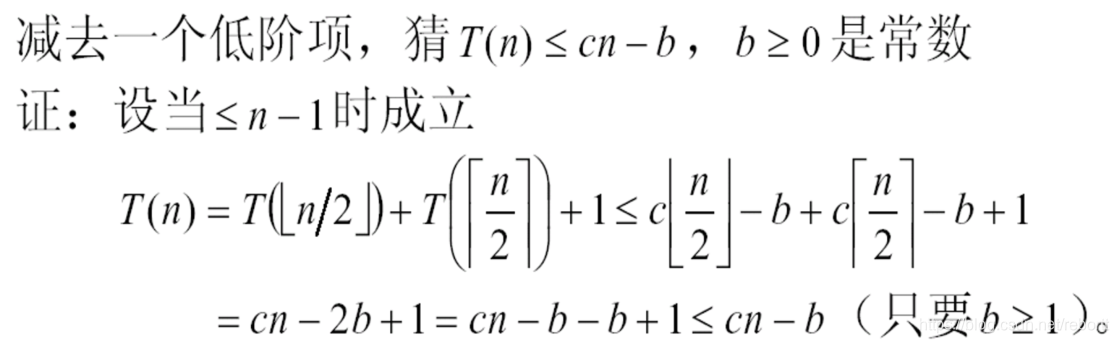
这是因为等式距离cn只差了一个常数项，而递归方程的左边只有一个T函数，而右边则有两个，那么在用右边的式子代替左边时，我们就可以减去双倍的常数项，就可以保证等式成立了。

等等，还有一种比较常见的变型：
有时我们会遇见一些奇形怪状的问题，比如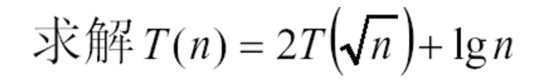
那么此时就要想一下是否能通过变脸替换来解决问题了。

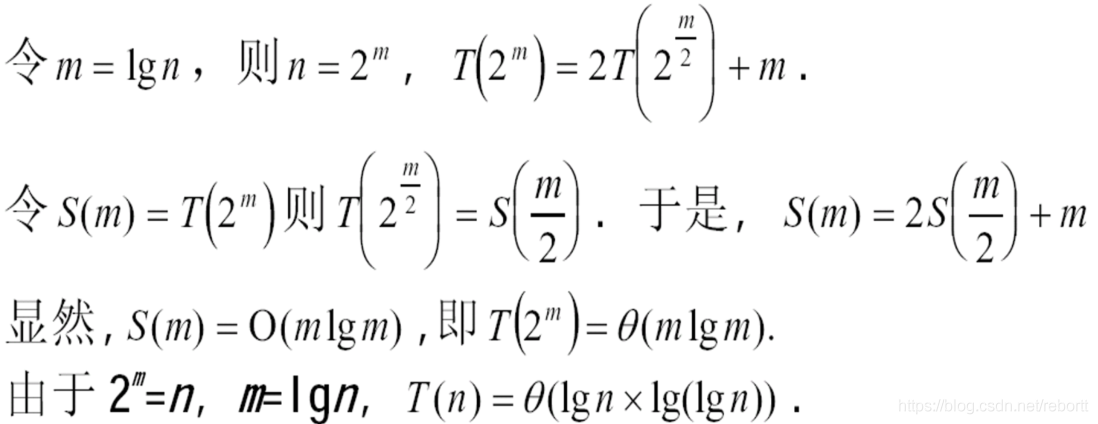
递归树法

这个方法是非常有趣的，也是最接近所有方法的本质的。

T(n) = 3T(n/4)+θ(n²)

我们可以这样想象，首先我们有一个大小为n的原问题，然后我们将他拆分成三个n/4大小的子问题，然后用了θ(n²)的代价。
将θ(n²)写在树根，那么这个根节点就应该有3个孩子节点，每一个孩子节点的大小是n/4

当我们将这个过程继续下去，直到最后一层，每一个结点的大小都是T(1)时
（ T(1)的代价我们默认为O(1) ），我们就可以说这棵树到了叶子节点。
因为每一层我们都将原规模缩小为原来的1/4，然后每一层的个数都是原来的三倍，所以最后一层的叶子节点个数应为3^log4n，
使用换底公式，我们可以得到最后一层的代价为θ(n^log43）。（以4为底3的对数）

而每一次的拆分，我们都将代价写在非叶子结点上，那么将代价相加，
再加上最后的叶子节点代价，我们就可以得到整体的代价了。
（说白了就是我把所有代价都写在结点上了，叶子节点就是T(1) == θ(1)，你把所有的加起来就行了）

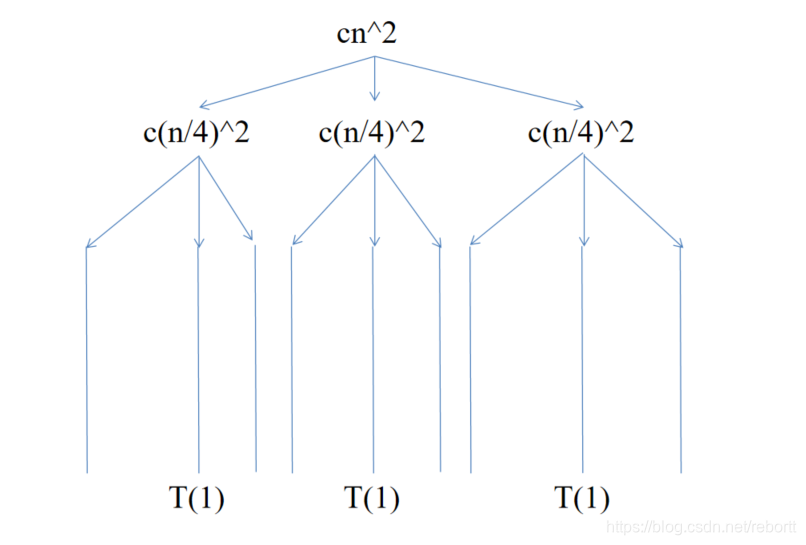
（学校ppt上的照片有水印，自己做的将就一下吧T_T）

在得到了每一层的代价之后，求和就是高数的事了。

主方法（最简单的方式）

好叭，可能很多人都和我一样，高数早就还给了老师，所以大佬们就给出了一个十分简单的方式来计算这类的时间复杂度。
这里给出主方法的一个分析方式，但不属于证明！
在我们计算递归树的时候，如果真的动手去算了上面的代价，那么会发现非叶子节点是一个等比数列，而叶子节点是另外一种不同的计算方式。在之前我们提到过，时间复杂度只考虑最高阶，所以我们只需要比较两者阶的高低，就可以得到时间复杂度了。

主方法通式：T(n) = aT(n/b)+f(n)

非叶子节点：θ( f(n) ) 不管ab怎么样，最后都是f(n)带一串的常数
叶子节点 ：同上面的递归树，n^logba（以b为底a的对数）
也就是比较两者的大小了。
声明：这里面的大小需要满足多项式的大于，也就是n和nlogn这样主方法是不成立的

1. 当f(n) > n^logba 时，有T(n)=θ( f(n) )
2. 当f(n) < n^logba 时，有T(n)=θ( n^logba )
3. 当f(n) = n^logba 时，有T(n)=θ( f(n)*logn )