现代通信原理6.1 常规调幅调制(AM)与抑制载波双边带(DSB-SC)调制
1、引言
考虑我们用麦克风采集语音信号,完成声-电转换,得到的电信号频率范围在20Hz~20kHz之间,显然属于低通信号。语音(电)信号为模拟随机信号,取值和时间上都是连续的,我们用 m ( t ) m(t) m(t)表示。图1中,我们用录音机获取了周杰伦新歌《说好不哭》大约24s的音频,左边图为波形,右边为频率。不难看出,主要频率集中在零频到7kHz之间。
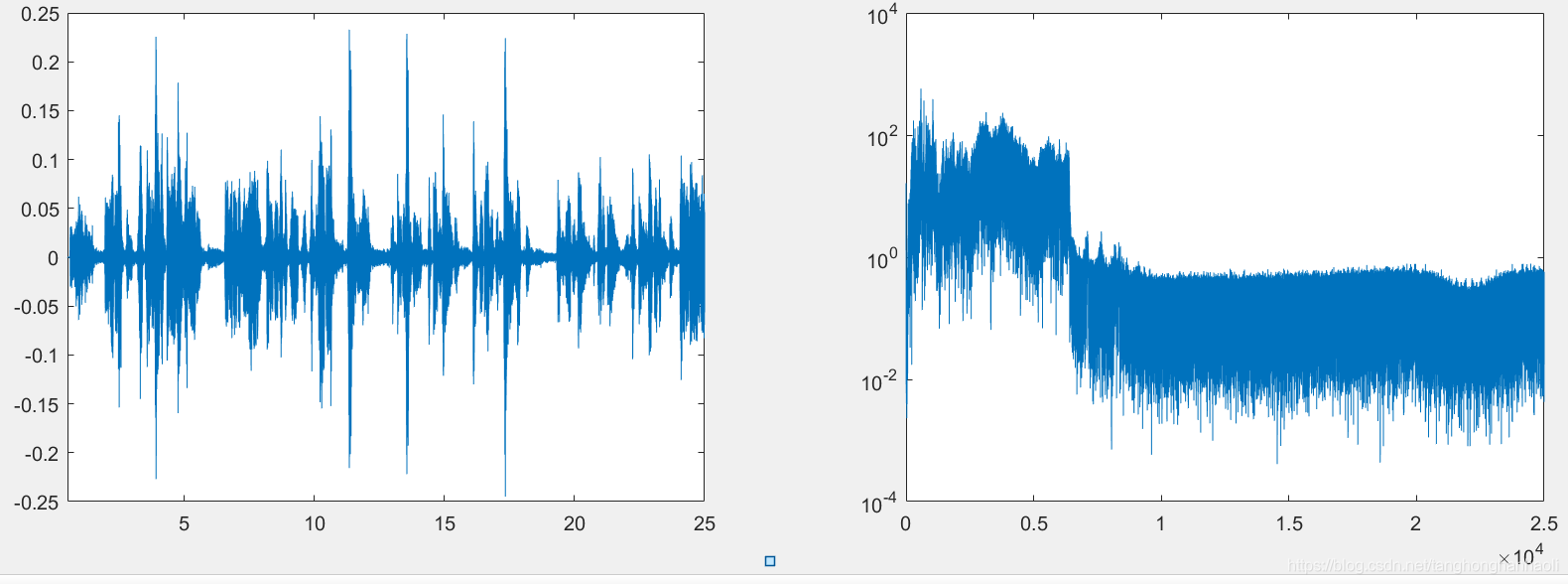
现在的问题是,如果我们想把类似图1中的这样的基带信号辐射到空间中,即采用无线方式进行传输,我们需要一定长度的天线。作为估算,一般来说我们认为天线长度需要等于无线电波长的
1
4
\frac{1}{4}
41(当然真正做天线设计时需要更准确的计算),这就意味着,如果我们的基带信号频率为3kHz,波长
λ
=
c
f
\lambda=\frac{c}{f}
λ=fc,这里的
f
=
3
f=3
f=3kHz为信号频率,
c
=
3
×
1
0
8
c=3\times 10^8
c=3×108m/s为光速,因此天线长度大约需要2.5km,显然这是不可能的。如果我们把信号频率提升到300MHz,则天线长度只需要0.25m。
我们还可能遇到这样一个问题。在无线传输中,由于所有无线信号都在空中叠加,因此会产生严重干扰,因此需要通过无线电管理,为不同系统分配不同带宽。以4G移动通信系统为例,包括1880-1900MHz、2320-2370MHz、2575-2635MHz等。这也意味着,我们需要将低通语音或者数字信号的频率升高,变为带通信号,才能够在分配的频段内传输。当然,在接收端需要将信号从带通再进行下搬移,变回低通信号。而这种低通变带通,带通变低通的过程,就称为信号的调制与解调。
这一讲,主要介绍模拟幅度调制,包括常规调幅调制(AM)、抑制载波双边带(SSB-SC)调制以及单边带(SSB)调制。
2、常规调幅调制(AM)调制器模型
AM调制器模型如图1(a)所示。显然有
s
A
M
(
t
)
=
A
c
[
1
+
m
(
t
)
]
cos
2
π
f
c
t
.
(1)
\tag{1} s_{\rm AM}(t)=A_c[1+m(t)]\cos 2\pi f_ct.
sAM(t)=Ac[1+m(t)]cos2πfct.(1)进一步,我们定义调幅指数
β
A
M
=
max
∣
m
(
t
)
∣
.
(2)
\tag{2} \beta_{\rm AM}=\max|m(t)|.
βAM=max∣m(t)∣.(2)
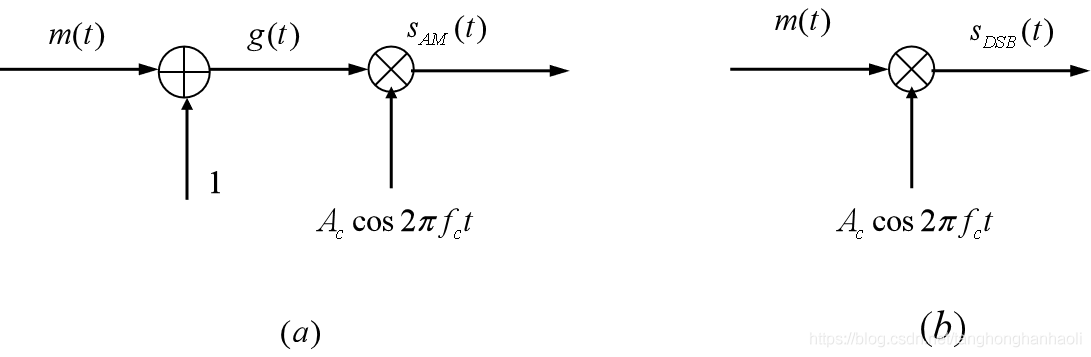
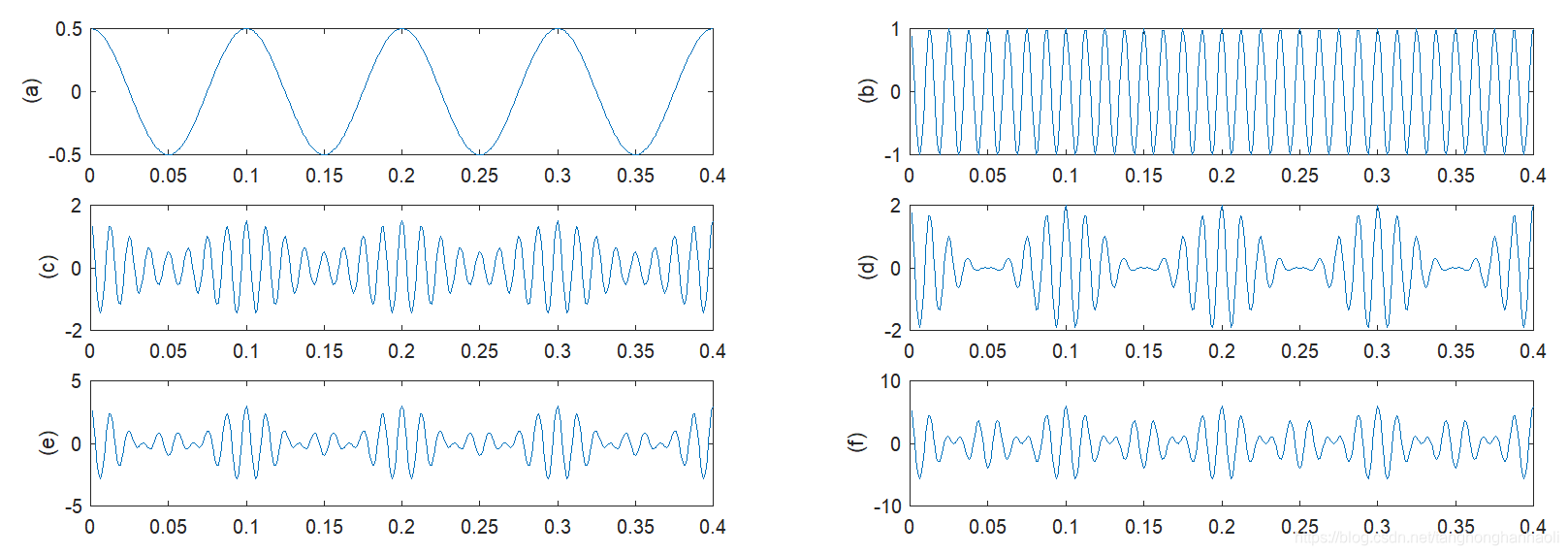
我们来看三种不同的调幅指数取值情况,即
β
A
M
<
1
\beta_{AM}<1
βAM<1、
β
A
M
=
1
\beta_{AM}=1
βAM=1以及
β
A
M
>
1
\beta_{AM}>1
βAM>1的情况,如图2所示,其中(a)、(b)分别为基带信号和载波信号波形;(c )、(d)、(e)、(f)中调幅指数
β
A
M
\beta_{AM}
βAM分别等于0.5、1、2和5。
事实上,AM调制的最大优点是接收机简单,可以采用包络检波法。这里我们不拟详述AM包络检波的详细过程,只在图3中给出示意,不难看出,二极管、电容和电阻即可构成包络检波器,通过电容充放电就可以跟随已调信号包络变化,而这里的包络,即(1)中的信号幅度 A c [ 1 + m ( t ) ] A_c[1+m(t)] Ac[1+m(t)]。
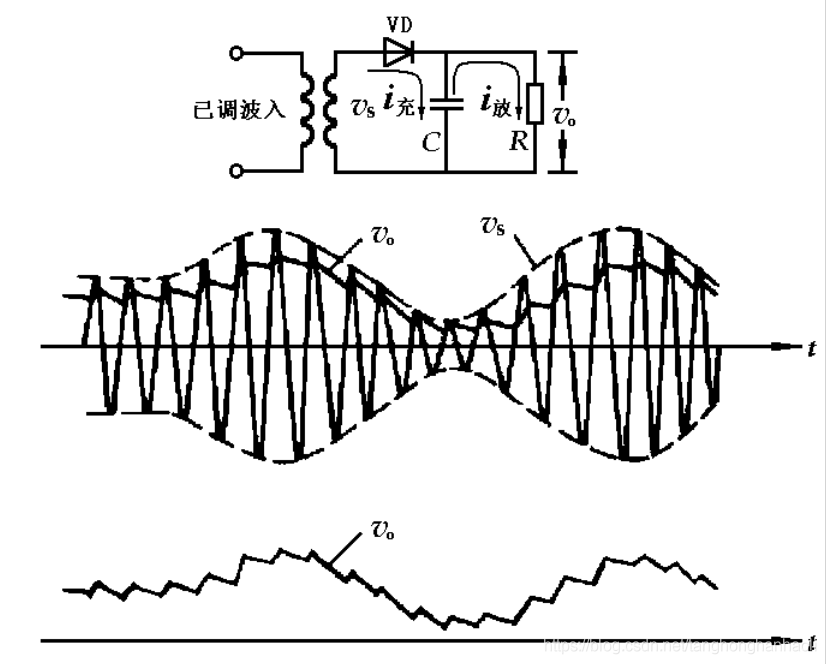
当AM信号的调幅指数 β A M > 1 \beta_{\rm AM}>1 βAM>1时,包络检波会发生错误,如图4所示。此时,由于 1 + m ( t ) 1+m(t) 1+m(t)可能小于零,导致包络检波输出 ∣ 1 + m ( t ) ∣ |1+m(t)| ∣1+m(t)∣与之不等,故无法正确恢复出 m ( t ) m(t) m(t)。
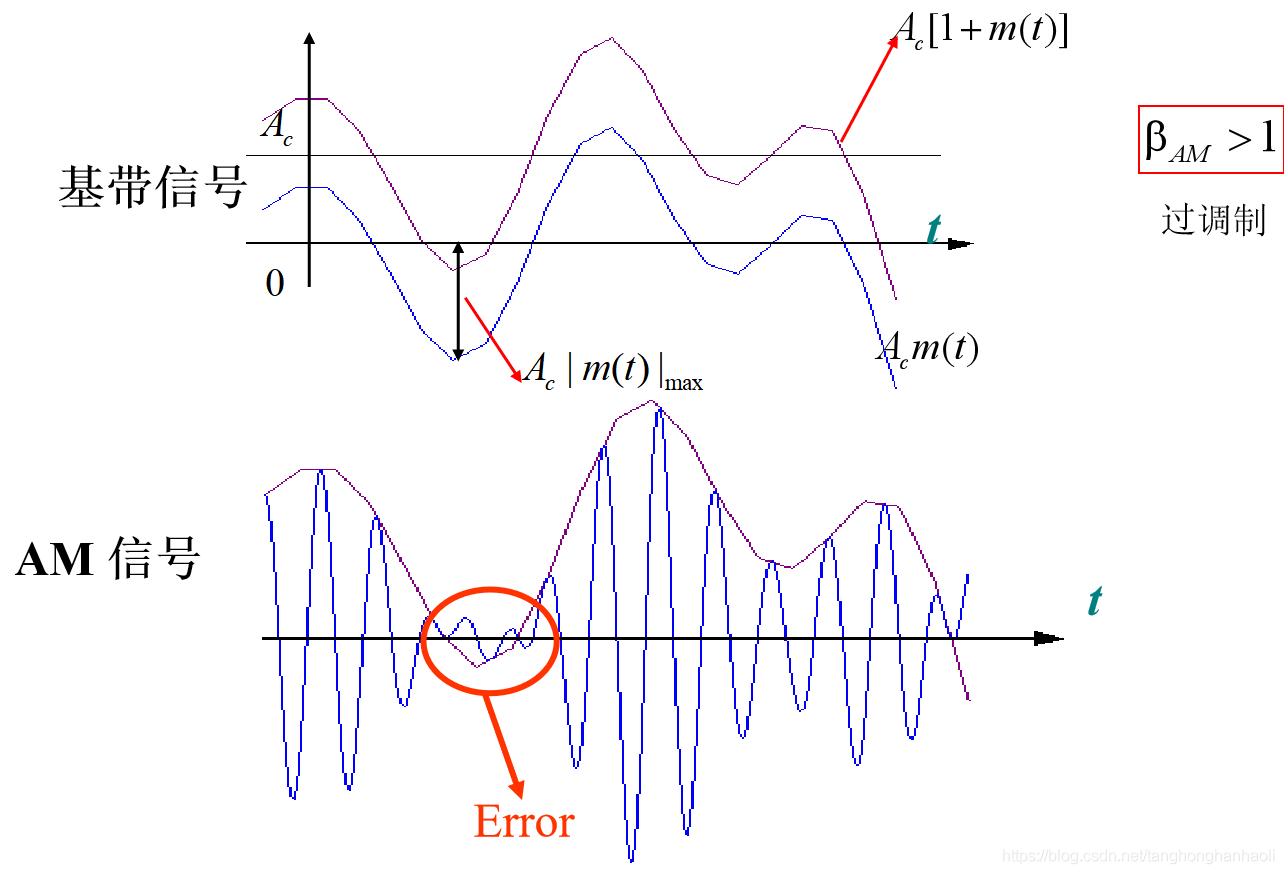
3、AM信号的傅立叶变换
根据(1),我们可以得到AM信号的频谱密度为
M
(
f
)
=
A
c
2
[
δ
(
f
−
f
c
)
+
δ
(
f
+
f
c
)
]
+
A
c
2
[
M
(
f
−
f
c
)
+
M
(
f
+
f
c
)
]
.
(3)
\tag{3} M(f)=\frac{A_c}{2}[\delta(f-f_c)+\delta(f+f_c)]+\frac{A_c}{2}[M(f-f_c)+M(f+f_c)].
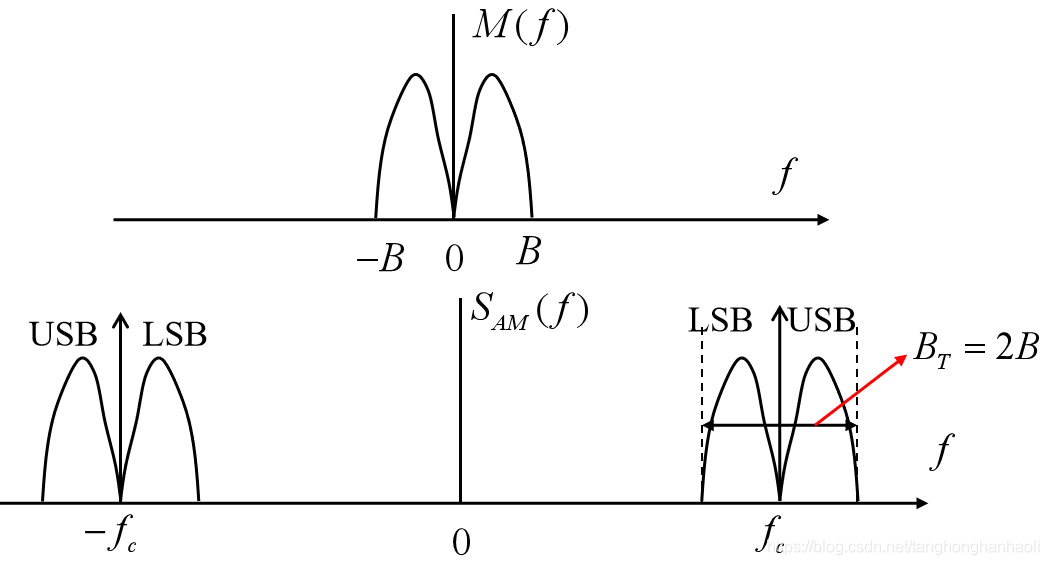
M(f)=2Ac[δ(f−fc)+δ(f+fc)]+2Ac[M(f−fc)+M(f+fc)].(3)其示意图如图5所示,这里
M
(
f
)
M(f)
M(f)为基带信号频谱,这里假定其最大频率(带宽)为
B
B
B,显然AM信号包含两个部分,一是离散载波,在
f
c
f_c
fc处的冲激;二是边带信号,包括上边带(大于
f
c
f_c
fc)和下边带(小于
f
c
f_c
fc)。由于包含上下两个边带,已调的AM信号带宽为2B,因此我们称AM为双边带信号。
4、AM信号功率与调制效率
下面我们来求AM信号的平均功率,有
s
A
M
2
(
t
)
‾
=
A
c
2
[
1
+
m
(
t
)
]
2
cos
2
2
π
f
c
t
‾
=
1
2
A
c
2
[
1
+
m
(
t
)
]
2
‾
+
1
2
A
c
2
[
1
+
m
(
t
)
]
2
cos
4
π
f
c
t
‾
,
(4)
\tag{4} \begin{aligned} \overline{s^2_{\rm AM}(t)}&=\overline{A_c^2[1+m(t)]^2\cos^2 2\pi f_ct}\\ &=\frac{1}{2}A_c^2\overline{[1+m(t)]^2}+\frac{1}{2}A_c^2\overline{[1+m(t)]^2\cos 4\pi f_ct},\\ \end{aligned}
sAM2(t)=Ac2[1+m(t)]2cos22πfct=21Ac2[1+m(t)]2+21Ac2[1+m(t)]2cos4πfct,(4)由于相对于
cos
4
π
f
c
t
\cos 4\pi f_ct
cos4πfct,
m
(
t
)
m(t)
m(t)的变化要缓慢得多,因此可以近似认为在
cos
4
π
f
c
t
\cos 4\pi f_ct
cos4πfct的一个周期之内,正负半周可以相互抵消,故上式中的第二项可以近似为0。进一步,我们有
s
A
M
2
(
t
)
‾
=
1
2
A
c
2
[
1
+
m
(
t
)
]
2
‾
=
1
2
A
c
2
+
1
2
A
c
2
m
2
(
t
)
‾
+
A
c
2
m
(
t
)
‾
,
(4)
\tag{4} \begin{aligned} \overline{s^2_{\rm AM}(t)}&=\frac{1}{2}A_c^2\overline{[1+m(t)]^2}\\ &=\frac{1}{2}A_c^2+\frac{1}{2}A_c^2\overline{m^2(t)}+A_c^2\overline{m(t)}, \end{aligned}
sAM2(t)=21Ac2[1+m(t)]2=21Ac2+21Ac2m2(t)+Ac2m(t),(4)我们一般假定
m
(
t
)
m(t)
m(t)为纯交流信号,即
m
(
t
)
‾
=
0
\overline{m(t)}=0
m(t)=0,因此有AM信号的平均功率为
P
A
M
=
P
c
+
P
m
=
1
2
A
c
2
+
1
2
A
c
2
m
2
(
t
)
‾
,
(4)
\tag{4} \begin{aligned} P_{\rm AM}&=P_c+P_m\\ &=\frac{1}{2}A_c^2+\frac{1}{2}A_c^2\overline{m^2(t)}, \end{aligned}
PAM=Pc+Pm=21Ac2+21Ac2m2(t),(4)这里,
P
c
=
1
2
A
c
2
P_c=\frac{1}{2}A_c^2
Pc=21Ac2以及
P
m
=
1
2
A
c
2
m
2
(
t
)
‾
P_m=\frac{1}{2}A_c^2\overline{m^2(t)}
Pm=21Ac2m2(t)分别称为载波功率和边带功率。显然,只有边带功率是用来传输基带信号
m
(
t
)
m(t)
m(t)的,据此,我们定义AM信号的调制效率为
η
A
M
=
P
m
P
c
+
P
m
=
1
2
A
c
2
m
2
(
t
)
‾
1
2
A
c
2
+
1
2
A
c
2
m
2
(
t
)
‾
=
m
2
(
t
)
‾
1
+
m
2
(
t
)
‾
.
(4)
\tag{4} \begin{aligned} \eta_{\rm AM}&=\frac{P_m}{P_c+P_m}=\frac{\frac{1}{2}A_c^2\overline{m^2(t)}}{\frac{1}{2}A_c^2+\frac{1}{2}A_c^2\overline{m^2(t)}}\\ &=\frac{\overline{m^2(t)}}{1+\overline{m^2(t)}}. \end{aligned}
ηAM=Pc+PmPm=21Ac2+21Ac2m2(t)21Ac2m2(t)=1+m2(t)m2(t).(4)
【思考题1】请问 m ( t ) m(t) m(t)为什么波形时调制效率最高?此时调制效率为多少?
【思考题2】如果 m ( t ) = a cos 2 π f m t m(t)=a\cos 2\pi f_mt m(t)=acos2πfmt为单音信号,则 a a a等于多少是可以得到最大的调制效率?此最大调制效率等于多少?
5、抑制载波双边带(DSB-SC)调制
抑制载波双边带调制(double sideband suppressed carrier, DSB-SC)调制器如图1(b)所示。显然,与AM不同之处在于,DSB-SC直接用
m
(
t
)
m(t)
m(t)进行调制,其已调信号的时域与频域表达式分别为
s
D
S
B
(
t
)
=
m
(
t
)
cos
2
π
f
c
t
,
S
D
S
B
(
f
)
=
A
c
2
[
M
(
f
−
f
c
)
+
M
(
f
+
f
c
)
]
.
\begin{aligned} s_{\rm DSB}(t)&=m(t)\cos 2\pi f_ct,\\ S_{\rm DSB}(f)&=\frac{A_c}{2}[M(f-f_c)+M(f+f_c)]. \end{aligned}
sDSB(t)SDSB(f)=m(t)cos2πfct,=2Ac[M(f−fc)+M(f+fc)].DSB-SC信号的傅立叶变换与AM相比,没有载频处的冲激,只有边带成分。显然,DSB-SC信号的平均功率为
P
D
S
B
=
1
2
A
c
2
m
2
(
t
)
‾
.
(4)
\tag{4} \begin{aligned} P_{\rm DSB}&=\frac{1}{2}A_c^2\overline{m^2(t)}. \end{aligned}
PDSB=21Ac2m2(t).(4)