fft 估计载波频率程序_毫米波雷达目标检测与参数估计算法(一)
牛喀学城车载77GHz毫米波雷达技术培训,欢迎致电或加微信:18917451722。
这一篇,我们主要学习下毫米波LFMCW雷达原理,下一篇,我们学习毫米波LFMCW雷达多目标配对与速度解模糊算法研究
1.1、引言
调频连续波雷达调制方式有多种,简单的如正弦波调制、三角波调制和锯齿波调制等,也有一些相对复杂的多种方式组合的调制方式[33H36]。经过多年的研宄与发展,目前常用的几种波形体制有三角波体制、锯齿波体制、频移键控()体制以及多频移键控(Multiple Frequency Shift Keying,MFSK)体制。不同的波形体制对应的信号处理方法也不同。三角波是由两个对称的线性调频连续波(Linear Frequency Modulated Continuous Wave,LFMCW)组成,分为上、下扫频,利用上、下扫频差拍信号频谱对称的性质,对距离和速度进行解耦,算法简单。锯齿波雷达由多个相同的线性调频连续波组成,通过二维快速傅里叶变换(Fast Fourier Transform,FFT)对距离和速度解耦合,算法复杂度高。三角波和锯齿波是目前毫米波车载雷达中常用的两种波形。频移键控连续波则由两个频率不同的恒频连续波组成,在单通道接收条件下,无法计算得到静止目标的距离。多频移键控雷达发射波形在频移键控连续波基础上,结合线性调频连续波的特点而产生,发射波形包含两个线性调制、互相交错上升的阶梯信号。该波形能够计算得到静止目标的距离,但由于利用到相位信息,在低信噪比情况下,距离精度不高。本章从基本的雷达方程着手,详细介绍这四种波形体制以及对应测距测速原理,并借助模糊函数工具着重对三角波和锯齿波雷达进行研宄及仿真。
1.2、雷达方程简介
连续波雷达通过发射天线向空间发射频率经过调制的电磁信号,信号在空间传播过程中遇到目标会反射回来,接收天线接收到目标反射回波,系统对目标反射回波进行相关的处理便可估计得到目标的距离、速度和方位角等参数,连续波雷达基本工作原理如图2-1所示:
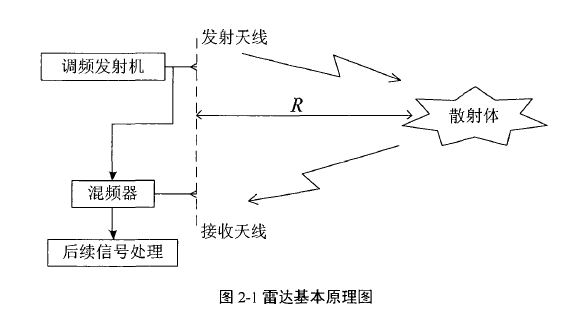
探测目标并确定其坐标是雷达最基本的任务,因此作用距离是雷达最重要的性能指标之一。作用距离决定了雷达能在多远的距离上发现目标,它的大小不仅取决于雷达本身的性能,包括发射机、接收系统、收发天线等分机参数,同时还和目标的性质及环境因素有关,如目标散射截面积(Radar Cross-Section,RCS)、天气状况等。雷达方程是描述雷达探测能力的主要理论工具,本章以点目标模型为例对雷达方程进行推导。假设雷达发射功率为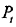 ,雷达发射天线增益为
,雷达发射天线增益为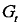 ,目标与雷达的距离为及,信号在自由空间均匀辐射,则在目标处的信号功率密度为:
,目标与雷达的距离为及,信号在自由空间均匀辐射,则在目标处的信号功率密度为:

发射信号遇到目标会被反射,反射信号功率的大小与功率密度和目标散射特性有关,用目标的散射截面积 ?来表征其散射特性。假设目标可以将接收到的信号功率无损的辐射出来,可得到目标散射功率为:
?来表征其散射特性。假设目标可以将接收到的信号功率无损的辐射出来,可得到目标散射功率为:

由式(2-6)可以看出,反射功率经过往返双倍的距离路程,所以接收到的目标回波功率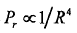 ,能量衰减非常大。雷达要能可靠地发现目标,必须满足接收的回波功率
,能量衰减非常大。雷达要能可靠地发现目标,必须满足接收的回波功率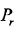 大于最小可检测信号功率
大于最小可检测信号功率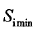 ,当
,当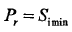 ,可得到雷达的最大作用距离:
,可得到雷达的最大作用距离:
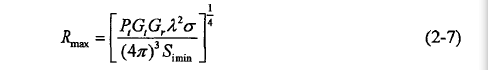
雷达方程给出了作用距离和各参数间的定量关系,但未考虑系统的实际损耗以及环境因素,而且方程中的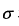 和
和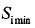 是两个不可准确预定的量,因此它常用来作为一个估算的公式,考察雷达各参数对作用距离的影响程度。
是两个不可准确预定的量,因此它常用来作为一个估算的公式,考察雷达各参数对作用距离的影响程度。
 2 月 21 日-23日,牛喀学城特邀来自德国海拉和奥迪公司的资深毫米波雷达专家刘博士深入介绍77G毫米波雷达的系统方案、软件架构、信号处理、硬件设计、波束形成、SAR成像、仿真测试标定、目标跟踪等开发和应用技术,以及第五代毫米波雷达的前沿技术,致力于帮助相关企业缩短市场投放时间,把握战略发展方向,帮助希望加入 ADAS 开发行业工程师提升职场竞争力。如您需要学习,可点击海报了解。
为响应防疫抗病毒号召,本课程支持线上远程学习,详情联系客服。
2 月 21 日-23日,牛喀学城特邀来自德国海拉和奥迪公司的资深毫米波雷达专家刘博士深入介绍77G毫米波雷达的系统方案、软件架构、信号处理、硬件设计、波束形成、SAR成像、仿真测试标定、目标跟踪等开发和应用技术,以及第五代毫米波雷达的前沿技术,致力于帮助相关企业缩短市场投放时间,把握战略发展方向,帮助希望加入 ADAS 开发行业工程师提升职场竞争力。如您需要学习,可点击海报了解。
为响应防疫抗病毒号召,本课程支持线上远程学习,详情联系客服。

1.3、三角波线性调频连续波
1.3.1、三角波测距测速原理
当雷达与目标存在相对运动时,传统的大时宽带宽线性调频连续波雷达存在距离与速度耦合的问题,造成目标距离估计产生误差。对称三角波雷达发射对称的上、下扫频段线性调频信号,对每一扫频段,通过将发射信号与接收信号进行混频获得回波差拍信号,差拍信号包含目标的距离和径向速度信息,利用上、下扫频段差拍信号频谱对称的性质,得到目标的距离和速度参数。对称三角波雷达发射信号、回波信号及差拍信号时频关系如图2-2所示:
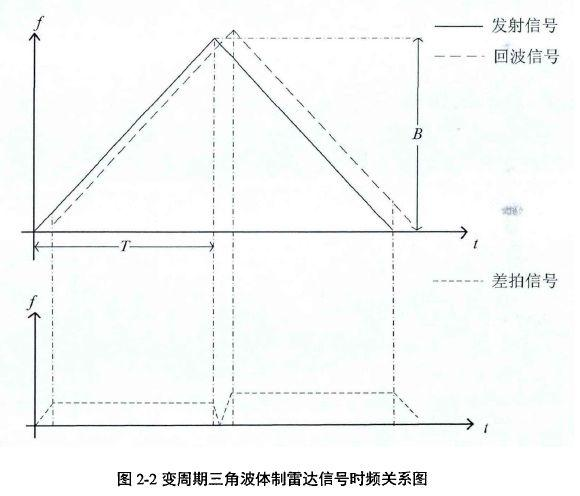
图2-2中,5和T分别为发射信号单个扫频段的扫频带宽和有效时宽。下面主要以上扫频段发射信号为例,分析差拍信号的表达式及其特性,提供目标参数估计的理论基础。三角波雷达上扫频段发射信号数学表达式为:

式(2_8)中,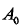 为发射信号幅度,
为发射信号幅度, 为载波中心频率,
为载波中心频率,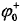 为上扫频发射信号初相,
为上扫频发射信号初相,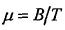 为扫频斜率。
为扫频斜率。
设在t=0时刻,雷达前方存在一个距离为r,以速度v(目标相对于雷达的径向速度,以接近雷达方向为正)匀速运动的目标,接收到的目标回波信号(忽略接收机噪声)数学表达式为:
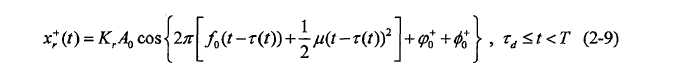
式(2-9)中,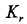 与目标散射截面积和传播衰减有关,
与目标散射截面积和传播衰减有关,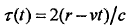 为t时刻目标与雷达间的距离引起的时延,c为电磁波在自由空间的传播速度,
为t时刻目标与雷达间的距离引起的时延,c为电磁波在自由空间的传播速度,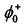 为信号反射产生的附加相移,
为信号反射产生的附加相移,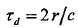 为目标初始距离对应的时延。将
为目标初始距离对应的时延。将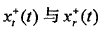 进行混频和低通滤波,得到差拍信号:
进行混频和低通滤波,得到差拍信号:


的线性调频信号的时宽带宽积。虽然D较大,但是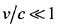 ,因此回波差拍信号是一个时宽带宽积很小的线性调频信号,可近似为一单频信号,数学表达式如下:
,因此回波差拍信号是一个时宽带宽积很小的线性调频信号,可近似为一单频信号,数学表达式如下:

由上、下扫频段回波差拍信号表达式可知,回波差拍信号中心频率均由两部分组成:一部分是由目标距离引起的信号时延产生的频率值 ;另一部分是由目标运动产生的多普勒频率值
;另一部分是由目标运动产生的多普勒频率值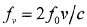 。通过谱估计方法(如FFT)估计得到上、下扫频段的回波差拍信号的频率,即可得到目标的距离和速度信息:
。通过谱估计方法(如FFT)估计得到上、下扫频段的回波差拍信号的频率,即可得到目标的距离和速度信息:
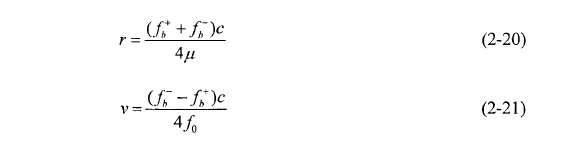
三角波雷达信号产生容易,对于单目标的情况,能够准确测出其速度与距离,但是对于多个运动目标的情况,简单的三角波雷达信号无法解决上、下扫频的多目标频率配对问题,存在多目标配对问题,容易出现虚假目标。
1.3.2、三角波模糊函数
模糊函数是雷达系统分析和综合的重要工具,它回答了发射什么样的波形、在采用最优信号处理的条件下系统具有什么样的分辨力、模糊度、测量精度和杂波抑制能力。三角波信号模糊函数在一些文献中都有详细介绍,为简化推导过程,本节采用复包络法进行单周期模糊函数推导。假设对称三角波LFMCM发射信号上扫频段时间为(-T,0],下扫频段时间为(0,T],发射信号数学表达式如下:
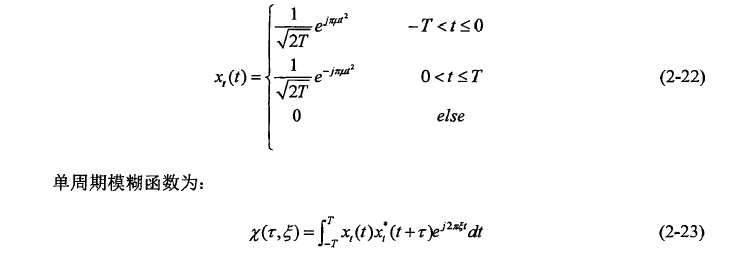
式(2-23)中,: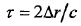 表示两个目标距离差
表示两个目标距离差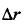 产生的时延,
产生的时延,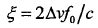 表示两个目标的多普勒频率差值。由于一般毫米波LFMCW雷达系统具有大时宽带宽积,必须考虑多普勒效应对复包络函数的影响,数学表达式如下:
表示两个目标的多普勒频率差值。由于一般毫米波LFMCW雷达系统具有大时宽带宽积,必须考虑多普勒效应对复包络函数的影响,数学表达式如下:

定义,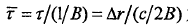 为归一化相对时延,代表两个目标的距离差占据的距离单元数;
为归一化相对时延,代表两个目标的距离差占据的距离单元数;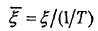 为归一化相对多普勒频率,代表T时间内相对多普勒频率振荡周期数;
为归一化相对多普勒频率,代表T时间内相对多普勒频率振荡周期数;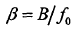 为相对带宽。将
为相对带宽。将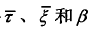 代入式(2-25),得到
代入式(2-25),得到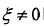 时的模糊函数为:
时的模糊函数为:

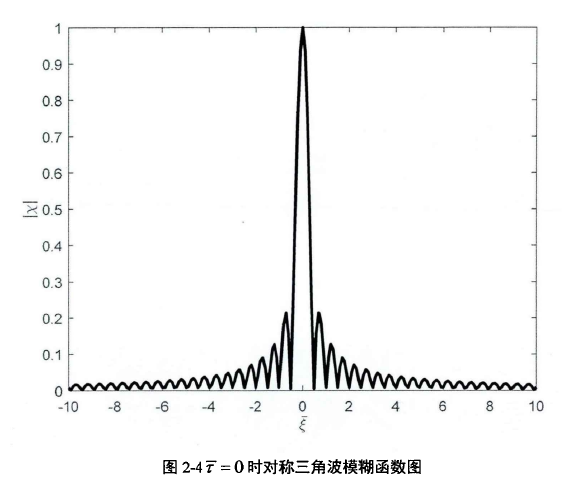
假设三角波雷达载波频率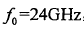 ,扫频带宽 B=200MHz,扫频周期T=lms,对称三角波单周期模糊函数如图2-3所示:
,扫频带宽 B=200MHz,扫频周期T=lms,对称三角波单周期模糊函数如图2-3所示:
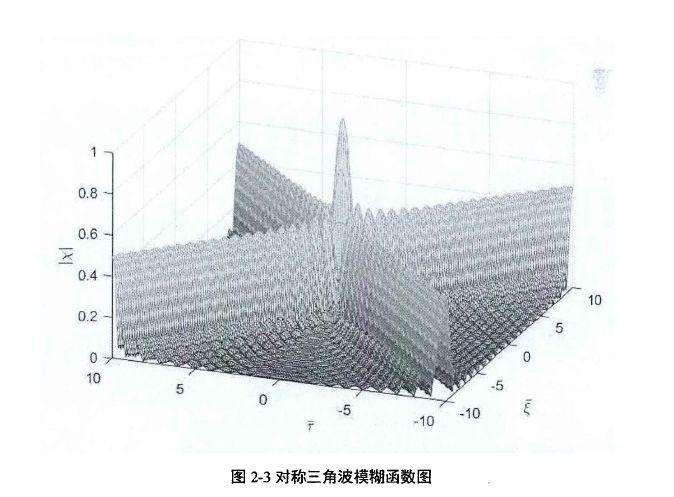
如图2-3所示,对称三角波模糊函数关于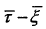 ,平面上原点
,平面上原点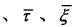 以及直线
以及直线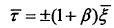 ,对称,能量主要分布在直线
,对称,能量主要分布在直线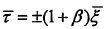 ,及其附近区域,且能量分布是连续的。
,及其附近区域,且能量分布是连续的。

同样,根据式(2-29)可得到归一化相对时延分辨率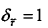 ,则距离分辨率为:
,则距离分辨率为:

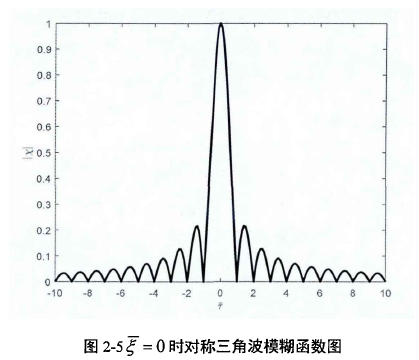
将模糊函数图沿时延轴进行切割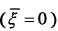 ,模糊函数波形如图2-5所示:
,模糊函数波形如图2-5所示:
1.3.3、仿真与分析
系统仿真参数如表2-1所示:

假设雷达前方存在一个目标,距离为50m,相对速度为20m/s,信噪比为10dB,对目标回波差拍信号进行1024点加窗FFT,仿真结果如图2-6所示:
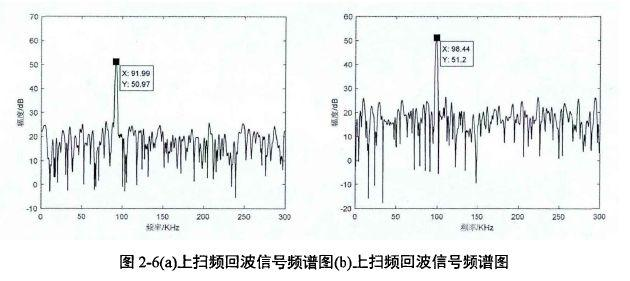
如图2-6所示,上、下扫频段目标回波差拍信号频谱中各出现一个峰值,频率分别为 ,根据式(2-20)和式(2-21)计算目标距离为49.98m,速度为20.16m/s。
,根据式(2-20)和式(2-21)计算目标距离为49.98m,速度为20.16m/s。
1.4、锯齿波线性调频连续波
1.41、锯齿波测距测速原理
锯齿波雷达也是利用差拍信号估计目标的距离和速度参数,但是由于是单扫频信号且存在距离和速度耦合的问题,不能像三角波线性调频连续波一样仅通过一维傅里叶变换得到目标的距离和速度。锯齿波LFMCW雷达发射信号时频图如图2-7所示:
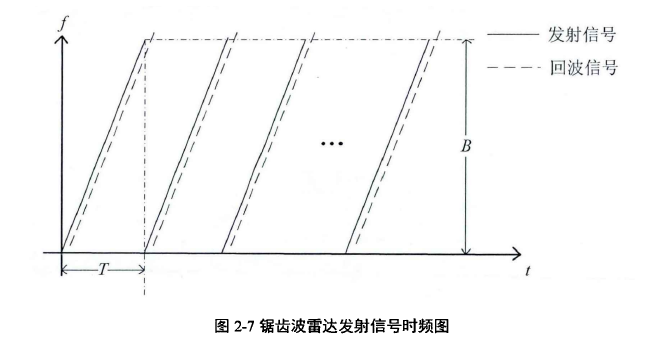
锯齿波雷达发射信号由多个单扫频段组成,周期重复,第个扫频周期锯齿波信号数学表达式如下:
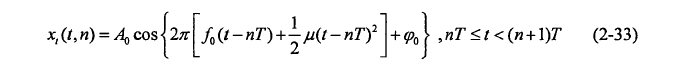
式(2-33)中,为一个相干处理周期内锯齿波的个数,其它参数意义与三角波中相同。假设在t=0时刻,雷达前方存在一个距离为r,以速度v(目标相对于雷达的径向速度,以接近雷达方向为正)匀速运动的目标,则接收到的目标回波信号为:
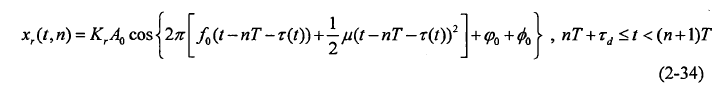
将 进行混频和低通滤波,得到差拍信号:
进行混频和低通滤波,得到差拍信号:


因为锯齿波线性调频连续波扫频周期T非常小,所以快时间维频谱峰值频率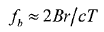 ,快时间维可以等效为距离维,频谱单元可以等效为距离单元。
,快时间维可以等效为距离维,频谱单元可以等效为距离单元。
仅仅通过单个扫频段的谱估计只能得到存在距离和速度耦合的差拍信号频率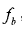 ,但在车载防撞雷达中,由于汽车的运动导致大部分目标都存在相对速度,而且相对速度可能较大,由相对速度产生的多普勒频移也会较大,所以通过/A去估计目标距离不能得到准确的距离信息。由式(2-39)可以看出,不同扫频段(慢时间维)的频谱峰值
,但在车载防撞雷达中,由于汽车的运动导致大部分目标都存在相对速度,而且相对速度可能较大,由相对速度产生的多普勒频移也会较大,所以通过/A去估计目标距离不能得到准确的距离信息。由式(2-39)可以看出,不同扫频段(慢时间维)的频谱峰值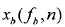 也是一单频信号,通过谱估计可以得到其频率
也是一单频信号,通过谱估计可以得到其频率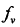 ,即目标的多普勒频移。根据
,即目标的多普勒频移。根据 即可得到目标的距离和速度信息:
即可得到目标的距离和速度信息:
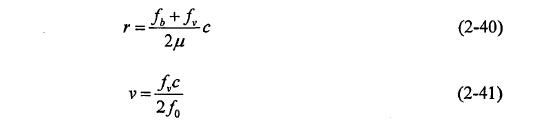
锯齿波体制雷达波形产生简单,相比三角波体制雷达,不存在多目标配对的问题,不会产生虚假目标,但系统信号处理算法比较复杂,导致硬件成本偏高。
1.4.2、锯齿波模糊函数
假设锯齿波雷达发射 个周期锯齿波,发射信号复包络S数学表达式为:
个周期锯齿波,发射信号复包络S数学表达式为:
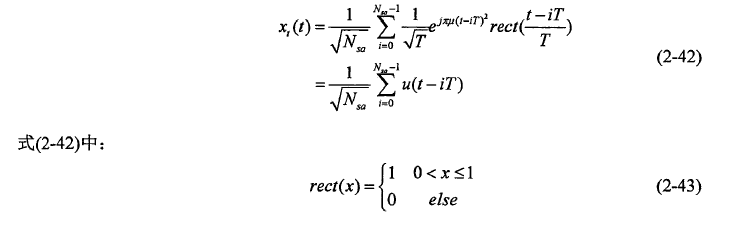
单个周期的锯齿波模糊函数与三角波上扫频段的模糊函数相同,可由式(2-25)和(2-26)直接得到,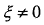 时的模糊函数为:
时的模糊函数为:


假设锯齿波雷达载波频率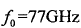 ,扫频带宽
,扫频带宽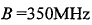 ,扫频周期
,扫频周期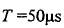 ,
,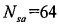 ,锯齿波模糊函数如图2-8所示:
,锯齿波模糊函数如图2-8所示:
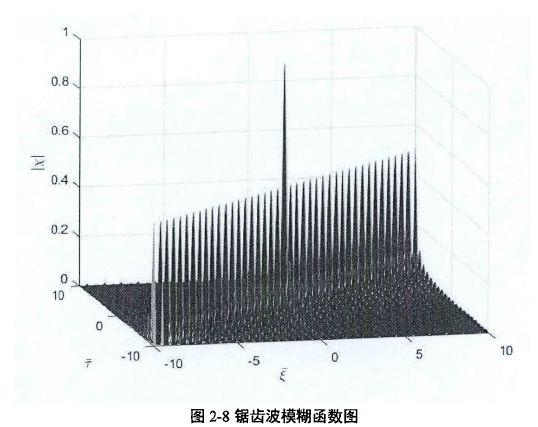
由式(2-50)可知,锅齿波信号模糊函数由单周期模糊函数被 加权后得到,加权因子决定了模糊函数在平面上的分布。由图2-8可知,与三角波不同,锯齿波模糊函数中心带能量主要分布在直线
加权后得到,加权因子决定了模糊函数在平面上的分布。由图2-8可知,与三角波不同,锯齿波模糊函数中心带能量主要分布在直线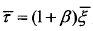 及其附近区域,且能量分布是离散的。
及其附近区域,且能量分布是离散的。

同样,根据式(2-50)可得到归一化相对时延分辨率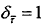 ,则距离分辨率为:
,则距离分辨率为:

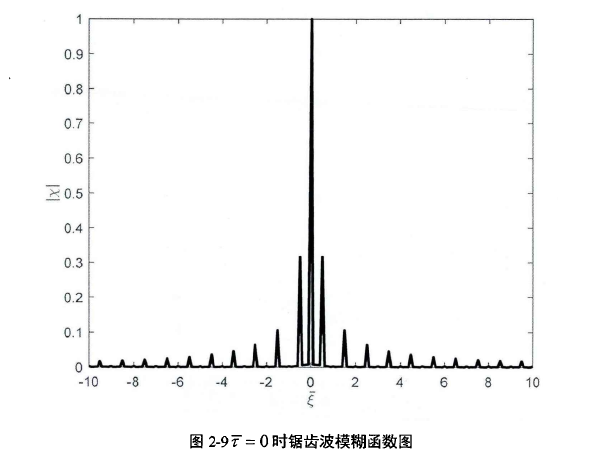
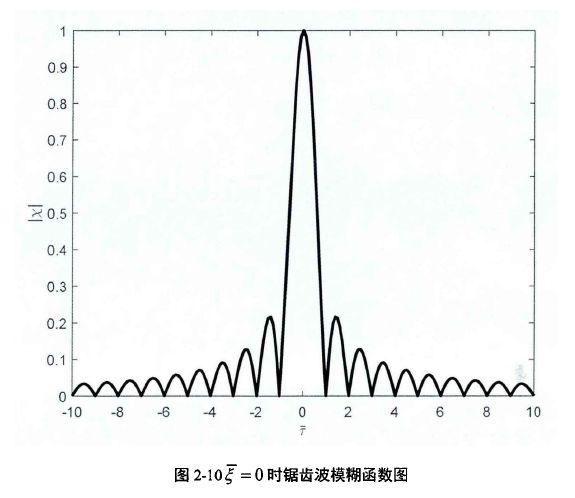
将模糊函数图沿时延轴进行切割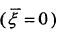 ,模糊函数波形如图2-10所示:
,模糊函数波形如图2-10所示:
1.4 仿真与分析
系统仿真参数如表2-2所示:
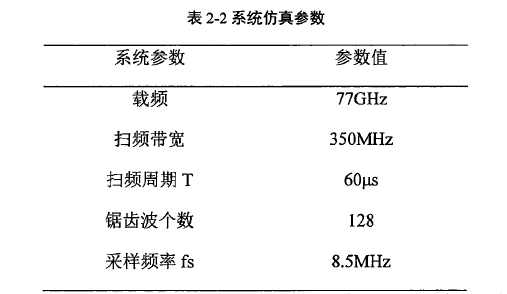
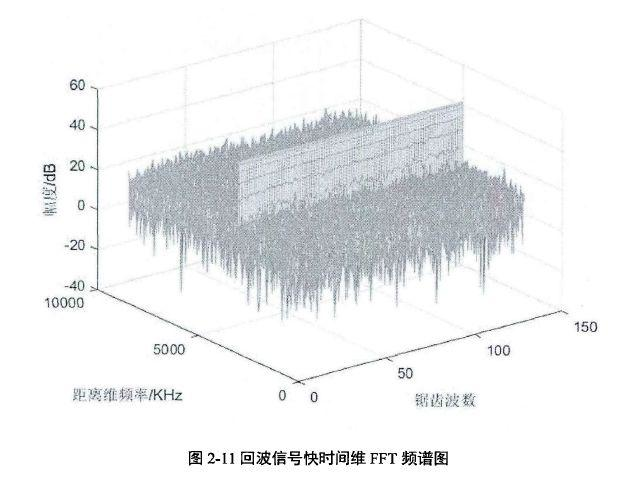
设雷达前方存在一个目标,距离为80m,相对速度为15m/s,信噪比为10dB,对目标回波差拍信号进行快时间维加窗FFT,仿真结果如图2-11所示。
单个扫频段的目标回波中频信号可以看作单频信号,对信号进行FFT,每个扫频段相同距离频谱单元均出现一个频谱峰值,在二维频谱上形成「山脊」状。对所有扫频段相同距离频谱单元的数据进行慢时间维加窗FFT,仿真结果如图2-12所示:
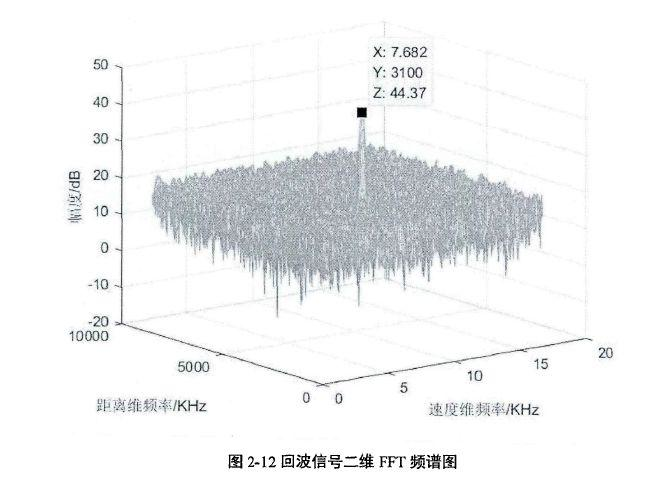
如图2-12所示,二维检测平面出现一个目标峰值,快时间维频谱峰值频率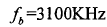 ,慢时间维频谱峰值频率
,慢时间维频谱峰值频率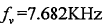 ,根据式(2-40)和(2-41)计算得到目标距离为79.91m,速度为14.96m/s。
,根据式(2-40)和(2-41)计算得到目标距离为79.91m,速度为14.96m/s。
1.5、频移键控连续波
频移键控体制雷达周期交替发送两个持续时间相同、中心频率不同的连续波。频移键控体制雷达发射信号频率与时间关系如图2-13所示:
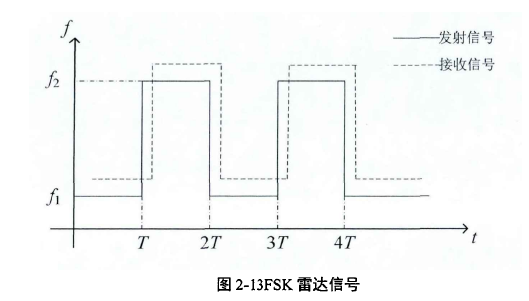

防撞雷达中,由于汽车的运动导致大部分目标都存在相对速度,因此可以根据差拍信号的频率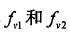 来计算目标的速度:
来计算目标的速度:

由于利用相位差计算目标距离,在低信噪比的情况下,距离估计精度会下降。
当前方有多个运动目标时,可以通过分析差拍信号的频谱将不同运动速度的目标区分开。因此,FSK体制雷达可区分多个不同运动速度的目标。当系统采用单通道接收时,对于相对静止的目标,由于信号幅度与目标反射系数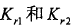 有关,无法获取准确的相位信息,因此无法检测静止目标。
有关,无法获取准确的相位信息,因此无法检测静止目标。
1.6、多频移键控连续波
多频移键控雷达发射波形在频移键控雷达波形基础上,结合LFMCW波形的特点而产生。发射波形包含两个频率线性调制、互相交错上升的阶梯信号,如图2-14所示:
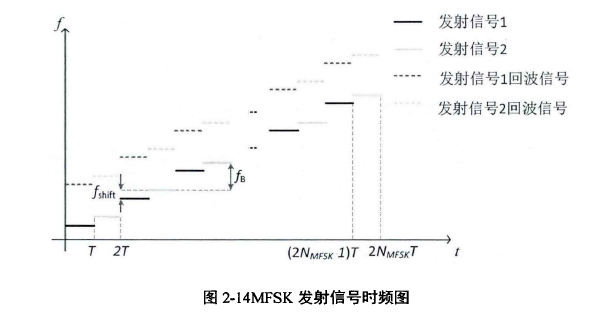
两个序列频率差值固定为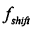 ,每次频率交替上升
,每次频率交替上升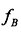 ,两个序列信号的数学表达式如下:
,两个序列信号的数学表达式如下:
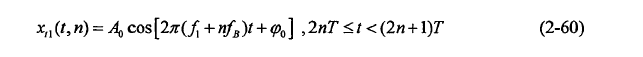



MFSK波形产生相对复杂,可同时检测多个目标并计算其距离和速度,并且不会产生虚假目标,但在低信噪比时,相位计算误差会导致距离和速度估计误差增大。
1.7、本章小结
本章主要介绍了目前常用的几种车载雷达信号波形及其测距测速原理。三角波线性调频连续波信号产生容易,算法简单,但是对于存在多个运动目标的情况,简单的周期三角波雷达信号无法解决上、下扫频的多目标配对问题,容易产生虚假目标。锯齿波体制雷达相比三角波体制雷达,不存在多目标配对的问题,也不会产生虚假目标,但是需要进行二维谱估计,系统信号处理算法比较复杂。FSK及MFSK在计算距离时都利用了相位差,在低信噪比时会增大距离和速度估计误差。

 全面升级:2020智能网联汽车技术培训计划火热预定中
全面升级:2020智能网联汽车技术培训计划火热预定中



| 二月精品课程 | |
| 2/21-2/23 | 77G毫米波雷达设计及第五代雷达前沿专题 |
| 2/29-3/1 | ACC和AEB功能安全设计与分析技术培训 |





【说明】由于线上内容更新,牛喀网小程序正在官方审核,部分课程连接不可用,请登录微信商城了解




