数字信号处理---离散时间信号与系统

一、离散时间序列

离散时间序列信号是一个有序的时间集合，因此离散时间信号也称为离散时间序列。

1.1 序列的表示

离散时间序列一般用集合、解析表达式和图形三种方式表示。

集合表示法： $x[n] = \begin{Bmatrix} x_{n}, & n\in Z \end{Bmatrix}$ ，Z表示整数集合。

例如，x[n] = {1,2,3,4,5；n = 0,1,2,3,4}，一般简单表示为 x[n] = {1,2,3,4,5}。

解析表达式：如 $x[n] = sin(\frac{\pi}{5}n),-\infty <n<\infty$ 。

图形表示法：

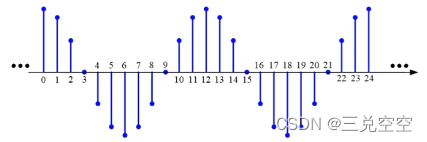
1.2 序列的分类

按序列长度分为有限长序列、无限长序列

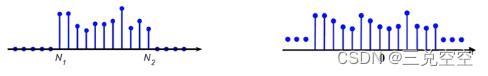
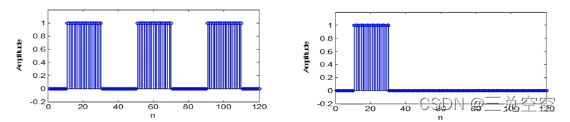
按序列周期性分为周期序列、非周期序列

按序列函数值分实数序列、复数序列
还可分为能量序列、功率序列

$E = \sum _{-\infty }^{\infty}\left | x[n] \right |^2 <\infty$ $P = \lim_{x->\infty}\frac{1}{2N+1}\sum _{n=-N }^{N}\left | x[n] \right |^2 <\infty$

1.3 常用时间序列

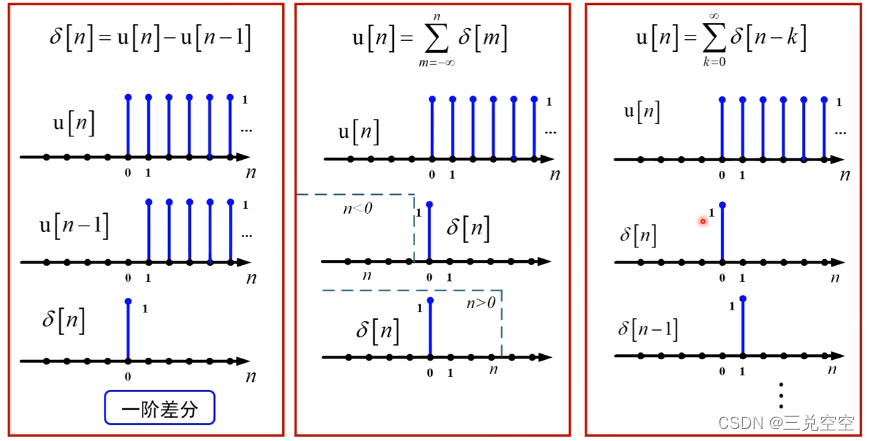
1.3.1 单位脉冲序列

$\delta[n] = \left\{\begin{matrix} 1 & n=0 \\ 0 & n\neq 0 \end{matrix}\right.$

$\delta[n] = \begin{Bmatrix} ..., & 0, & 1, & 0,& ... \end{Bmatrix}$

1.3.2 单位阶跃序列

$u[n] = \left\{\begin{matrix} 1 & n\geqslant 0 \\ 0 & n< 0 \end{matrix}\right.$

$u[n] = \begin{Bmatrix} ..., & 0, & 1, & 1,&1,&1,&1,& ... \end{Bmatrix}$

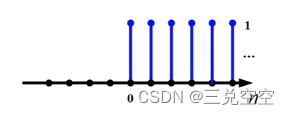
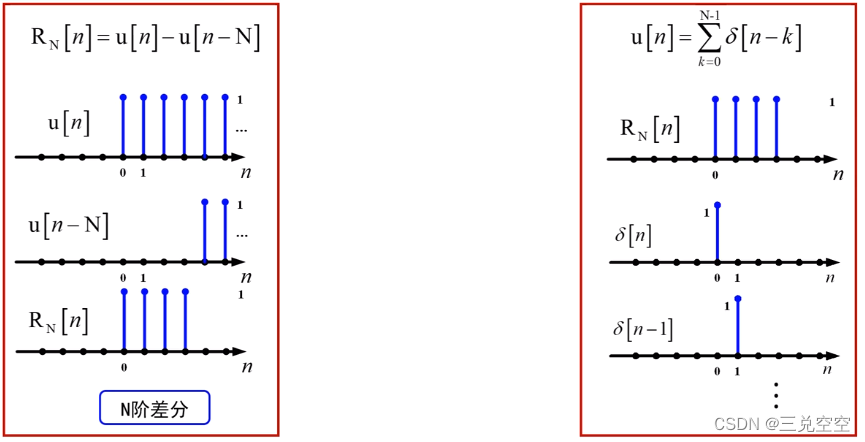
1.3.3 矩形序列

$R_{N}[n] = \left\{\begin{matrix} 1 &0\leqslant n\leqslant N -1 \\ 0& other \end{matrix}\right.$

$R_{N}[n] = \begin{Bmatrix} ..., & 0, & 1, & 1,&1,&1,&...1,&0,& ... \end{Bmatrix}$

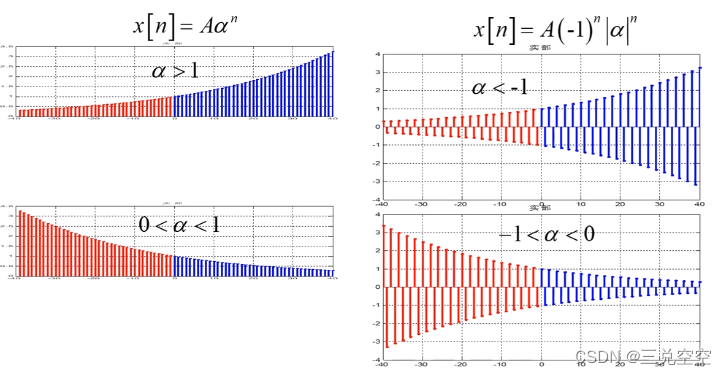
1.3.4 指数序列

$x[n] = A \alpha ^{n}$ 其中， $A,\alpha$ 为实数或者复数。

(1)实指数序列

若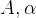 $A,\alpha$ 均为实数，x[n]称为实指数序列。

延伸

当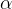 $\alpha$ 为负数时

$x[n] = A \alpha ^{n}$

可以表示为

$x[n] = A (-1)^{n} \alpha ^{n}$

由于

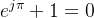
$e^{j\pi } +1 =0$

所以

$x[n] = A e^{jn\pi} |\alpha| ^{n}$

也可以表示为

$x[n] = A Cos(n\pi )|\alpha| ^{n}$

(2)复指数序列

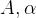若 $A,\alpha$ 均为复数，x[n]称为复指数序列。

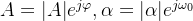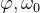令 $A=|A|e^{j\varphi },\alpha =|\alpha |e^{j\omega_{0}}$ ,其中 $\varphi,\omega_{0}$ 均为实数，则

$x[n]=A\alpha^n=|A|e^{j\varphi }(|\alpha|e^{j\omega_{0}})^n$

进一步

$x[n]=A\alpha^n=|A||\alpha|^ne^{j(\omega_{0}n+\varphi )}$

1.4 序列的分解

时域中，任意离散时间序列都能表示为某些基本序列及其延迟的加权和，最常用的基本序列为单位脉冲序列，任意离散时间序列 x[n] 都可由单位脉冲序列 $\delta [n]$ 表示：

$x[n]=\sum ^\infty _{-\infty }x[k]\delta[n-k]$

二、离散时间系统

离散时间系统的作用是将给定的输入序列通过一定的运算处理转变为输出序列。

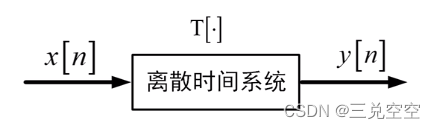
2.1 系统的表示

离散时间系统可由数学算子或变换 T[.] 表示，即系统的输出序列 y[n] 与系统输入序列 x[n] 之间的关系可表示为

y[n]=T[x[n]]

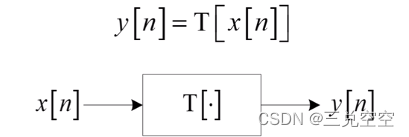
2.2 系统的分类

系统的主要属性包括：记忆性、线性、时不变性、因果性和稳定性。据此可以将系统分为：有记忆系统与无记忆系统、线性系统与非线性系统、时变系统与时不变系统、因果系统与非因果系统、稳定系统与非稳定系统等，其中最重要的是线性时不变系统。

1. 无记忆系统

系统的输出只与当前时刻输入相关

2. 线性系统

满足叠加原理的系统称为线性系统。

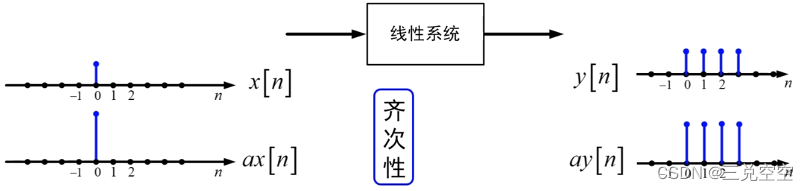
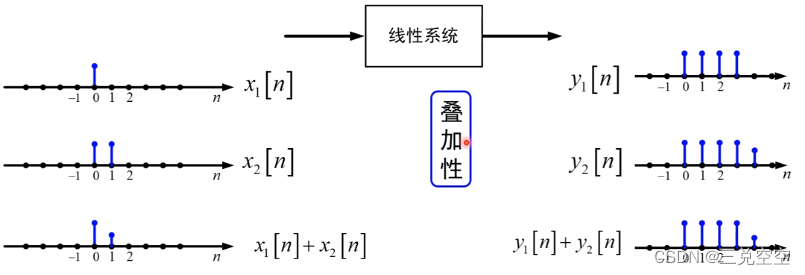
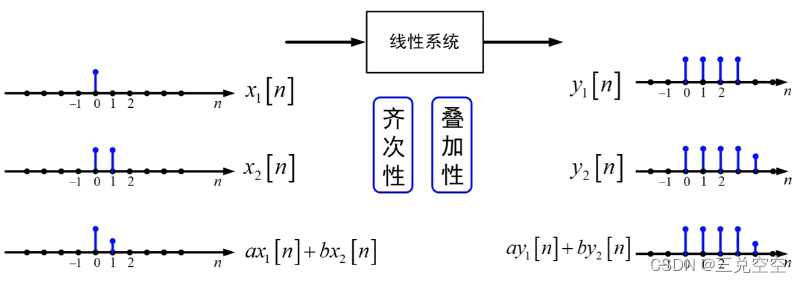
例1：

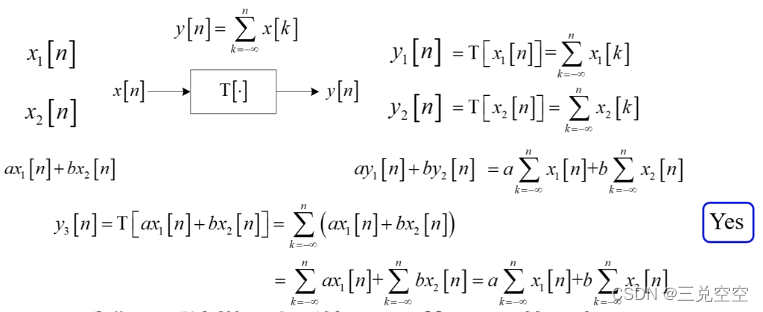
例2：

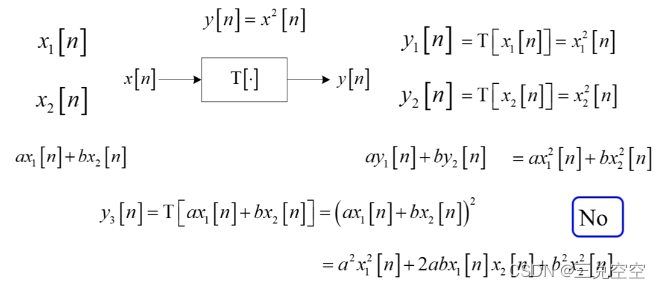
例3：

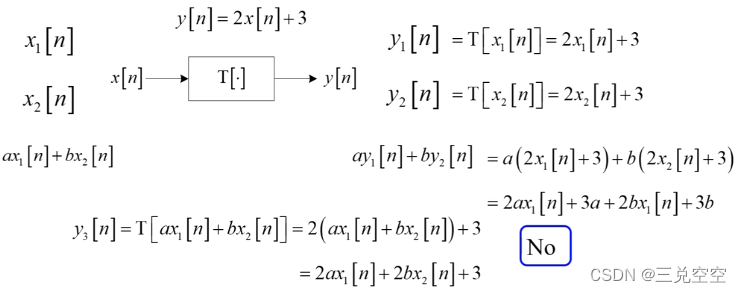
3. 时不变系统

系统的性能不随时间的改变而改变

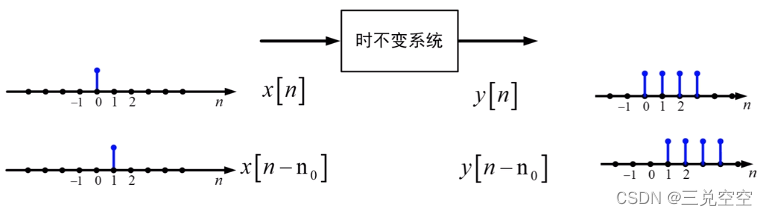
例1：

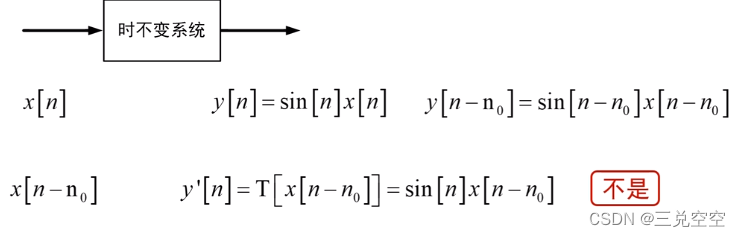
例2：

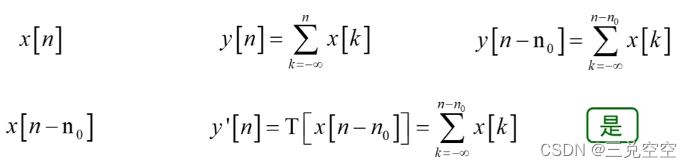
4. 因果系统

当前时刻输出仅取决于当前及以前时刻输入，而与以后的输入无关。

5. 稳定系统

有界输入产生有界输出，则系统稳定

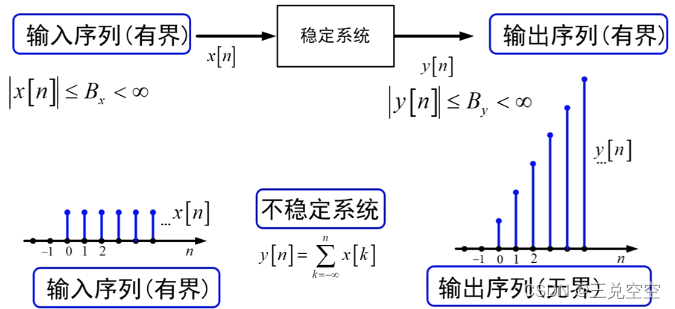
2.3 LTI系统卷积表示

任意序列均可以分解为不同延迟单位脉冲的线性组合

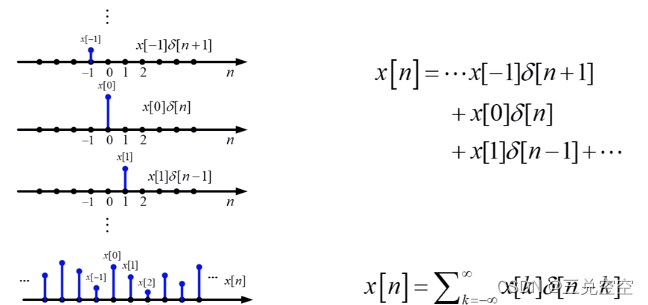
冲击响应的时不变性

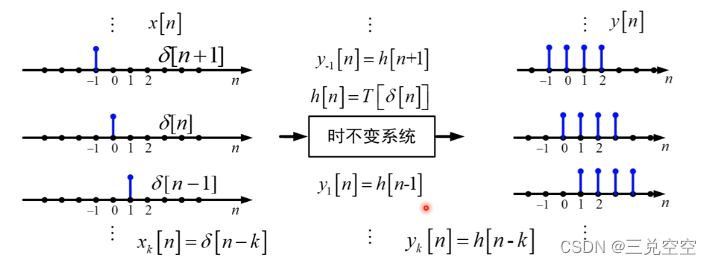
齐次时不变性

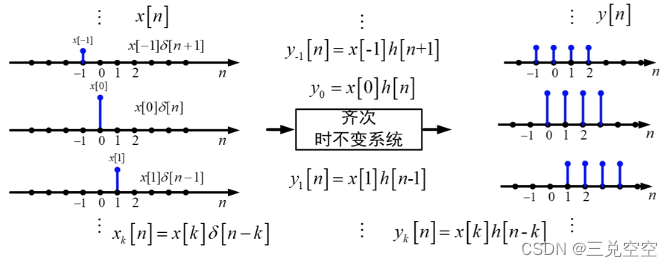
线性时不变性

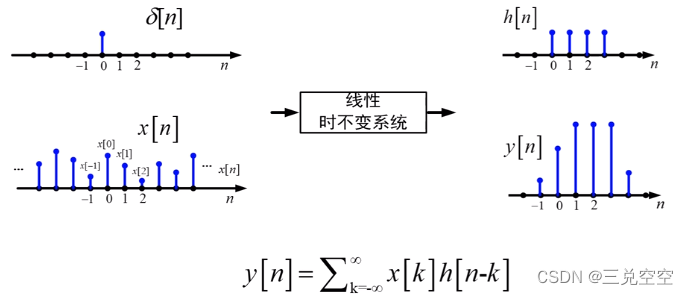
$y[n]=\sum ^\infty _{k=-^\infty}x[k]h[n-k]=x[n]*h[n]$

2.4 LTI系统的性质

2.5 线性常系数差分方程

三、小结