codeforces1312 D. Count the Arrays(推导 + 组合数)
D. Count the Arrays
time limit per test
2 seconds
memory limit per test
512 megabytes
input
standard input
output
standard output
Your task is to calculate the number of arrays such that:
- each array contains nn elements;
- each element is an integer from 11 to mm;
- for each array, there is exactly one pair of equal elements;
- for each array aa, there exists an index ii such that the array is strictly ascending before the ii-th element and strictly descendingafter it (formally, it means that aj<aj+1aj<aj+1, if j<ij<i, and aj>aj+1aj>aj+1, if j≥ij≥i).
Input
The first line contains two integers nn and mm (2≤n≤m≤2⋅1052≤n≤m≤2⋅105).
Output
Print one integer — the number of arrays that meet all of the aforementioned conditions, taken modulo 998244353998244353.
Examples
input
Copy
3 4output
Copy
6input
Copy
3 5output
Copy
10input
Copy
42 1337output
Copy
806066790input
Copy
100000 200000output
Copy
707899035Note
The arrays in the first example are:
- [1,2,1][1,2,1];
- [1,3,1][1,3,1];
- [1,4,1][1,4,1];
- [2,3,2][2,3,2];
- [2,4,2][2,4,2];
- [3,4,3][3,4,3].
题意:
给定n, m,在1 ~ m 中取 n 个元素,有且只有两个元素相同,将它们排成在最大值左侧严格单增,在最大值右侧严格单减的序列。问这样的序列有多少个?答案对998244353取模
思路:
先选择n - 1个数排成递增序列,有 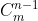 种
种
然后从这n - 1个数中选择一个除最大值以外的元素,新加一个到最后,有 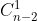 种
种
除去两个相同元素和最大元素,其余 n - 3 个元素选择若干个降序放到最大值后面,有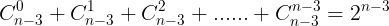 种
种
注意 n = 2 时答案为0,减少无谓的运算
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int mod = 998244353;
const int N = 1e5 + 10;
ll n, m;
ll inv(ll a)
{
return a == 1 ? 1 : (ll)(mod - mod / a) * inv(mod % a) % mod;
}
ll comb(ll n, ll m)
{
if(m < 0 || n< m)
return 0;
if(m > n - m)
m = n - m;
ll up = 1, down = 1;
for(ll i = 0; i < m; ++i)
{
up = up * (n - i) % mod;
down = down * (i + 1) % mod;
}
return up * inv(down) % mod;
}
ll qpow(ll a, ll b)
{
ll ans = 1;
a %= mod;
while(b)
{
if(b & 1)
{
ans = (ans * a) % mod;
}
a = (a * a) % mod;
b >>= 1;
}
return ans % mod;
}
int main()
{
while(~scanf("%lld%lld", &n, &m))
{
if(n == 2)
{
cout<<0<<'\n';
continue;
}
ll a = comb(m, n - 1);
ll b = (n - 2) % mod;
ll c = qpow(2, n - 3);
ll ans = (((a * b) % mod) * c) % mod;
cout<<ans<<'\n';
}
return 0;
}