用矩阵快速幂计算斐波那契数列
背景介绍
递推式和矩阵乘法
斐波那契数列有递推公式
F
n
+
2
=
F
n
+
1
+
F
n
n
∈
N
F_{n+2}=F_{n+1}+F_{n} \enspace n \in \mathbb{N}
Fn+2=Fn+1+Fnn∈N
我们可以把这个计算过程抽象成一个矩阵运算的过程。
[
F
n
+
2
F
n
+
1
]
=
[
1
1
1
0
]
⋅
[
F
n
+
1
F
n
]
\begin{bmatrix} F_{n+2}\\ F_{n+1} \end{bmatrix} = \begin{bmatrix} 1\enspace 1\\ 1\enspace 0 \end{bmatrix} \cdot \begin{bmatrix} F_{n+1}\\ F_{n} \end{bmatrix}
[Fn+2Fn+1]=[1110]⋅[Fn+1Fn]
那么对于第
n
n
n项,我们有:
[
F
n
F
n
−
1
]
=
[
1
1
1
0
]
n
−
1
⋅
[
F
1
F
0
]
\begin{bmatrix} F_{n}\\ F_{n-1} \end{bmatrix} = \begin{bmatrix} 1\enspace 1\\ 1\enspace 0 \end{bmatrix}^{n-1} \cdot \begin{bmatrix} F_{1}\\ F_{0} \end{bmatrix}
[FnFn−1]=[1110]n−1⋅[F1F0]
快速幂
对于一个指数为正整数的幂运算,我们有:
X
T
=
(
X
2
)
T
2
T
∈
2
,
4
,
6
,
⋯
X
T
=
X
⋅
(
X
2
)
⌊
T
2
⌋
T
∈
1
,
3
,
5
,
⋯
X^T=(X^2)^{\frac{T}{2}}\enspace T \in {2, 4, 6, \cdots}\\ X^T=X\cdot (X^2)^{\lfloor \frac{T}{2} \rfloor}\enspace T \in {1, 3, 5, \cdots}\\
XT=(X2)2TT∈2,4,6,⋯XT=X⋅(X2)⌊2T⌋T∈1,3,5,⋯
依次递推,我们可以把幂运算的复杂度,从
O
(
n
)
O(n)
O(n)降低到
O
(
l
o
g
2
n
)
O(log_2n)
O(log2n)。
而我们又知道矩阵乘法运算是符合结合律的,所以可以使用快速幂。
代码实现
实现2阶矩阵
这里我们简单用一维列表来表示 2 ⋅ 2 2\cdot2 2⋅2矩阵,重载加减乘运算符,并用快速幂重载幂运算运算符。
class matrix:
def __init__(self, list:list):
self.number = [0, 0, 0, 0]
self.number[0] = list[0]
self.number[1] = list[1]
self.number[2] = list[2]
self.number[3] = list[3]
def __add__(self, other):
return matrix([self.number[0] + other.number[0], self.number[1] + other.number[1], self.number[2] + other.number[2], self.number[3] + other.number[3]])
def __sub__(self, other):
return matrix([self.number[0] - other.number[0], self.number[1] - other.number[1], self.number[2] - other.number[2], self.number[3] - other.number[3]])
def __mul__(self, other):
'''
a0 a1 b0 b1
a2 a3 b2 b3
a0*b0+a1*b2 a0*b1+a1*b3
a2*b0+a3*b2 a2*b1+a3*b3
'''
list = [0, 0, 0, 0]
list[0] = self.number[0] * other.number[0] + self.number[1] * other.number[2]
list[1] = self.number[0] * other.number[1] + self.number[1] * other.number[3]
list[2] = self.number[2] * other.number[0] + self.number[3] * other.number[2]
list[3] = self.number[2] * other.number[1] + self.number[3] * other.number[3]
return matrix(list)
def __pow__(self, n):
if n == 0:
return matrix([1, 0, 0, 1])
if n == 1:
return self
if n % 2 == 0:
return (self * self) ** (n // 2)
else:
return self * (self * self) ** ((n - 1) // 2)
计算斐波那契数列
def getFib(n:int):
m1 = matrix([1, 1, 1, 0])
m1 = m1 ** (n-1)
m1 = m1 * matrix([1, 0, 1, 0])
return m1.number[0]
简单测试
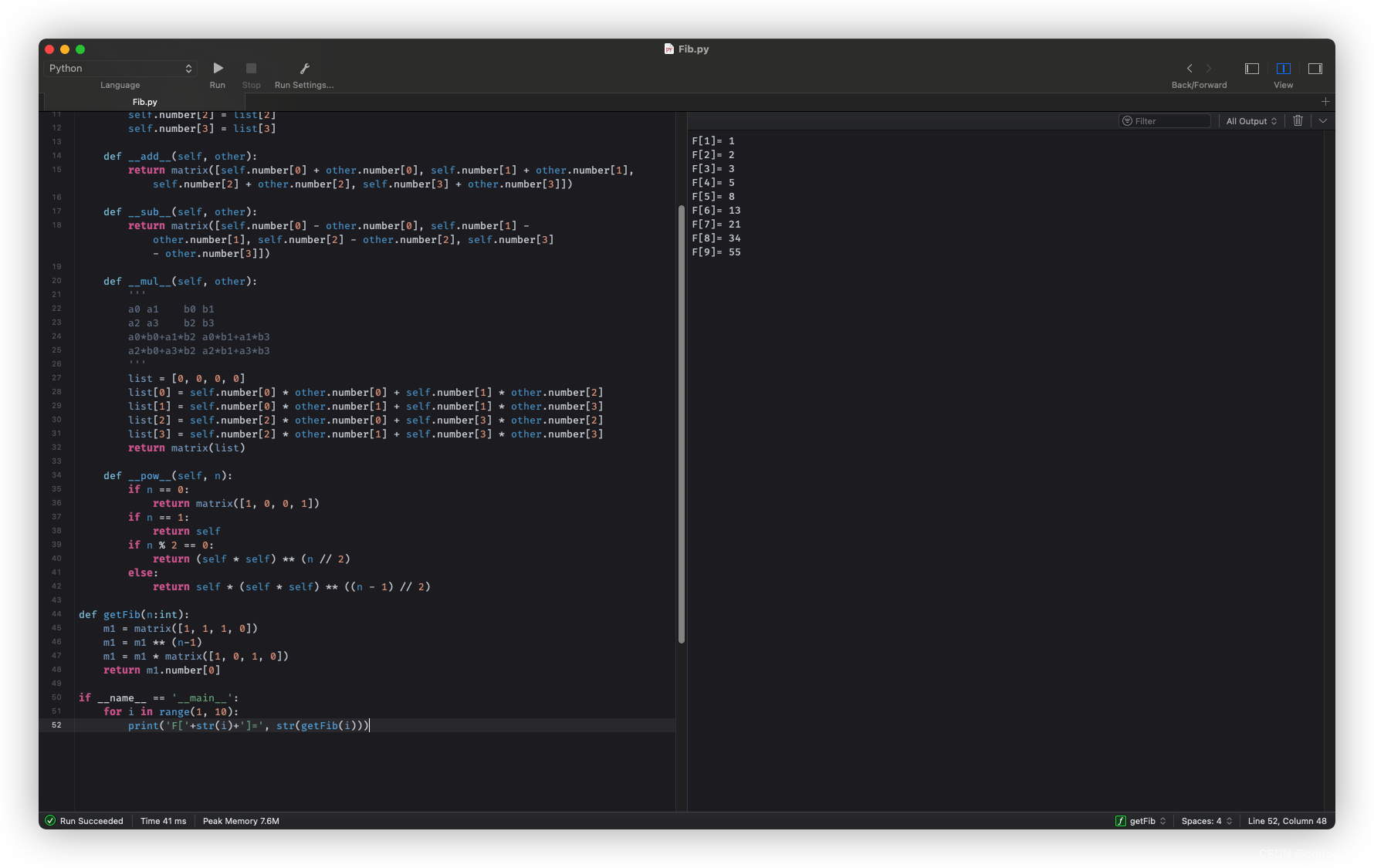
由于python中的int是不限长度的,所以可以计算比较高位,例如第10000项。
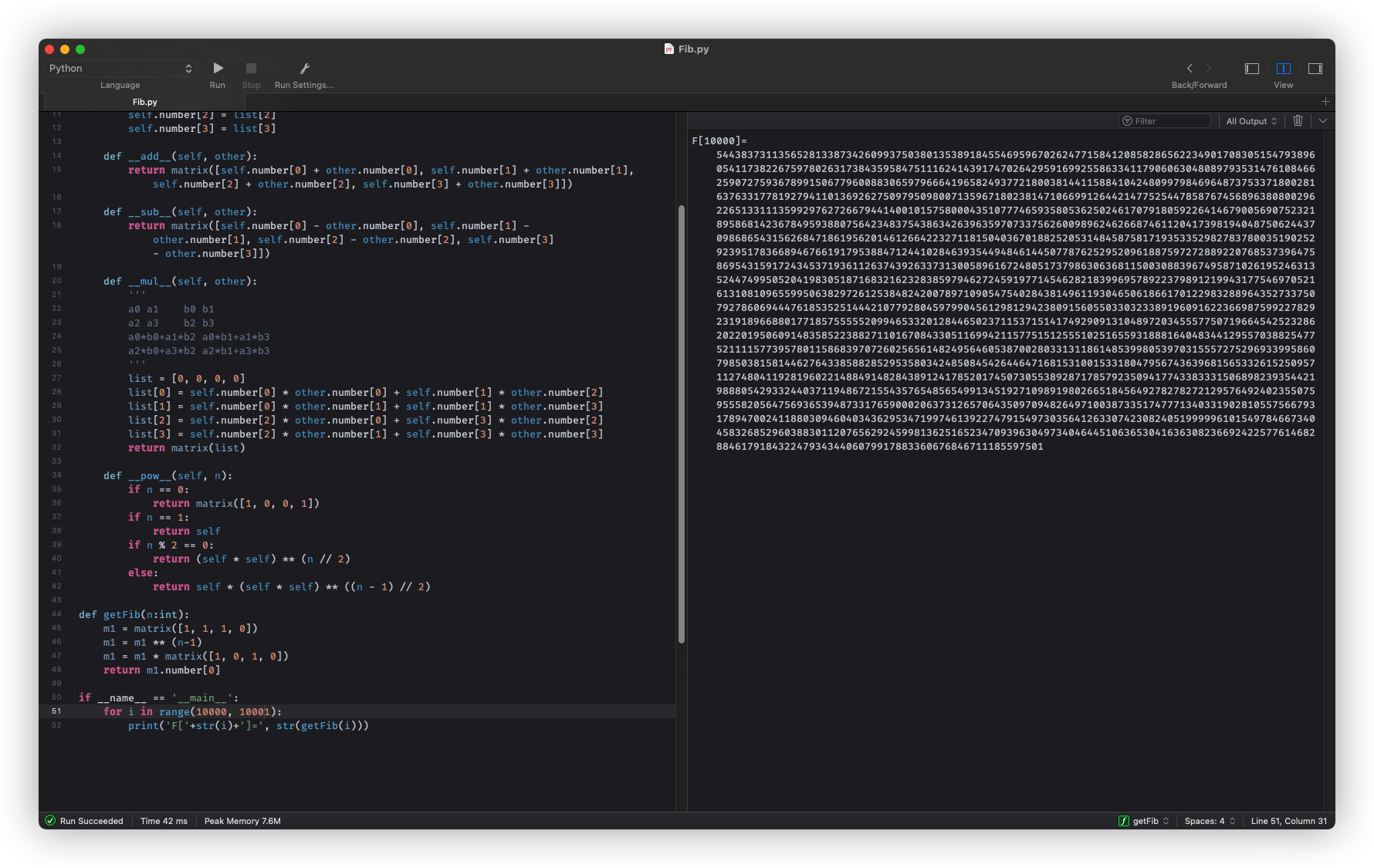
完整代码
import decimal
from decimal import Decimal
decimal.getcontext().prec = 32000
class matrix:
def __init__(self, list:list):
self.number = [0, 0, 0, 0]
self.number[0] = list[0]
self.number[1] = list[1]
self.number[2] = list[2]
self.number[3] = list[3]
def __add__(self, other):
return matrix([self.number[0] + other.number[0], self.number[1] + other.number[1], self.number[2] + other.number[2], self.number[3] + other.number[3]])
def __sub__(self, other):
return matrix([self.number[0] - other.number[0], self.number[1] - other.number[1], self.number[2] - other.number[2], self.number[3] - other.number[3]])
def __mul__(self, other):
'''
a0 a1 b0 b1
a2 a3 b2 b3
a0*b0+a1*b2 a0*b1+a1*b3
a2*b0+a3*b2 a2*b1+a3*b3
'''
list = [0, 0, 0, 0]
list[0] = self.number[0] * other.number[0] + self.number[1] * other.number[2]
list[1] = self.number[0] * other.number[1] + self.number[1] * other.number[3]
list[2] = self.number[2] * other.number[0] + self.number[3] * other.number[2]
list[3] = self.number[2] * other.number[1] + self.number[3] * other.number[3]
return matrix(list)
def __pow__(self, n):
if n == 0:
return matrix([1, 0, 0, 1])
if n == 1:
return self
if n % 2 == 0:
return (self * self) ** (n // 2)
else:
return self * (self * self) ** ((n - 1) // 2)
def getFib(n:int):
m1 = matrix([1, 1, 1, 0])
m1 = m1 ** (n-1)
m1 = m1 * matrix([1, 0, 1, 0])
return m1.number[0]
if __name__ == '__main__':
for i in range(10000, 10001):
print('F['+str(i)+']=', str(getFib(i)))