《Python数据分析基础教程：NumPy学习指南（第2版）》笔记17：第七章 专用函数3——窗函数

当前Numpy版本为：1.20

第七章 专用函数

7.23 窗函数

窗函数（window function）是信号处理领域常用的数学函数，相关应用包括谱分析和滤波器设计等。这些窗函数除在给定区间之外取值均为0。NumPy中有很多窗函数，如bartlett、blackman、hamming、 hanning和kaiser。关于hanning函数的例子可以在第4章和第3章中找到。

7.24 动手实践：绘制巴特利特窗

巴特利特窗（Bartlett window）是一种三角形平滑窗。按如下步骤绘制巴特利特窗。

• (1) 调用NumPy中的bartlett函数，以计算巴特利特窗。

  import numpy as np
  window = np.bartlett(42)
  

• (2) 使用Matplotlib绘制巴特利特窗，非常简单。

  from matplotlib.pyplot import plot, show
  plot(window)
  show()
  

绘制结果如下图所示，形状确实为三角形。

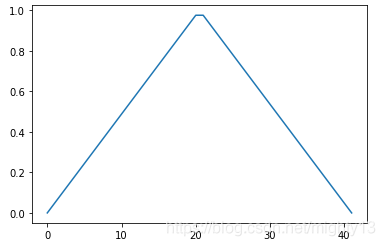
7.25 布莱克曼窗

布莱克曼窗（Blackman window）形式上为三项余弦值的加和，如下所示：

NumPy中的blackman函数返回布莱克曼窗。该函数唯一的参数为输出点的数量。如果数量为0或小于0，则返回一个空数组。

7.26 动手实践：使用布莱克曼窗平滑股价数据

我们对AAPL股价的小数据文件中的收盘价数据进行平滑处理。完成如下步骤。

• (1) 将数据载入NumPy数组。调用blackman函数生成一个平滑窗并用它来平滑股价数据。

  import numpy as np
  from matplotlib.pyplot import plot, show, legend
  from matplotlib.dates import datestr2num
  import sys
  closes=np.loadtxt('AAPL.csv', delimiter=',', usecols=(6,),
  converters={1:datestr2num}, unpack=True)
  N = 5
  window = np.blackman(N)
  smoothed = np.convolve(window/window.sum(), closes, mode='same')
  

• (2) 使用Matplotlib绘制平滑后的股价图。在这个例子中，我们将省略最前面5个和最后面5个数据点。这是由于存在很强的边界效应。

  plot(smoothed[N:-N], lw=2, label="smoothed")
  plot(closes[N:-N], label="closes")
  legend(loc='best')
  show()
  

经过布莱克曼窗平滑后的AAPL收盘价数据如下所示。

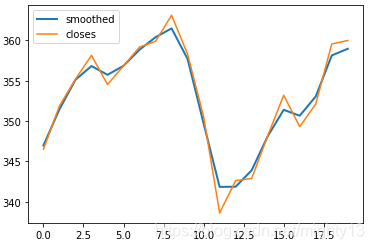
7.27 汉明窗

汉明窗（Hamming window）形式上是一个加权的余弦函数。公式如下所示。

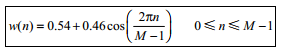
NumPy中的hamming函数返回汉明窗。该函数唯一的参数为输出点的数量。如果数量为0或小于0，则返回一个空数组。

7.28 动手实践：绘制汉明窗

我们来绘制汉明窗。完成如下步骤。

• (1) 调用hamming函数，以计算汉明窗：

  import numpy as np
  from matplotlib.pyplot import plot, show
  
  window = np.hamming(42)
  

• (2) 使用Matplotlib绘制汉明窗：

  plot(window)
  show()
  

  绘制结果如下图所示。

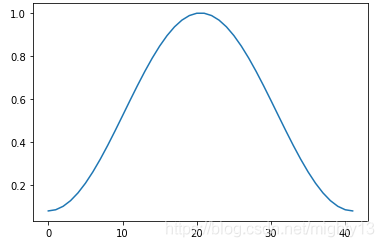
7.29 凯泽窗

凯泽窗（Kaiser window）是以贝塞尔函数（Bessel function）定义的，公式如下所示。

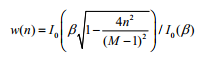
这里的I₀即为零阶的贝塞尔函数。 NumPy中的kaiser函数返回凯泽窗。该函数的第一个参数为输出点的数量。如果数量为0或小于0，则返回一个空数组。第二个参数为β值。

7.30 动手实践：绘制凯泽窗

我们来绘制凯泽窗。完成如下步骤。

• (1) 调用kaiser函数，以计算凯泽窗：

  import numpy as np
  from matplotlib.pyplot import plot, show
  
  window = np.kaiser(42, 14)
  

• (2) 使用Matplotlib绘制凯泽窗：

  plot(window)
  show()
  

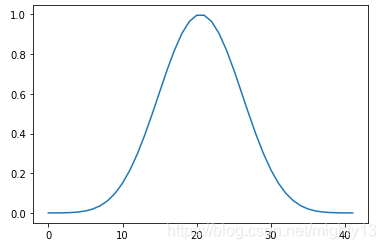
绘制结果如下图所示。

7.31 专用数学函数

贝塞尔函数（Bessel function）是贝塞尔微分方程的标准解函数（详见https://baike.baidu.com/item/贝塞尔函数）。在NumPy中，以i0表示第一类修正的零阶贝塞尔函数。

7.32 动手实践：绘制修正的贝塞尔函数

我们来看看第一类修正的零阶贝塞尔函数绘制出来是什么形状。

• (1) 使用NumPy的linspace函数生成一组均匀分布的数值。

  import numpy as np
  from matplotlib.pyplot import plot, show
  x = np.linspace(0, 4, 100)
  

• (2) 调用i0函数进行计算：

  vals = np.i0(x)
  

• (3) 使用Matplotlib绘制修正的贝塞尔函数：

  plot(x, vals)
  show()
  

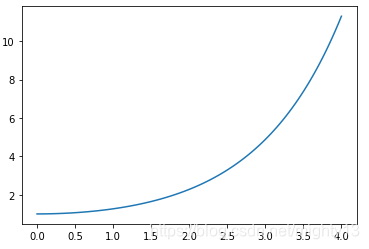
绘制结果如下图所示。

7.33 sinc 函数

sinc函数在数学和信号处理领域被广泛应用。 NumPy中有同名函数sinc，并且也存在一个二维版本sinc2d。 sinc是一个三角函数，更多详细内容请访问https://baike.baidu.com/item/sinc函数。

7.34 动手实践：绘制 sinc 函数

我们将绘制sinc函数。完成如下步骤。

• (1) 使用NumPy的linspace函数生成一组均匀分布的数值。

  import numpy as np
  from matplotlib.pyplot import plot, show
  x = np.linspace(0, 4, 100)
  

• (2) 调用sinc函数进行计算：

  vals = np.sinc(x)
  

• (3) 使用Matplotlib绘制sinc函数：

  plot(x, vals)
  show()
  

绘制结果如下图所示。

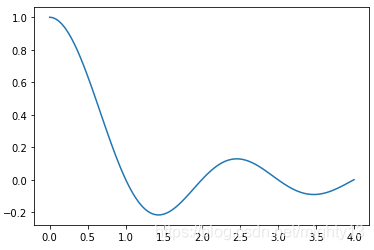
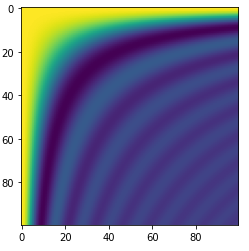
sinc2d函数需要输入一个二维数组。我们可以用outer函数生成二维数组，便得到下图。

import numpy as np
from matplotlib.pyplot import imshow, show

x = np.linspace(0, 4, 100)
xx = np.outer(x, x)
vals = np.sinc(xx)

imshow(vals)
show()