D. Count the Arrays----------------------------(思维)组合数学

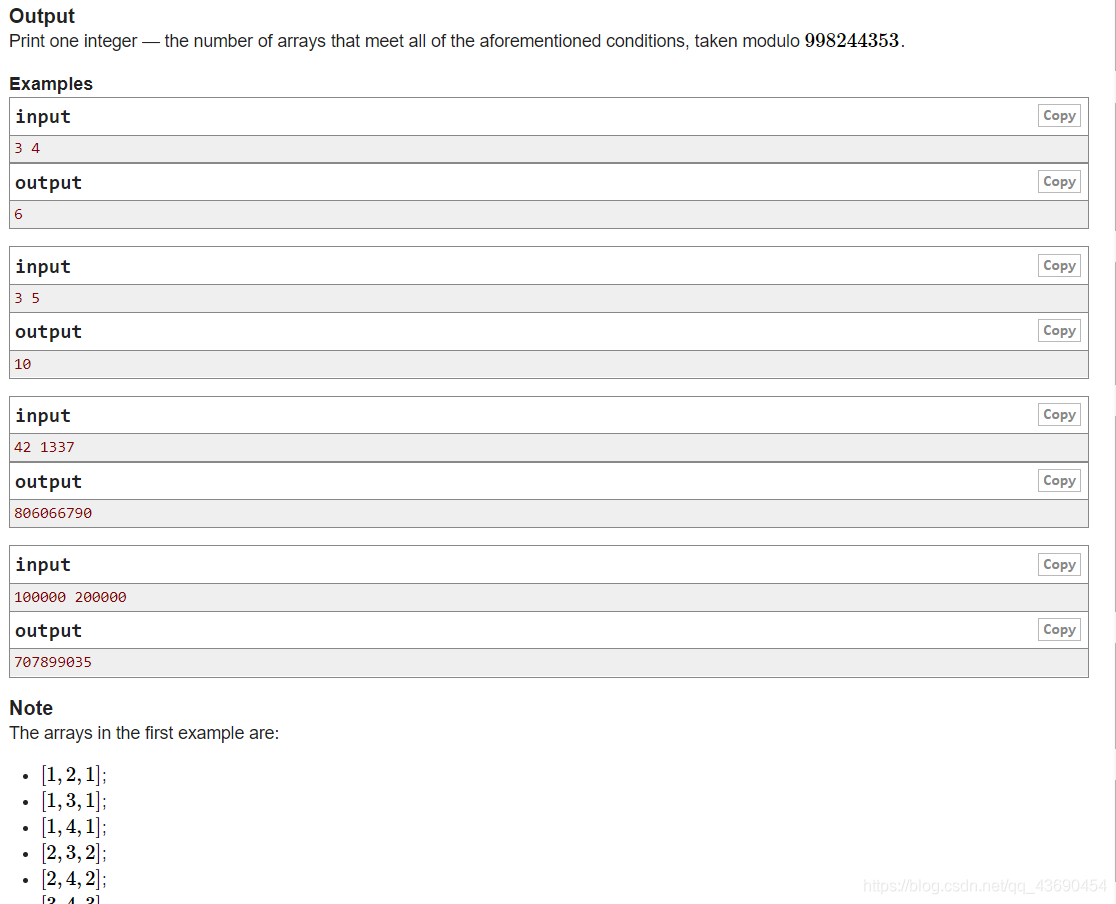
题意:
从1-m种选n个数出来，组成一个数组要满足一下三个条件
1.1<=ai<=m
2.恰好有一对元素相等
3.aj<aj+1 if j<i 且 aj>aj+1 if j>=i

问存在多少种这种组合

解析:
第一步: 我们要从m个数种选出n-1个(因为存在一对元素相同)C(m,n-1)
第二步: 假设最大值在i这个位置上，我们要把那一对相同的元素放到最大值两边取。那么i的左边要从n-2 (除去最大值) 个数中取i-2个(因为存在一对相同的在i的右边出现过，左边自然出现)所以只要取i-2个数，也就是C(n-2,i-2),那么右边自然有(n-i)个数。

组合公式就是:C(m,n-1)*C(n-2,i-2) * (n-i)

第三步: 枚举最大值的位置 2~n-1

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+1000;
const int MOD=998244353;
ll fact[N];
int n,m;
void init()
{
	fact[0]=1;
	for(int i=1;i<=N;i++) fact[i]=(fact[i-1]*i)%MOD;
}
ll quick(ll a,ll b)
{
	ll res=1;
	while(b)
	{
		
		if(b&1) res=res*a%MOD;
		a=a*a%MOD;
		b>>=1;
	}
	return res;
}
ll C(int a,int b)
{
 
	return fact[a]*quick(fact[b]*fact[a-b]%MOD,MOD-2)%MOD;
}
int main()
{
	init();
	scanf("%d %d",&n,&m);
	
	ll ans=0;
	for(int i=2;i<=n-1;i++)
	{
		ans=(ans+C(m,n-1)%MOD*C(n-2,i-2)%MOD*(n-i)%MOD)%MOD;
	}
	cout<<ans<<endl;
 }