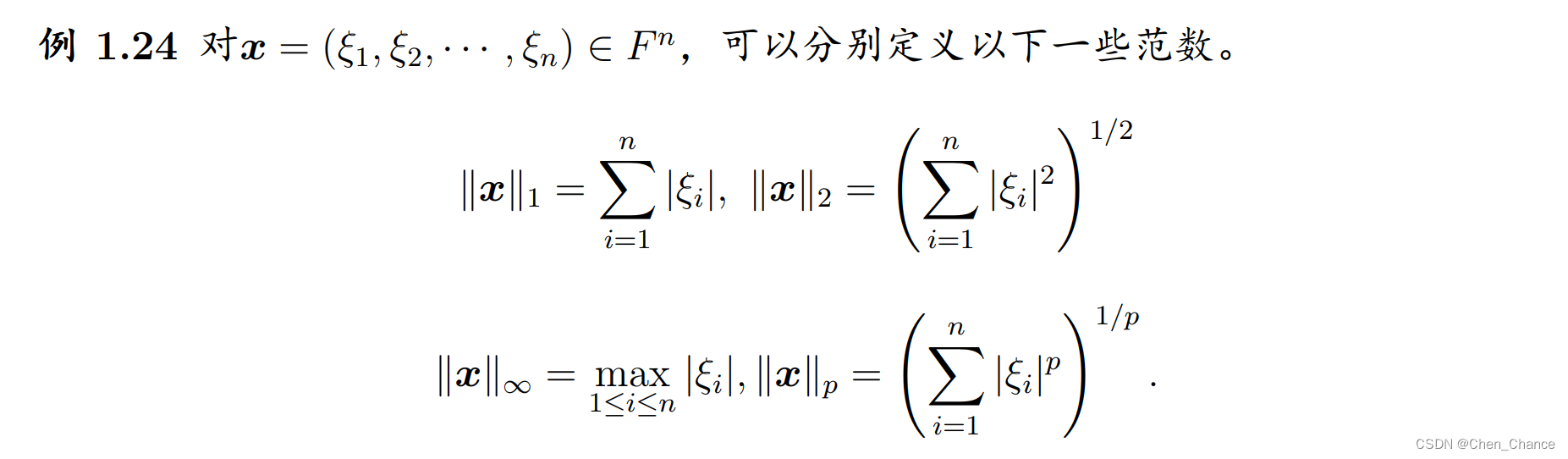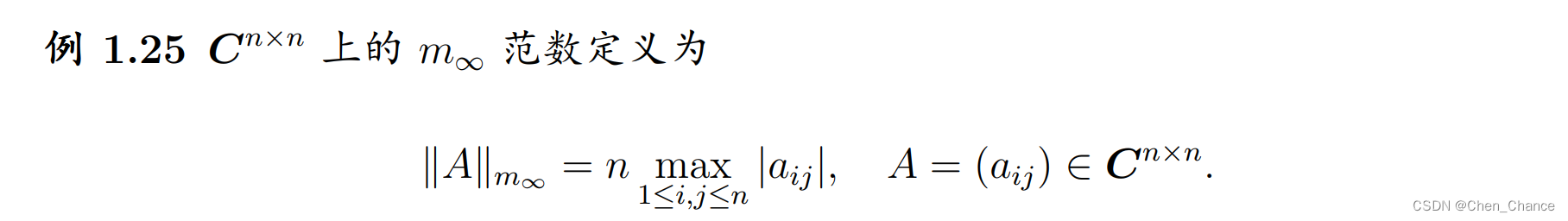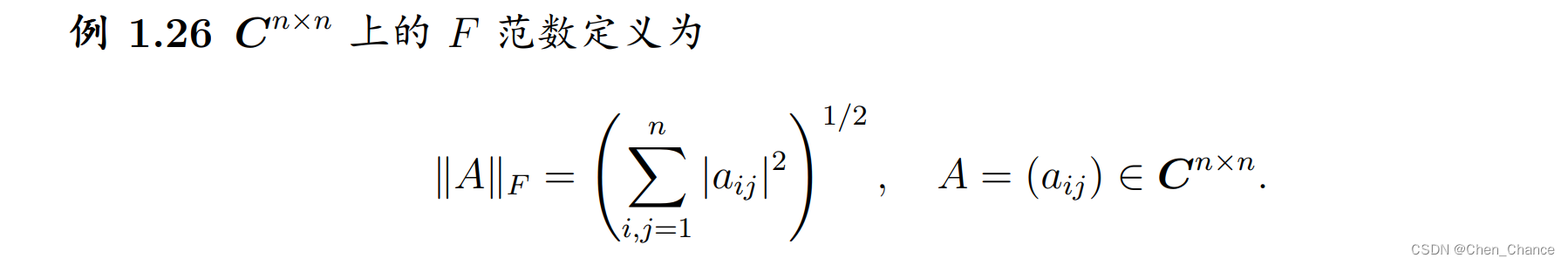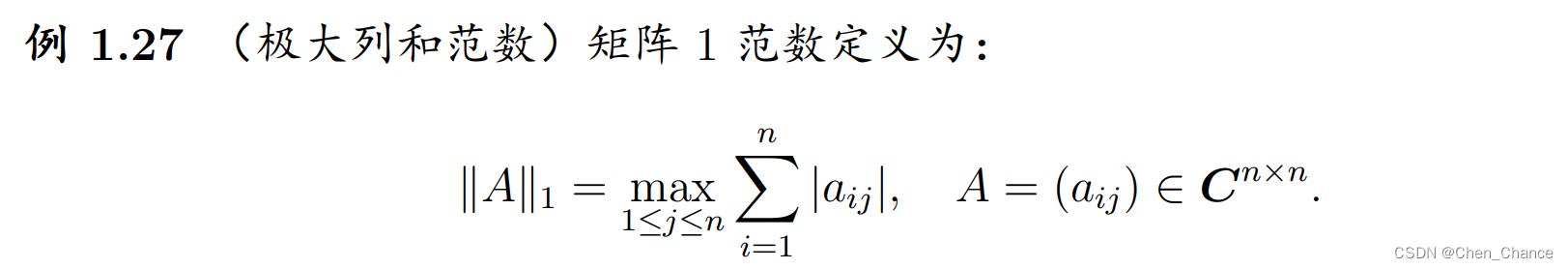向量范数和矩阵范数(L1范数和L2范数)

向量范数

L1范数

权重向量 $w$ 的 L1 范数，也称为曼哈顿范数或 1-范数，是一个向量的长度或模的度量。它的定义如下：

对于一个 n 维的实数向量 $w=[w_1,w_2,...,w_n]$，其 L1 范数（Manhattan 范数）表示为：

$$\Vert w{\Vert }_1=|w_1|+|w_2|+...+|w_n|$$

其中 $\Vert w{\Vert }_1$ 表示 $w$ 的 L1 范数，$w_i$ 表示向量 $w$ 的第 i 个分量。

L1 范数实际上是向量 $w$ 的各个分量的绝对值之和。与 L2 范数不同，L1 范数更加注重向量中每个分量的绝对大小，而不是它们的平方。

在机器学习中，L1 范数也常常用作正则化项的一部分，以限制模型参数的大小，防止过拟合。当我们希望模型的参数不仅小，而且尽可能稀疏时，可以在损失函数中添加 $\Vert w{\Vert }_1$ 作为正则化项。L1 正则化有助于将某些模型参数推向零，从而实现特征选择（feature selection），即选择对任务最重要的特征。这对于高维数据的处理和模型解释非常有用。

L2范数

权重向量 $w$ 的 L2 范数，也称为 Euclidean 范数或 2-范数，是一个向量的长度或模的度量。它的定义如下：

对于一个 n 维的实数向量 $w=[w_1,w_2,...,w_n]$，其 L2 范数（Euclidean 范数）表示为：

$$\Vert w{\Vert }_2=\sqrt{w_1^2+w_2^2+...+w_n^2}$$

其中 $\Vert w{\Vert }_2$ 表示 $w$ 的 L2 范数，$w_i$ 表示向量 $w$ 的第 $i$ 个分量。

L2 范数实际上是向量 $w$ 到原点的欧几里德距离，它是向量 $w$ 的各个分量的平方和的平方根。L2 范数通常用于表示向量的长度或模，它的值永远是非负的。

在机器学习中，L2 范数常常用来作为正则化项的一部分，以限制模型参数的大小，防止过拟合。当我们希望模型的参数不要过大时，可以在损失函数中添加 $\Vert w{\Vert }_2$ 作为正则化项，从而鼓励模型选择较小的参数值。这有助于提高模型的泛化性能。

矩阵范数

在数学中，$||A||$ 通常表示矩阵$A$ 的范数（Norm）。矩阵的范数描述了矩阵的某种度量，可以理解为衡量矩阵大小或长度的一种方式。不同的范数有不同的定义，常见的包括 Frobenius 范数、1-范数、2-范数等。

• Frobenius 范数（Frobenius Norm）：
  对于一个矩阵 $A$，其 Frobenius 范数定义如下：

$$||A|{|}_F=\sqrt{\sum _{i=1}^N\sum _{j=1}^N|a_{ij}{|}^2}$$

其中$a_{ij}$是矩阵$A$中的元素。

• 1-范数（1-Norm）：
  矩阵$A$的 1-范数是矩阵列绝对值元素之和的最大值。

• 2-范数（2-Norm）：
  矩阵$A$的 2-范数是矩阵的最大奇异值（即矩阵的特征值的平方根）。

这些范数可以用来衡量矩阵在不同情况下的大小、稳定性和其他性质。具体使用哪种范数取决于应用场景和需要分析的特定方面。

总结