因果学习的三个层次

来源:混沌巡洋舰
昨天龚鹤扬博士在集智的讲座因果学习综述,我借此机会结合我的理解给大家总结客串下这个讲座,和因果学习的核心内容,及巡洋舰一段时间关于因果的文章汇总。
这个讲座分为三部分,第一是什么因果及其哲学基础,第二是统计学中的因果, 第三是机器学习中的因果。
一, 哲学中的因果以及因果科学的定义
因果已经成为我们最重要的认知工具, 而且被认为是下一代AI革命的重要引擎之一。那么究竟什么是因果?用一句话说:因果是当某个变量T改变的时候,在保持其它变量不变的时候, 它是如何导致另一个变量Y改变的(由此我们看出因果的有向性,因果可以独立作用)。
即使是从这个定义里我们也可以立刻看到,如果和相关性进行比较, 我们看到这里的区别一在于改变, 二在于其它变量不变, 这就是说英国是A到B产生的效应,而非仅仅是A
和B的关联, 它具有明确的方向性和干预属性。这种定义的方法包含了干预主义的核心思想,因此也称为interventionist

而古往今来的哲学讨论里,另一个核心观点在于反事实的因果观念, 这个观念说的是当假设过去的其它事情不发生,是否有一个因子导致了最终的结果不会发生。这里我立刻想到类似于法律案件判断的一种基本思维,那就是指定某个人有罪与否的通常思维是假定他没有做出某个行为最后罪行的结果还是否会出现。
然而这种因果思维通常存在严重的漏洞,比如下面的例子:

A和B一起用石头扔瓶子,A的石头恰好击中了瓶子碎了。那么如果A不去用石头打瓶子似乎它也会碎, 你可以因此去说A的石头不是瓶子碎的原因吗?如果我们深思,类似的悖论还很多, 比如你和你女友n次吵架最后分手了, 那么如果没有第n次吵架你们也许不会分手, 你可以说第n次吵架就是分手的原因吗?
因此对于因果问题的定义是一个细思恐极的事情,我们看似懂了实际不懂。然而只要它是一种方便的思维工具, 我们还会每天不假思索的用下去而且不着急。事实上唯一严格定义清晰的因果是在物理学, 物理学的因果的基础是相互作用, 而相互作用的结果只有最终在时间维度上体现, 这和我们日常方便性的因果有着本质的区别。
一个有趣的总结是我们可以把因果分成两类,一个是type causality,一个是actual causality。第一类比较类似自然科学的因果,或者某种事物作用和变化的机制, 比如滥发钞票导致通货膨胀。而另一个则和我说的现实生活中的那些鸡毛蒜皮小事的直接原因,比如刚刚举的吵架导致分手。

最终我对这里的总结是, 因果是一种工具,追求严格定义没有意义,而是取决于使用的语境。
想要初步了解因果的定义,哲学含义,我们为什么需要因果, 巡洋舰积累了不少素材,尤其是围绕Pearl的 重磅级著作 《为什么》
二, 统计学上的的因果推断
假定你手里有若干变量的一堆数据,你希望从这些变量里提取出一组因果关系。这你就要做的事情是因果推断。贯穿所有因果问题共通的地方是Judea Pearl的三层框架 ,我们要在我们手里的观察数据里求解出下面三个层次。
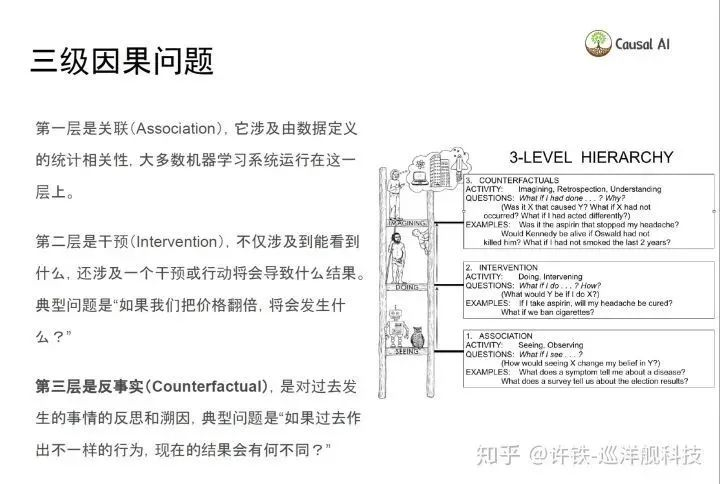
事实上为了做到这件事我们可以采用一个非常统一一致的流程,讲这个问题过于枯燥, 这里新冠病毒死亡率是一个极好的例子, 我们知道意大利的新冠病毒死亡率高于中国, 而这是否说明意大利的医疗治愈情况弱于中国呢?好了我们用统计的方法来回答下这个问题:
1, 定义问题,把问题和已知信息转化为因果图,这个图一般是coase-grain的世界模型, 把统计上复杂的分布化作一个节点。其实这一步是非常难的,难就在确定问题相关的因子有哪些,表面上这里只有国家和死亡率两个节点,但是事实上潜在的影响因素有很多,比如年龄,性别,教育程度, 如果你仔细去研究这个问题可能要包含了社会的所有方面。所以这里抬出了统计物理的一个基本思想coase-grain,我们把问题粗粒化最后留下最重要的。最终这里选择了国家,年龄结构和死亡率这三个因素,因为年龄对死亡的影响其实比较显著。比如看下图
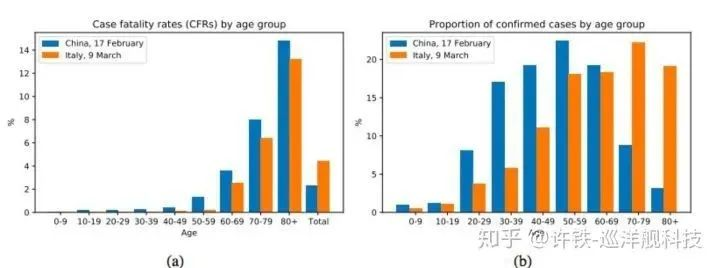
2, 形成因果图, 这个因果图一般包含treatment和output, 以及其它的confounder
我们把年龄,国家和死亡率三个要素画出下图的三角C代表国家,A代表年龄,M代表死亡率 然后分析这个图里的因果关系,我们看到国家通过年龄结构影响死亡率,起到了中介变量的作用,因为年纪越大的人死亡率越高。而如果需要分析单纯国家对死亡率的影响(这里包含很多因素,比如国家的医疗条件,空气污染程度),则需要阻断A来分析C到M的影响。

3, 这里就要给出和因果分析和力学里的牛顿第二定律般的do calculus。这里的思维本质就是干预,既然年龄是一个重要的中介因子, 而两个国家的年龄又是不同的。我们如果要求得单纯国家这个因素对死亡率的影响,就要把年龄这个因素控制成一样,来求解国家不同对死亡率的影响。具体的做法是把年龄分布(年龄相对国家的条件概率)假定成相同,求两个不同国家的死亡率在这个相同分布下的期望, 并取其差值。这个控制也可以看作是阻断,它阻断了国家对年龄变量的影响。最终得到了结果的确是意大利的死亡率更低!

4, 另一方面,我们可以计算由中介因子带来的间接因果效应(年龄的影响)
这一次我们要的控制的是国家这个变量, 也就是假定不同年龄段的死亡率在两个国家是相同的(以中国为标准), 看不同年龄分布对死亡概率的影响。

这里我们还观测到的有趣现象是直接因果效应和间接因果效应的和不等于死亡率, 这也暗示了这两个因子存在某种相互作用效应。
事实上统计里的因果推断的关键是消除各种偏差,这些偏差往往是因为已知或未知的中间因子的存在导致x到y的因果效应难以衡量, 比较有名的有confounder bias , selection bias, 而识别这些偏差关键是寻找不同因子背后的因果图连接(如下),阻断那些非直接的联系。

龚老师还推荐了几个非常优秀的文献:
1, Causal inference, Hernán M. A., Robins J. M. 一个非常易懂的入门手册
2, The handbook of graphical models(2018) 围绕统计因果学习的工具核心-图模型
3, Causal Inference for Statistics, Social, and Biomedical Science
介绍几种常见的因果悖论
相关性和因果性的比较
用因果的视角看三门问题, 并用此分析华为应对美国制裁的策略
介绍几种常见的统计因果分析方法
非常实用的因果推理入门手册含代码
三,基于因果的人工智能, Causal AI
这一定是如今大部分人都关注的问题, 当下的机器学习缺少因果思维, 刚刚的因果统计能否在这里助力?首先当下的AI缺少因果这一层次,即使是GPT-3这样复杂的模型, 事实上也仅仅是相关性的体现。
基于因果的人工智能一个重要体现是小图灵测试 - 也就是如何让机器来表征因果知识, 然后回答问题 。如果机器能够做到这一点,无疑是和人的接近程度大大接近。

如何让机器具备因果思维, 事实上依然是围绕如何让机器学习刚刚讲的三级因果关系, 关联, 干预 和 反事实。大家注意反事实问题在以统计为基础的机器学习里是很困难的。
这时候我们来套用机器学习的典型思维,输入一大堆数据,算法就可以推断某件事的前因后果,进行反事实推理。
这台机器就叫做因果推理引擎, 它是一个包含问题,到模型(图模型)到求解答案全过程的机器。这台机器的输入是问题,数据和假设(对核心变量因果关系的先验),把它们转化为包含因子和边的图模型(因果问题的语言), 最终通过结构方程得到需要求解问题的干预概率(do - calculus),或反事实问题(counter-factual)。
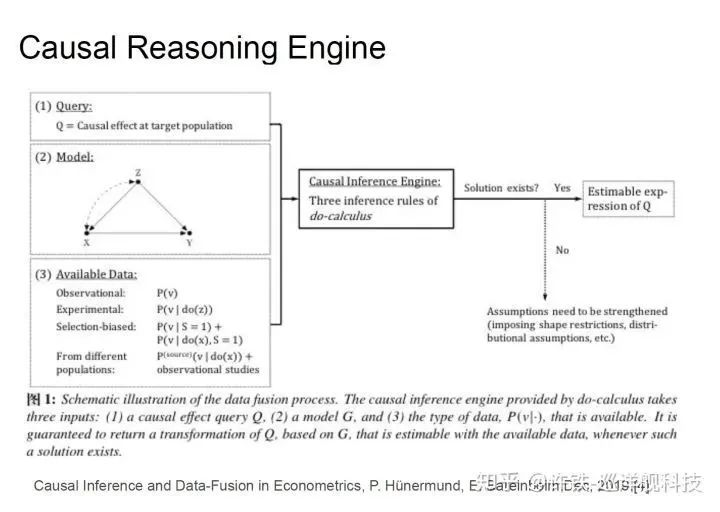


因果推理引擎可以被归纳在结构因果模型里, 这个模型就是包含节点和边的图模型,但是与之不同的是 , 结构模型用结构方程而不是条件概率描述节点和节点的关系,而是用函数形式,X = f(PA,U) PA是一组决定结果的因子, U代表未知的外界随机变量,这个定义使得因果关系的定义更加灵活,也更符号机器学习语言,同时包含条件概率对不确定性的表达能力。
以下是结构因果模型的一个基本形式,我们非常容易看到它的构建是首先需要把所研究问题的核心变量表达成一个图结构,这里研究的是当你发现草坪湿润了,你要找到这个现象背后的原因。比如气候, 洒水机工作,或者下雨。这个问题的难点在于因果关系盘根错节, 比如下雨,洒水和草坪湿润之间存在已知的因果关系(先验), 而气候又影响这两者。熟悉贝叶斯概率图模型的同学一定会熟悉这个图。这里唯一的区别是贝叶斯的条件概率被替换成为结构方程。
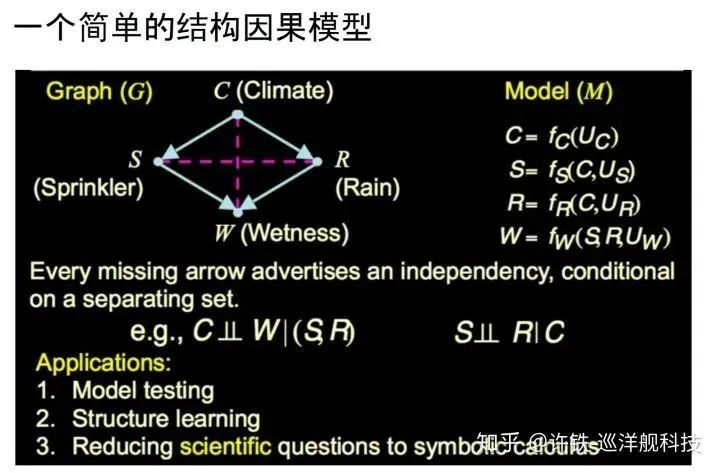
事实上结构方程肯定不是唯一的因果关系的表达形式, 比如动力学方程组组也可以刻画系统内的因果关系。相比动力学方程组结构因果模型的最大缺点是基于有向无环图DAG , 而对带有循环的图缺少表示能力, 动力学方程则可以。然而结构方程的形式却更加容易直接做成do calculus,同时结构因果模型也包含了某种世界运行的机理和数据生成的机制,虽然不似微分方程精确。
关于结构方程的好处最好的解释在CAUSALITY FOR MACHINE LEARNING 这篇文章里。作者写到了它和do calculus的内在联系, 以及它如何导致一个因子化的概率表示。

具体有了结构方程后,我们需要的依然是用因果分析的牛顿第二定律- do calculus来求解我们需要的干预条件概率。当然在一个复杂的因果图里节点的数量非常多, 为了分析问题的方便, 我们需要动用d-separation条件独立性, 也就是当阻断了X和Y间的中间路径(d-separate)使得X,Y变为条件独立。具体阻断的方法是阻断某个发射节点(影响x和y的共因)而同时不可以阻断接收节点(否则引入一个额外的相关性)就是下面的1条和2条。

得到d-separation之后, 我们就得到一组条件独立性,帮我们来去掉do calculus一些不必要的中间变量, 从而更好的计算干预性问题。

再看反事实推理, 有了结构因果方程,我们就可以得到如下的反事实推理步骤, 1, 溯因:
通过已知的当下结果(x,y)更新结构方程 2, 更换:把之前结构方程的事实X更换为x 3
预测:使用更新后的结构方程得到如果过去的事实按照x发生,则最终的结局 y。
大家注意反事实推理的巨大意义,它事实上是用数据反推一个世界模型,包含那些agent从未经历的状态, 从而可以在这个模型里想象无穷多的平行世界。

把因果引入机器学习将可以解决机器学习里一些最重要的困境, 比如缺少鲁棒性,无法进行外推式的泛化(就是求解数据集分布外的情况), 缺少可解释性等。而基于因果的AI某种程度都是对这些问题的对症下药, 首先,基于因果的AI掌握了一个结构方程模型,可以进行反事实推理,这本质是在解决外推问题, 掌握了因果的模型将更难被噪声干扰因为它某种程度掌握数据生成的规律, 同时有因果的模型更加符号人类认知因而更具有可解释性。

在有关因果的人工智能方面, 巡洋舰也积累了很多素材:
为了研究因果关系,原来科学家在这么多方向上都有尝试
维融入机器学习,实现信息处理的自动化
强人工智能之路中的必选项“因果”-《为什么》第十章书摘 Part1
让神经网络变得透明-因果推理对机器学习的八项助力
未来智能实验室的主要工作包括:建立AI智能系统智商评测体系,开展世界人工智能智商评测;开展互联网(城市)云脑研究计划,构建互联网(城市)云脑技术和企业图谱,为提升企业,行业与城市的智能水平服务。
如果您对实验室的研究感兴趣,欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”

