一阶动量和二阶动量及Adam等优化算法笔记
就按照
从动量和矩的角度探讨优化理论的内涵(以动量法、AdaGrad和Adam举例) - 知乎
的讲解学习,讲的挺细的。这里补充一些笔记方便以后自己复习用。
1.AdaGrad算法
其中说到了“如果目标函数有关自变量中某个元素的偏导数一直都较大,那么该元素的学习率讲下降较快;反之,如果目标函数有关自变量中某个元素的偏导数一直都较少,那么该元素的学习率将下降较慢”。我认为这是站在SGD的角度来看的。
SGD的梯度更新如下
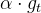
对于SGD来说,其学习率一直是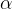 ,然后相较之下AdaGrad算法的学习率:
,然后相较之下AdaGrad算法的学习率:
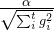
这样看AdaGrad算法的学习率确实非递增。而且,偏导越大学习率下降就越快,偏导越小学习率下降就越慢。
2.Adam算法
对于文中说的一阶动量和二阶动量,我算了一下,没对上,可能是作者笔误或我疏忽了。
根据文中说的:
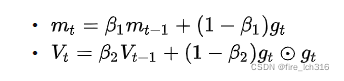
我这边按照上面两个公式算的是:
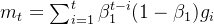
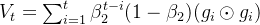
这样的话,系数求和就是等比数列求和:
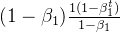
这样除以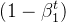 就变成1了。
就变成1了。
其次就有期望:
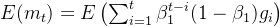
然后这里把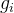 看成独立同分布,就有:
看成独立同分布,就有:

然后所有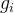 的期望就都一样了,带入求和,用等比数列求和得:
的期望就都一样了,带入求和,用等比数列求和得:
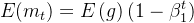
这样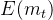 除以
除以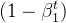 就等于
就等于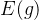 了。
了。
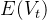 同理。
同理。