常用排序算法
一、冒泡排序(稳定)
原理:通过重复的遍历未排序的数组,一次比较两个元素,如果它们顺序错误就交换,直到遍历数组没发现要交换的元素,排序就完成了。
void Swap(int& num1, int& num2) {
int temp = num1;
num1 = num2;
num2 = temp;
}
void BubbleSort(int* arr, int len) {
if (!arr) return;
for (int i = 0; i < len - 1; i++) {
bool tag = true;
for (int j = 0; j < len - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
Swap(arr[j], arr[j + 1]);
tag = false;
}
}
if (tag)break;
}
}
二、选择排序(不稳定)
原理:遍历数组,找出最小(大)值,放在数组首(尾),然后遍历剩下的无序的数组,重复这一步骤。
void Swap(int& num1, int& num2) {
int temp = num1;
num1 = num2;
num2 = temp;
}
//降序
void SelectSort1(int arr[], int len) {
if (!arr)return;
for (int i = 0; i < len - 1; i++) {
int max = 0;
for (int j = 0; j < len - i; j++) {
if (arr[j] > arr[max]) {
max = j;
}
}
if (max != len - i - 1) {
Swap(arr[max], arr[len - i - 1]);
}
}
}
//升序
void SelectSort2(int arr[], int len) {
if (!arr)return;
for (int i = 0; i < len - 1; i++) {
int min = i;
for (int j = i; j < len; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
if (min != i) {
Swap(arr[min], arr[i]);
}
}
}
三、插入排序(稳定)
原理:先认为数组第一个元素是有序的,然后将后面的一个元素与前面有序的元素从后往前依次比较(比较过程与冒泡排序类似)。重复以上步骤,直到数组有序。
void Swap(int& num1, int& num2) {
int temp = num1;
num1 = num2;
num2 = temp;
}
void InsertSort(int arr[], int len) {
if (!arr) return;
for (int i = 1; i < len; i++) {
int index = i;
for (int j = i-1; j >= 0; j--) {
if (arr[j] > arr[index]) {
Swap(arr[j], arr[index]);
index = j;
}
}
}
}
四、希尔排序(不稳定)
原理:它是优化后的插入排序,在某些极端情况下,比插入排序更快。与插入排序不同是是它有一个增量。
1、选择增量,一般选择gap=len/2
2、按增量将数组分成若干个子数组
3、对每一个子数组进行插入排序
4、缩小增量gap=gap/2
5、重复2、3、4,当增量为0时,排序完成
void Swap(int& num1, int& num2) {
int temp = num1;
num1 = num2;
num2 = temp;
}
void ShellSort(int arr[], int len) {
if (!arr) return;
for (int gap = len / 2; gap > 0; gap = gap / 2) {//当增量为1的时候,就是普通的插入排序。然后增量变为0,排序结束
for (int i = gap; i<len; i++) {//依次对每一组数据进行插入排序
int index = i;
for (int j = i - gap; j >= 0 && arr[j] > arr[index]; j = j - gap) {
Swap(arr[j], arr[index]);
index = j;
}
}
}
}
五、堆排序(不稳定)
原理:
1、先构建一个最大堆
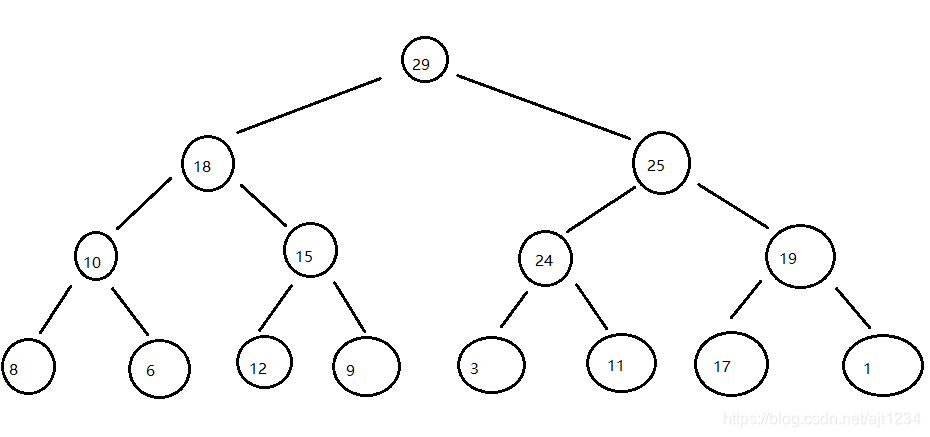
2、将堆顶元素出堆与最后一个元素交换,然后数组长度减1(一个元素已经有序了)
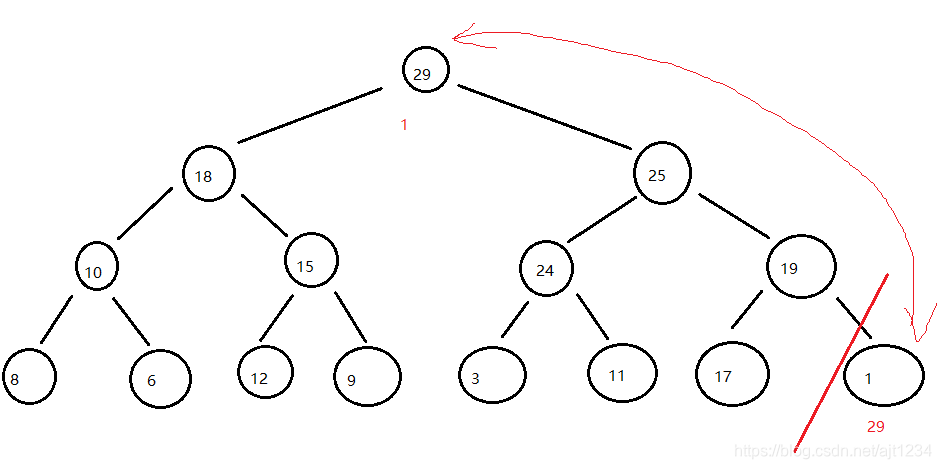
3、自上往下调整,又产生了一个新的最大堆(这里涉及到的元素交换非常少)
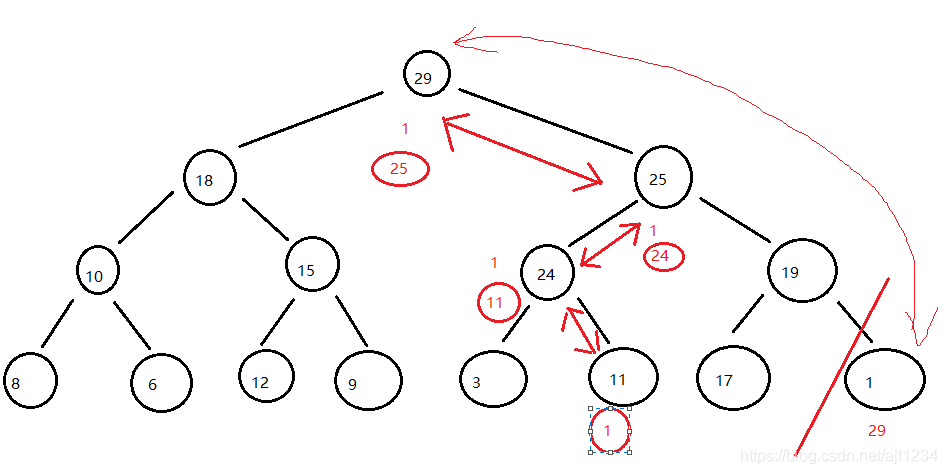
4、重复2、3,直到所有元素出堆,排序完成
void Swap(int& num1, int& num2) {
int temp = num1;
num1 = num2;
num2 = temp;
}
void BuildHeap(int arr[], int& len) {
for (int i = (len - 1) / 2; i >= 0; i--) {
JustDown(arr, len, i);
}
}
void JustDown(int arr[], int& len, int index) {
int child = 0;
for (; index * 2 + 1 < len; index = child) {
child = index * 2 + 1;
if (child + 1 < len && (arr[child] < arr[child + 1])) {
child++;
}
if (arr[index] < arr[child]) {
Swap(arr[index], arr[child]);
}
}
}
bool PopHeap(int arr[], int& len) {
if (len <= 0)return false;
Swap(arr[0], arr[--len]);
JustDown(arr, len, 0);
return true;
}
void HeapSort(int arr[], int len) {
BuildHeap(arr, len);
int size = len;
for (int i = 0; i < size; i++) {
if (!PopHeap(arr, len))return;
}
}
六、归并排序(稳定)
原理:利用分治法的思想,将一个数组分成两组,每一组再分两组…,直到每组只有一个元素,这时每一组都可以认为是有序的。然后将两组数组中的元素,按顺序依次出列,合并成一组有序的数组。最终所有数组都这样合并成一组有序的数组。
void Merge(int arr[], int L, int M, int R, int temp[]) {
if (!temp)return;
int Lmin = L; //左边最小元素的位置
int Rmin = M; //右边最小元素的位置
int k = L;
//将两个有序数组中较小的元素依次放入临时数组
while (Lmin < M && Rmin <= R) {
if (arr[Lmin] < arr[Rmin]) {
temp[k++] = arr[Lmin++];
}
else {
temp[k++] = arr[Rmin++];
}
}
//处理剩下的元素
while (Lmin < M) {
temp[k++] = arr[Lmin++];
}
while (Rmin <= R) {
temp[k++] = arr[Rmin++];
}
memcpy(arr + L, temp + L, sizeof(int) * (R - L + 1));
}
void MergeSort(int arr[], int L, int R, int temp[]) {
if (!temp)return;
if (L < R) {
int mid = L + (R - L) / 2;
MergeSort(arr, L, mid, temp);
MergeSort(arr, mid+1, R, temp);
Merge(arr, L, mid+1, R, temp);
}
}