torch.Tensor的几种乘法介绍

点乘

a与b做*乘法，原则是如果a与b的size不同，则以某种方式将a或b进行复制，使得复制后的a和b的size相同，然后再将a和b做element-wise的乘法。

* 标量

Tensor与标量k做*乘法的结果是Tensor的每个元素乘以k（相当于把k复制成与lhs大小相同，元素全为k的Tensor）。

>>> a = torch.ones(3,4)
>>> a
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
>>> a * 2
tensor([[2., 2., 2., 2.],
        [2., 2., 2., 2.],
        [2., 2., 2., 2.]])

* 一维向量

Tensor与行向量做*乘法的结果是每列乘以行向量对应列的值（相当于把行向量的行复制）。注意此时要求Tensor的列数与行向量的列数相等。

>>> a = torch.ones(3,4)
>>> a
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
>>> b = torch.Tensor([1,2,3,4])
>>> b
tensor([1., 2., 3., 4.])
>>> a * b
tensor([[1., 2., 3., 4.],
        [1., 2., 3., 4.],
        [1., 2., 3., 4.]])

Tensor与列向量做*乘法的结果是每行乘以列向量对应行的值（相当于把列向量的列复制，成为与lhs维度相同的Tensor）. 注意此时要求Tensor的行数与列向量的行数相等。

>>> a = torch.ones(3,4)
>>> a
tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
>>> b = torch.Tensor([1,2,3]).reshape((3,1))
>>> b
tensor([[1.],
        [2.],
        [3.]])
>>> a * b
tensor([[1., 1., 1., 1.],
        [2., 2., 2., 2.],
        [3., 3., 3., 3.]])

broadcast
点积是broadcast的。broadcast是torch的一个概念，简单理解就是在一定的规则下允许高维Tensor和低维Tensor之间的运算。broadcast的概念稍显复杂，在此不做展开，可以参考官方文档关于broadcast的介绍.。
这里举一个点积broadcast的例子。在例子中，a是二维Tensor，b是三维Tensor，但是a的维度与b的后两位相同，那么a和b仍然可以做点积，点积结果是一个和b维度一样的三维Tensor，运算规则是：若c = a * b, 则c[i,*,*] = a * b[i, *, *]，即沿着b的第0维做二维Tensor点积，或者可以理解为运算前将a沿着b的第0维也进行了expand操作，即a = a.expand(b.size()); a * b。

对应点相乘，torch.mul(x, y) ，即点乘操作，点乘不求和操作，又可以叫作Hadamard product；点乘再求和，即为卷积。用法与*乘法相同，也是element-wise的乘法，也是支持broadcast的。

>>> a = torch.Tensor([[1,2], [3,4], [5, 6]])
>>> a
tensor([[1., 2.],
        [3., 4.],
        [5., 6.]])
>>> torch.mul(a, a)
tensor([[ 1.,  4.],
        [ 9., 16.],
        [25., 36.]])
 
# a*a等价于torch.mul(a, a)

>>> a = torch.tensor([[1, 2], [2, 3]])
>>> torch.mul(a,a)
tensor([[1, 4],
        [4, 9]])


>>> a = torch.tensor([[1, 2], [2, 3]])
>>> b = torch.tensor([[[1,2],[2,3]],[[-1,-2],[-2,-3]]])
>>> torch.mul(a,b)
tensor([[[ 1,  4],
         [ 4,  9]],

        [[-1, -4],
         [-4, -9]]])

矩阵相乘，torch.mm(x, y) ，矩阵大小需满足： (i, n)x(n, j)。数学里的矩阵乘法，要求两个Tensor的维度满足矩阵乘法的要求。

>>> a
tensor([[1., 2.],
        [3., 4.],
        [5., 6.]])
>>> b = a.t()  # 转置
>>> b
tensor([[1., 3., 5.],
        [2., 4., 6.]])
 
>>> torch.mm(a, b)
tensor([[ 5., 11., 17.],
        [11., 25., 39.],

1. 二维矩阵乘法 torch.mm()

torch.mm(mat1, mat2, out=None)

该函数一般只用来计算两个二维矩阵的矩阵乘法，并且不支持broadcast操作。

2. 三维带batch的矩阵乘法 torch.bmm()

由于神经网络训练一般采用mini-batch，经常输入的时三维带batch的矩阵，所以提供

torch.bmm(bmat1, bmat2, out=None)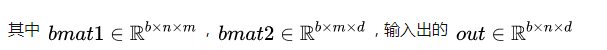

该函数的两个输入必须是三维矩阵并且第一维相同（表示Batch维度），不支持broadcast操作

3. 多维矩阵乘法 torch.matmul() torch.mm的broadcast版本.

torch.matmul(input, other, out=None)

>>> a = torch.ones(3,4)
>>> b = torch.ones(5,4,2)
>>> torch.matmul(a, b)
tensor([[[4., 4.],
         [4., 4.],
         [4., 4.]],

        [[4., 4.],
         [4., 4.],
         [4., 4.]],

        [[4., 4.],
         [4., 4.],
         [4., 4.]],

        [[4., 4.],
         [4., 4.],
         [4., 4.]],

        [[4., 4.],
         [4., 4.],
         [4., 4.]]])

支持broadcast操作，使用起来比较复杂。针对多维数据 matmul() 乘法，可以认为该乘法使用使用两个参数的后两个维度来计算，其他的维度都可以认为是batch维度。假设两个输入的维度分别是input(1000×500×99×111000×500×99×11), other(500×11×99500×11×99)那么我们可以认为torch.matmul(input, other, out=None)乘法首先是进行后两位矩阵乘法得到(99×11)×(11×99)⇒(99×99)(99×11)×(11×99)⇒(99×99) ，然后分析两个参数的batch size分别是 (1000×500)(1000×500) 和 500500 , 可以广播成为 (1000×500)(1000×500)，因此最终输出的维度是(1000×500×99×991000×500×99×99)。

4. 矩阵逐元素(Element-wise)乘法 torch.mul()

torch.mul(mat1, other, out=None)

其中 other 乘数可以是标量，也可以是任意维度的矩阵，只要满足最终相乘是可以broadcast的即可。

5. torch.einsum()