C++实现二叉树的创建及遍历
二叉树的结点类
class Node
{
public:
Node() = default;
Node(int data) : _data(data), _lchild(nullptr), _rchild(nullptr) {};
public:
char _data; // 数据域以 char 型为例,严谨点可写成模板
Node* _lchild; // 指向左孩的指针(左右孩也是一个Node)
Node* _rchild; // 指向右孩
};二叉树的建立
// 递归建立二叉树,但是这个建完了 T 就不指向根节点了,暂未解决 // 已解决,void CreatBT(Node* T) ---> void CreatBT(Node* &t); 但是为什么这样可行还需要思考一下!!!
// 这里用引用传递的方式,目的是保留原有的根节点指针指向不受影响
void CreatBT(Node* &root)
{
char ch;
cout << "请输入结点中存放的数据:";
cin >> ch;
if(ch == '#')
{
root = nullptr;
}
else
{
root = new(Node);
root->_data = ch;
CreatBT(root->_lchild);
CreatBT(root->_rchild);
}
}先序遍历二叉树
// 先序遍历二叉树
void preOrderTraverse(Node* root)
{
if(root == nullptr) {}
else
{
cout << root->_data << " ";
preOrderTraverse(root->_lchild); //递归
preOrderTraverse(root->_rchild);
}
}中序遍历二叉树
// 中序遍历二叉树
void inOrderTraverse(Node* root)
{
if(root == nullptr) {}
else
{
inOrderTraverse(root->_lchild);
cout << root->_data << " ";
inOrderTraverse(root->_rchild);
}
}
后序遍历二叉树
// 后序遍历二叉树
void postOrderTraverse(Node* root)
{
if(root == nullptr) {}
else
{
postOrderTraverse(root->_lchild);
postOrderTraverse(root->_rchild);
cout << root->_data << " ";
}
}中序遍历的非递归算法
// 中序遍历的非递归算法
void inOrdrtTraverse_norecursion(Node* root)
{
Node* p = root;
stack<Node*> s; // 使用一个栈,保存每个小二叉树的根节点
while(p != nullptr || !s.empty())
{
if(p != nullptr)
{
s.push(p);
p = p->_lchild;
}
else
{
Node* q = s.top();
s.pop();
cout << q->_data << " ";
p = q->_rchild;
}
}
}二叉树的层次遍历
// 二叉树的层次遍历
void LevelOrder(Node* root)
{
Node* p;
queue<Node*> q; // 使用一个队列,根节点入队
q.push(root);
while(!q.empty())
{
p = q.front();
cout << p->_data << " ";
q.pop();
if(p->_lchild != nullptr)
{
q.push(p->_lchild);
}
if(p->_rchild != nullptr)
{
q.push(p->_rchild);
}
}
}计算二叉树的深度
// 计算二叉树的深度
int Depth(Node* T)
{
if(T == nullptr)
{
return 0;
}
else
{
int m = Depth(T->_lchild);
int n = Depth(T->_rchild);
return (m > n) ? (m + 1) : (n + 1);
}
}计算二叉树的总结点数
// 计算二叉树结点总数
int NodeCount(Node* T)
{
if(T == nullptr)
{
return 0;
}
else
{
return NodeCount(T->_lchild) + NodeCount(T->_rchild) + 1;
}
}计算二叉树叶子节点数
// 计算二叉树叶子节点数
int leafNodeCount(Node* T)
{
if(T == nullptr)
{
return 0;
}
if(T->_lchild == nullptr && T->_rchild == nullptr)
{
return 1;
}
else
{
return leafNodeCount(T->_lchild) + leafNodeCount(T->_rchild);
}
}测试
构建如下测试用例二叉树,并依次测试所写的每一个函数。
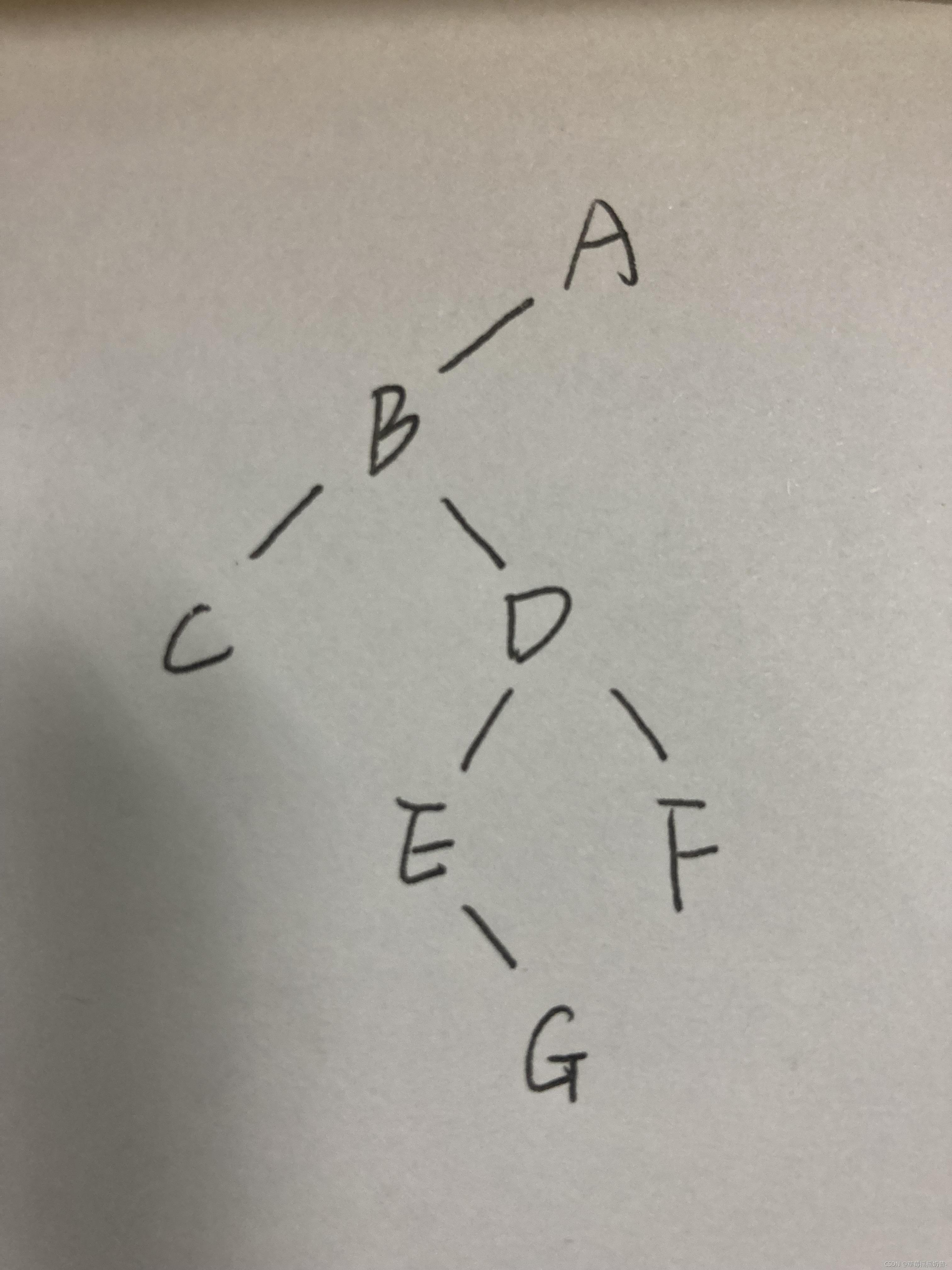
按照二叉树的建立函数中的思路,将其以 ‘#’ 补齐为满二叉树,如下 :
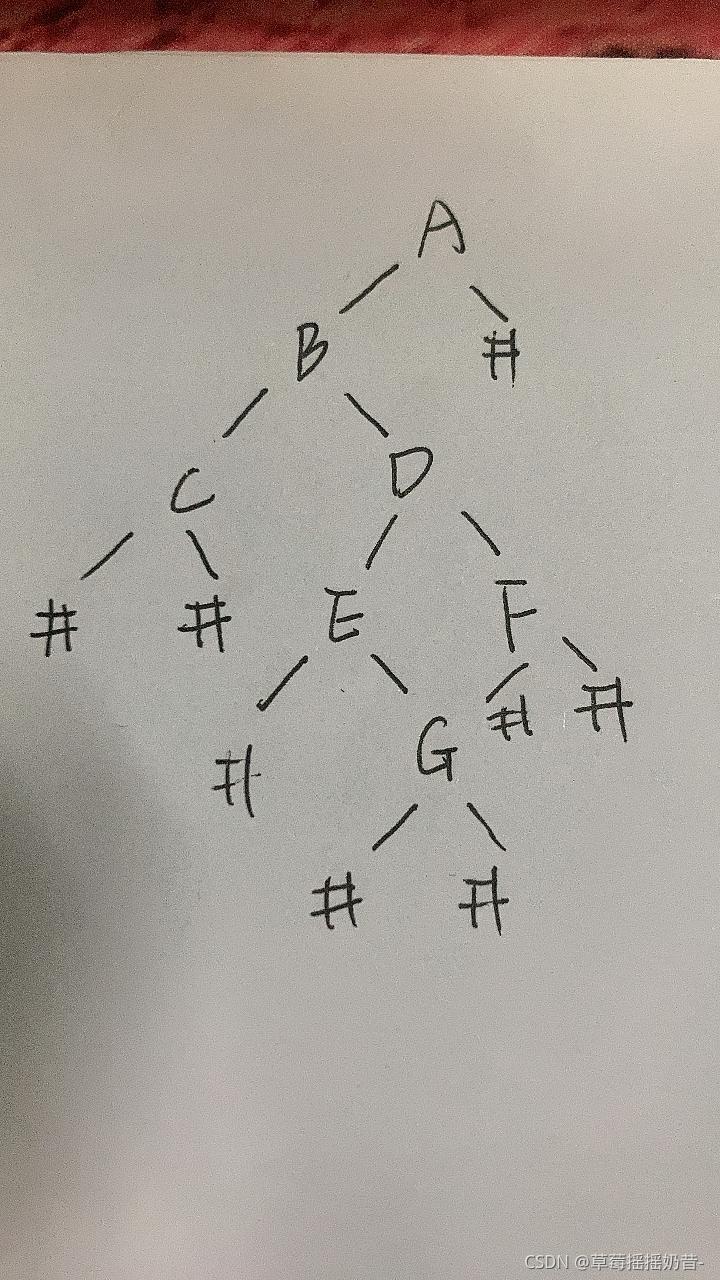
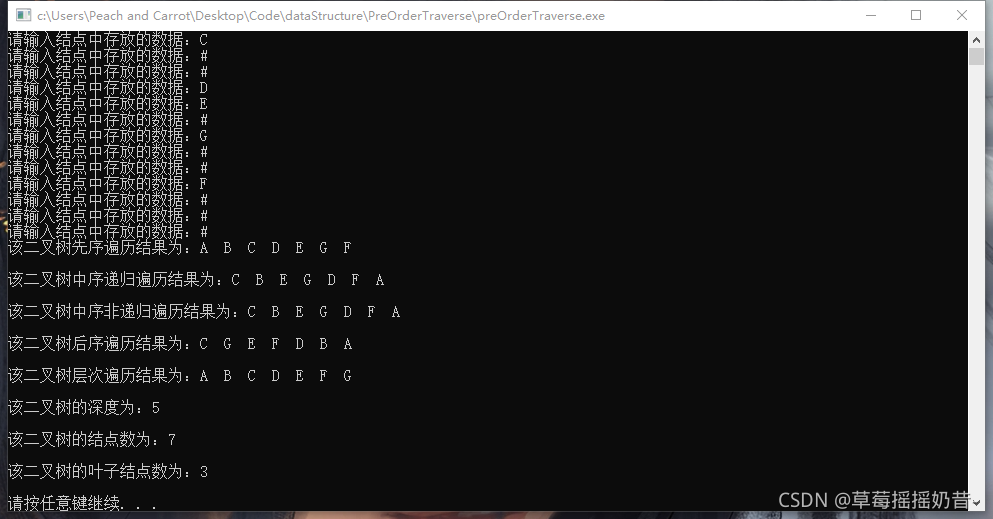
其先序遍历为:ABC##DE#G##F###,我们按照这个顺序建立二叉树,并进行测试,结果如下:
完整代码
#include <iostream>
#include <stack>
#include <queue>
#include <string>
using namespace std;
// 二叉链树的创建和遍历
class Node
{
public:
Node() = default;
Node(int data) : _data(data), _lchild(nullptr), _rchild(nullptr) {};
public:
char _data; // 数据域以 char 型为例,严谨点可写成模板
Node* _lchild; // 指向左孩的指针(左右孩也是一个Node)
Node* _rchild; // 指向右孩
};
// 递归建立二叉树,但是这个建完了 T 就不指向根节点了,暂未解决 // 已解决,void CreatBT(Node* T) ---> void CreatBT(Node* &t); 但是为什么这样可行还需要思考一下!!!
// 这里用引用传递的方式,目的是保留原有的根节点指针指向不受影响
void CreatBT(Node* &root)
{
char ch;
cout << "请输入结点中存放的数据:";
cin >> ch;
if(ch == '#')
{
root = nullptr;
}
else
{
root = new(Node);
root->_data = ch;
CreatBT(root->_lchild);
CreatBT(root->_rchild);
}
}
// 先序遍历二叉树
void preOrderTraverse(Node* root)
{
if(root == nullptr) {}
else
{
cout << root->_data << " ";
preOrderTraverse(root->_lchild); //递归
preOrderTraverse(root->_rchild);
}
}
// 中序遍历二叉树
void inOrderTraverse(Node* root)
{
if(root == nullptr) {}
else
{
inOrderTraverse(root->_lchild);
cout << root->_data << " ";
inOrderTraverse(root->_rchild);
}
}
// 后序遍历二叉树
void postOrderTraverse(Node* root)
{
if(root == nullptr) {}
else
{
postOrderTraverse(root->_lchild);
postOrderTraverse(root->_rchild);
cout << root->_data << " ";
}
}
// 中序遍历的非递归算法
void inOrdrtTraverse_norecursion(Node* root)
{
Node* p = root;
stack<Node*> s; // 使用一个栈,保存每个小二叉树的根节点
while(p != nullptr || !s.empty())
{
if(p != nullptr)
{
s.push(p);
p = p->_lchild;
}
else
{
Node* q = s.top();
s.pop();
cout << q->_data << " ";
p = q->_rchild;
}
}
}
// 二叉树的层次遍历
void LevelOrder(Node* root)
{
Node* p;
queue<Node*> q; // 使用一个队列,根节点入队
q.push(root);
while(!q.empty())
{
p = q.front();
cout << p->_data << " ";
q.pop();
if(p->_lchild != nullptr)
{
q.push(p->_lchild);
}
if(p->_rchild != nullptr)
{
q.push(p->_rchild);
}
}
}
// 计算二叉树的深度
int Depth(Node* T)
{
if(T == nullptr)
{
return 0;
}
else
{
int m = Depth(T->_lchild);
int n = Depth(T->_rchild);
return (m > n) ? (m + 1) : (n + 1);
}
}
// 计算二叉树结点总数
int NodeCount(Node* T)
{
if(T == nullptr)
{
return 0;
}
else
{
return NodeCount(T->_lchild) + NodeCount(T->_rchild) + 1;
}
}
// 计算二叉树叶子节点数
int leafNodeCount(Node* T)
{
if(T == nullptr)
{
return 0;
}
if(T->_lchild == nullptr && T->_rchild == nullptr)
{
return 1;
}
else
{
return leafNodeCount(T->_lchild) + leafNodeCount(T->_rchild);
}
}
void test01()
{
Node* T = nullptr;
CreatBT(T);
cout << "该二叉树先序遍历结果为:";
preOrderTraverse(T);
cout << endl << endl;
cout << "该二叉树中序递归遍历结果为:";
inOrderTraverse(T);
cout << endl << endl;
cout << "该二叉树中序非递归遍历结果为:";
inOrdrtTraverse_norecursion(T);
cout << endl << endl;
cout << "该二叉树后序遍历结果为:";
postOrderTraverse(T);
cout << endl << endl;
cout << "该二叉树层次遍历结果为:";
LevelOrder(T);
cout << endl << endl;
cout << "该二叉树的深度为:" << Depth(T) << endl << endl;
cout << "该二叉树的结点数为:" << NodeCount(T) << endl << endl;
cout << "该二叉树的叶子结点数为:" << leafNodeCount(T) << endl << endl;
}
int main()
{
test01();
system("pause");
return 0;
}