布隆过滤器定义长度为m的数组,插入n个元素,k个哈希函数,已知m和n的值,k的值为多少时,求误判率最低的推导过程?
布隆过滤器是怎么存储数据的?
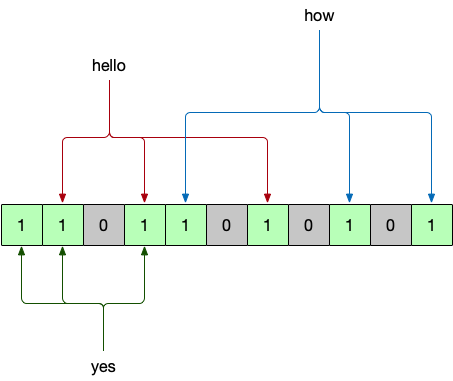
这里m=11,数组长度为11,n=3,插入3个元素,分别是hello、how、yes,k=3,使用了3个哈希函数,每插入一个元素要经过三个哈希函数的运算。
①插入hello元素,需要经过3个哈希函数,得出3个不同的哈希值索引【1,3,6】,那么在1,3,6的位置设置为1。
②插入how元素,需要经过3个哈希函数,得出3个不同的哈希索引值【4,8,10】,那么在4,8,10的位置设置为1。
③插入yes元素,需要经过3个哈希函数,得出3个不同的哈希值索引值【0,1,3】,那么在0,1,3的位置设置为1。
④误判的情况:判断ok元素是否存在?ok这个元素经过3个哈希函数运算以后,得出的索引值也是【0,1,3】,这个索引值和yes元素是一样的,然而布隆过滤器认为ok这个元素是存在的,但实际上不存在的,因为哈希值冲突了。
设布隆过滤器的长度为m,插入n个素,进行k个哈希函数运算,已知m和n的值,问:当k的值为多少的时候,误判率最低?
解:
长度为m,插入1个元素,1个哈希函数运算的情况下,某一位是1的概率为: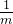 ,那么某一位为0的概率就是
,那么某一位为0的概率就是 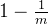
长度为m,插入n个元素,1个哈希函数运算的情况下,一次插入1个元素(每次插入的元素可能有某几次是重复的),插入n次,相当于插入了n个元素,插入这么多次以后,某一位仍然为0的概率是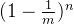
长度为m,插入n个元素,每插入一个元素之前就经过k个哈希函数运算的情况下,一次插入1个元素,插入n次,相当于插入了n个元素,插入这么多次以后,某一位仍然为0的概率是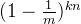
反过来,某一位为1的概率就是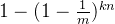
那么,某两位同时为1的概率就是![[1-(1-\frac{1}{m})^{kn}]^{2}](https://images2.imgbox.com/ea/6e/lhl9OMsg_o.png) ,某三位同时为1的概率就是
,某三位同时为1的概率就是![[1-(1-\frac{1}{m})^{kn}]^{3}](https://images2.imgbox.com/6e/60/JnKr8joE_o.png) ,某k位同时为1的概率就是
,某k位同时为1的概率就是![[1-(1-\frac{1}{m})^{kn}]^{k}](https://images2.imgbox.com/bf/cc/NoRVO1Qt_o.png) ,这个概率,就是误判率,因为检查是否有某个元素的时候,某k位同时为1,说明有这个元素,但这个元素是外来的,本身不存在于集合当中。
,这个概率,就是误判率,因为检查是否有某个元素的时候,某k位同时为1,说明有这个元素,但这个元素是外来的,本身不存在于集合当中。
误判率 ![f(k) = [1-(1-\frac{1}{m})^{kn}]^{k}](https://images2.imgbox.com/10/71/RKbpc9zK_o.png) ,其中m,n都是常数,求这个函数是最小值的时候,k等于多少?
,其中m,n都是常数,求这个函数是最小值的时候,k等于多少?
当m足够大的时候,也就是数组足够长的时候,能够确保误判率足够,此时,把式子变形:
![f(k) = [1 - (1 - \frac{1}{m})^{-m\cdot \frac{-kn}{m}}]^{k}](https://images2.imgbox.com/a3/a3/1sFj26SH_o.png)
因为m是一个很大的数字,可能是100万,1000万这个数量级别的,足以让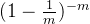 趋近于 e
趋近于 e
所以,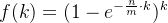
两边都取ln对数得:
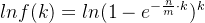 ,即
,即 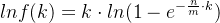
令 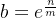 ,那么
,那么 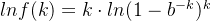
两边求导:
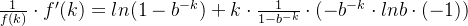
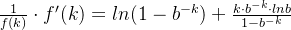
因为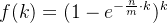 ,且
,且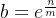 ,所以
,所以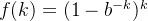
式子两边同时乘以f(k)得到:
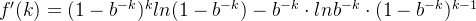
再令 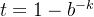
所以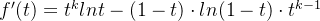
提出一个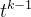
![{f'(t)} = t^{k-1}[tlnt - (1-t)ln(1-t)]](https://images2.imgbox.com/f1/e2/DzWZJazI_o.png)
因为k是大于等于1的整数,b是大于1的数字,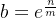 ,那么
,那么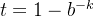 ,t的取值范围就是(0,1)
,t的取值范围就是(0,1)
那么研究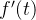 在(0,1)的区间里面的正负性,我们发现当t=1/2 的时候,
在(0,1)的区间里面的正负性,我们发现当t=1/2 的时候,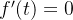 ,那么,咱们就来研究,这个导函数在区间
,那么,咱们就来研究,这个导函数在区间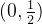 和区间
和区间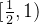 的正负性。
的正负性。
在研究正负性之前,咱们要先研究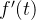 的极限和增减性。
的极限和增减性。
首先来看极限:
研究函数 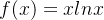 和函数
和函数 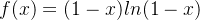 的极限,因为函数
的极限,因为函数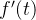 包含了这两种函数,所以咱们要研究它
包含了这两种函数,所以咱们要研究它
当x -> 0+ 的时候,使用洛必达法则:
对函数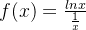 的分子
的分子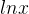 以及分母
以及分母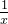 分别求导,得到分子是
分别求导,得到分子是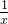 ,分母是
,分母是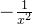 ,这时候,分别在分子和分母同时乘以
,这时候,分别在分子和分母同时乘以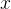 ,得到
,得到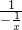 ,即
,即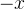 ,当x->0+ 的时候,
,当x->0+ 的时候,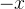 是趋近于0- 的,所以当x->0+ 的时候,函数
是趋近于0- 的,所以当x->0+ 的时候,函数 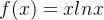 也是无限趋近于0的,并且是负数。
也是无限趋近于0的,并且是负数。
x->0+ 的时候 ,函数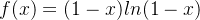 ,
,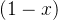 是无穷趋近于1的且小于1,
是无穷趋近于1的且小于1,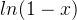 是无穷趋近于0的,并且小于0,那么这两个数不是0/0或者∞/∞形式的,就不适用于洛必达法则去求极限了,直接得出极限是函数
是无穷趋近于0的,并且小于0,那么这两个数不是0/0或者∞/∞形式的,就不适用于洛必达法则去求极限了,直接得出极限是函数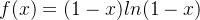 无穷趋近于0,并且小于0,一个有限的数乘以一个无穷趋近于0的负数,结果肯定是无穷趋近于0。
无穷趋近于0,并且小于0,一个有限的数乘以一个无穷趋近于0的负数,结果肯定是无穷趋近于0。
那么这时候当t->0+ 的时候,![{f'(t)} = t^{k-1}[tlnt - (1-t)ln(1-t)]](https://images2.imgbox.com/16/81/kFTwPYBd_o.png) ,
, 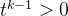 不用说,咱们只要能够画出函数
不用说,咱们只要能够画出函数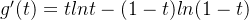 的图像,判断函数
的图像,判断函数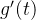 在区间(0,1)的正负性即可。
在区间(0,1)的正负性即可。
函数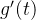 确认了3个点:
确认了3个点:
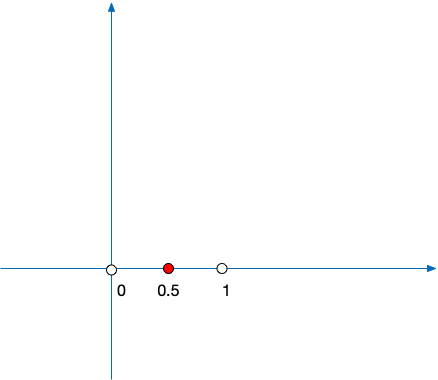
函数图像是怎么经过这3个点的呢?(0,0)和(1,0)是无限趋近的点。
再次对函数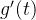 求导:
求导:
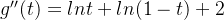
我们通过工具,发现,这个导函数的图像是这样的:
在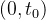 的区间,
的区间,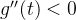 ,
,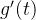 是单调递减的,
是单调递减的,
在区间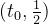 ,
,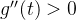 ,
,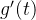 是单调递增的,
是单调递增的,
在区间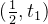 ,
,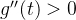 ,
,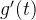 是单调递增的,
是单调递增的,
在区间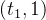 ,
, 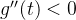 ,
,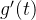 是单调递减的
是单调递减的
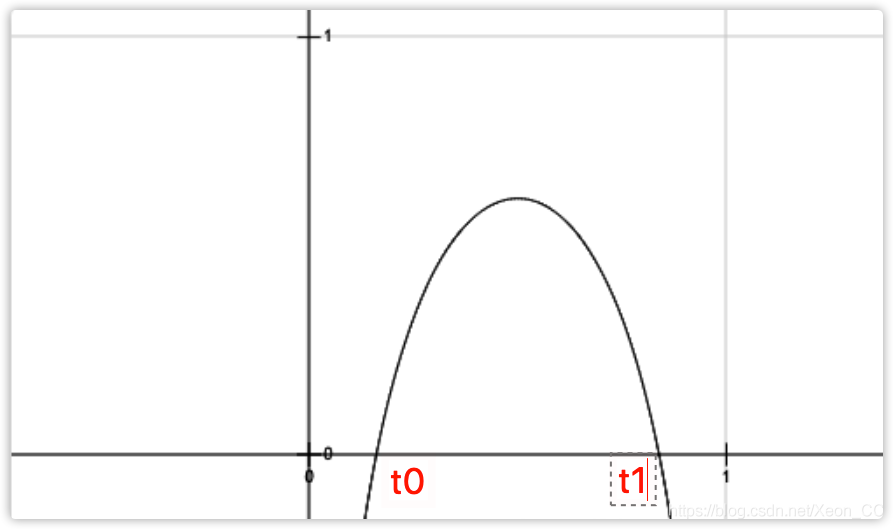
知道函数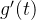 经过了
经过了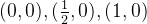 这三个点,(不包括(0,0)和(1,0),只能无穷趋近这两个点),也知道在某些区间的增减性了。
这三个点,(不包括(0,0)和(1,0),只能无穷趋近这两个点),也知道在某些区间的增减性了。
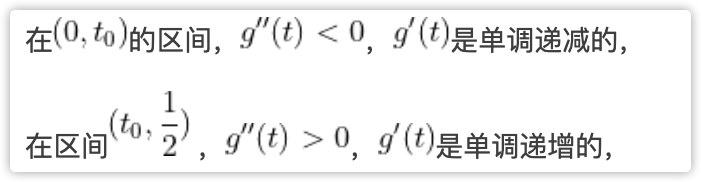
那么在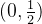 区间,一定是先减后增的,图像必须这么画:
区间,一定是先减后增的,图像必须这么画:
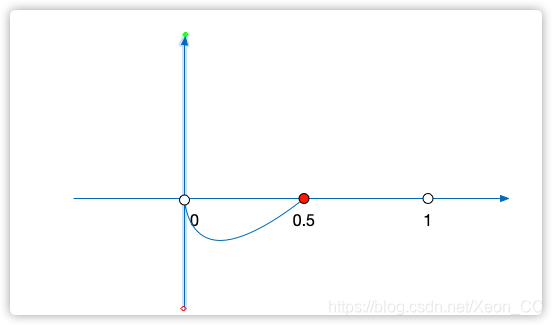
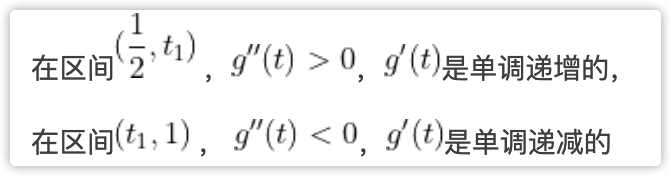
那么在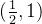 区间,必须是先增后减的,图像必须这么画:
区间,必须是先增后减的,图像必须这么画:
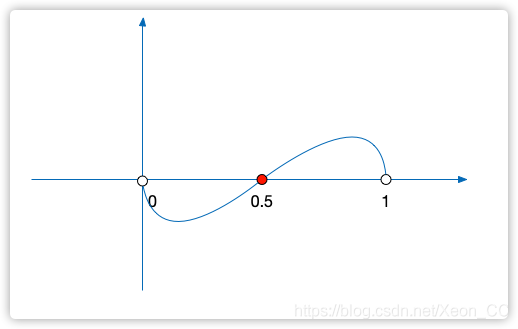
可见函数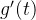 在
在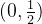 区间,
区间,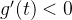 则
则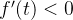 ,
,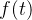 单调递减,函数
单调递减,函数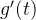 在
在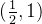 区间,
区间,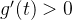 ,则
,则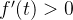 ,
,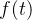 单调递增,当
单调递增,当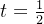 时,
时,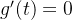 ,则
,则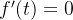
那么,当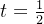 时候,误判率
时候,误判率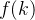 取得最小值,由于
取得最小值,由于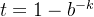 ,
,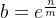
得出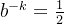 ,
,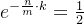
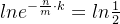
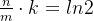
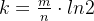
当知道数组长度m和插入数据量为n的时候,最优的哈希函数个数 k 为 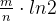 个,(k属于正整数)
个,(k属于正整数)