线性/非线性规划问题求解

1、用Excel求解线性规划问题

一般购买的电脑都已经安装好了Microsoft Office，就不需要进行下载安装这一过程。

一、使用Excel做线性回归

1.添加数据分析的工具

如果选择数据后，在工具栏中有数据分析的选择，设置过程可以忽略。

①选择文件
在这里插入图片描述
②选择选项

③首先选择加载项，接着将管理处修改为Excel加载项，最后选择转到

④分析工具库和分析工具库-VBA勾选上，接着选择确定

⑤查看是否添加完成，如下图所示，表示添加成功

2.Excel完成线性回归分析
①打开需要进行分析的数据文件
②选择数据->数据分析->回归->确定
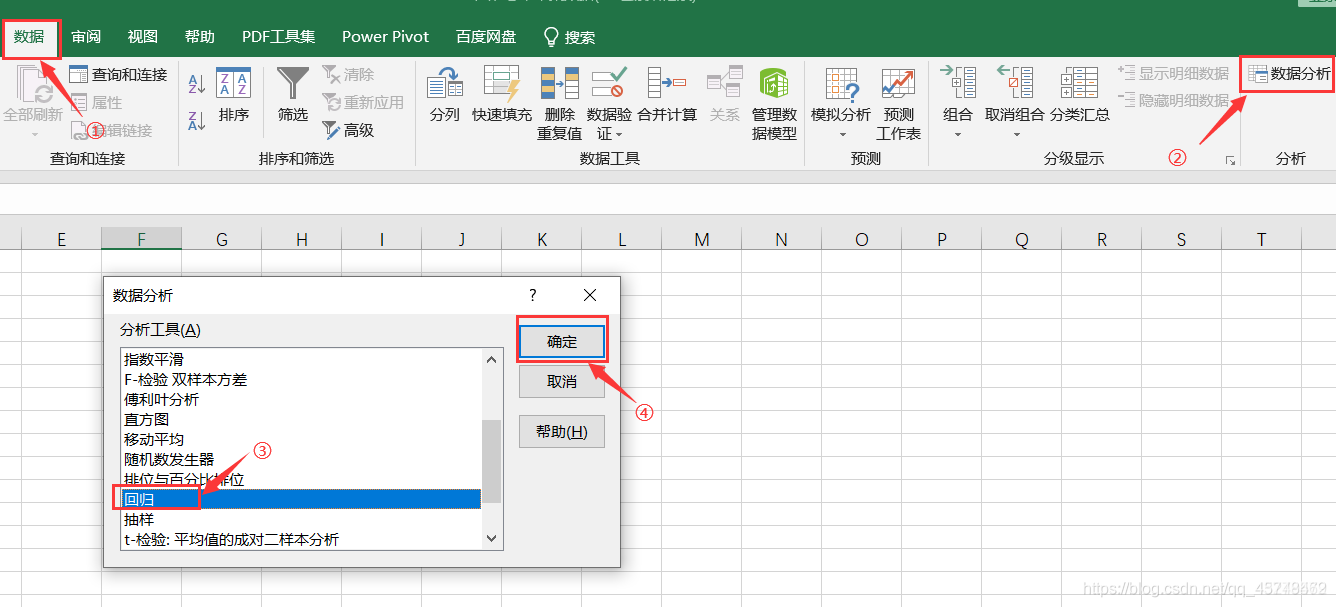
在这里插入图片描述
③进行相关设置

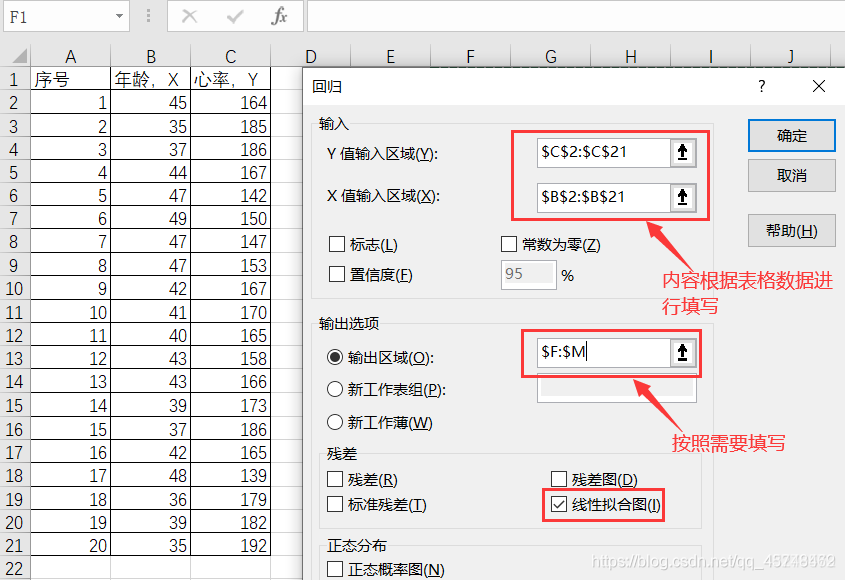
输出图表如下

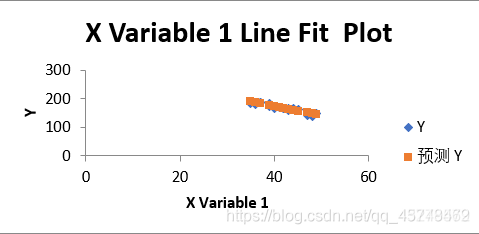
默认生成的图表显示不是很好看，进行一些相关设置，使其显示更具清楚具体

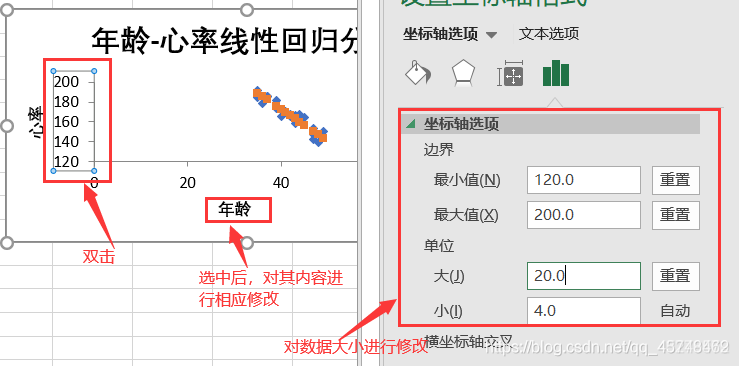
修改后如下图所示

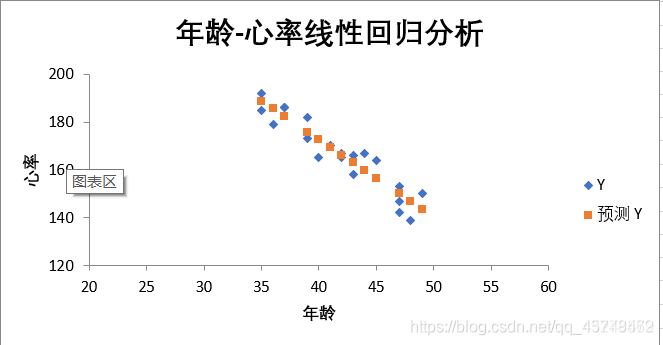
④选中原始数据，点击右键，选择添加趋势线

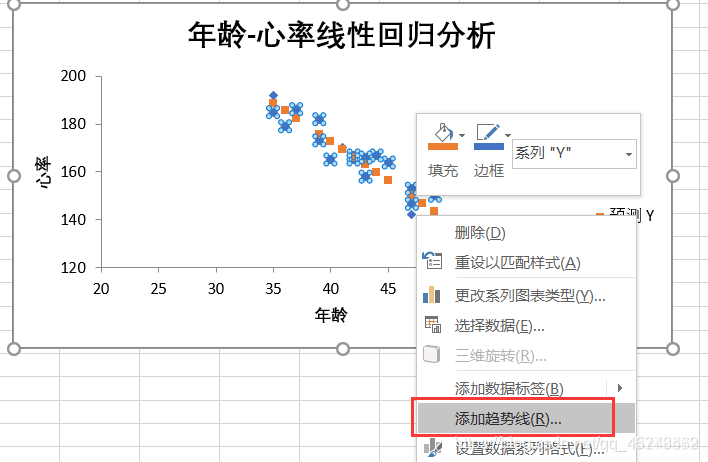
趋势线的格式设置：选择线性，勾选显示公式（其他更多设置根据需要进行选择）
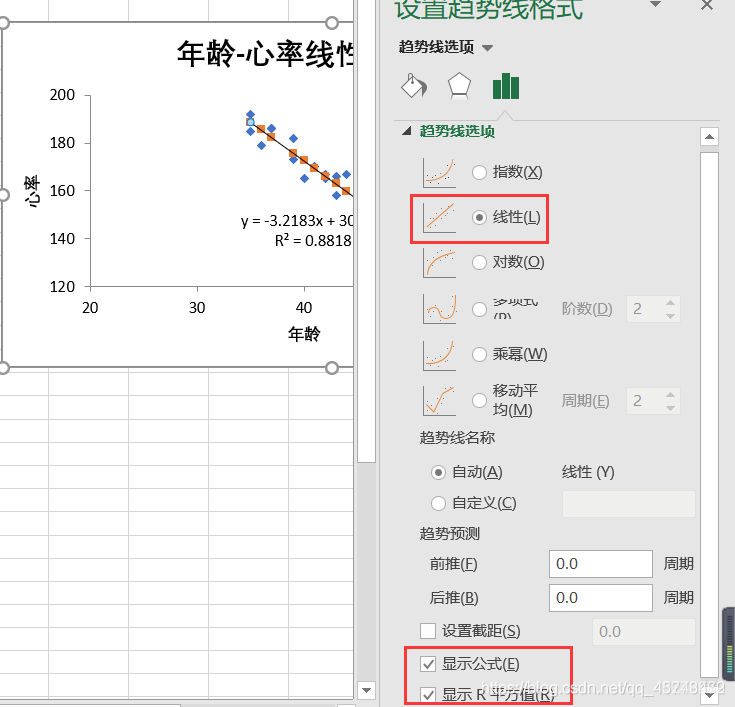
在这里插入图片描述
最终效果图如下

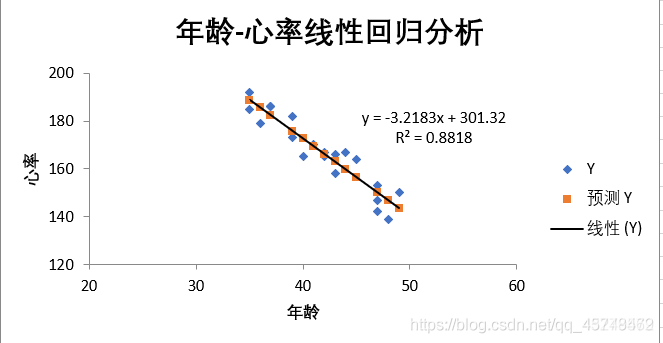
对于其他数据进行线性回归分析操作过程一样。

二、验证回归方程的精度

1.R值
在统计学中R值是拟合优度指数,用来评价模型的拟合好坏等,取值范围是【-1,1】,越接近正负1越好。对应R平方来说越接近1越好。
R值的大小
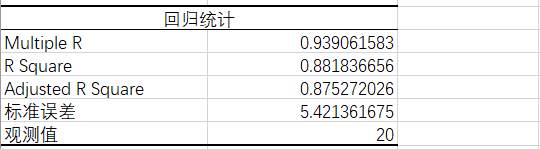
在这里插入图片描述
通过数据分析可以计算出R平方的取值约为0.88，表明该模型的拟合程度还是比较好的。
2.P值
在统计学中P值是指（F检验或者T或者其余检验量）大于所求值时的概率,一般要小于给定α就说明检验显著。P值是检验样置信度的一个指标，一般我们认为p<=0.05时(一般选择这个显著水平)，模型的信号不存在偶然性，模型的结果可靠。
P值的大小
在这里插入图片描述
通过数据分析可以看出P值远远小于0.05，表面得到的回归方程是可靠的。

说明：一般通过R和P值的大小来判断一个模型是否是合适和可靠的。

2、拉格朗日求解最优问题——条件极值

一、问题

在这里插入图片描述

二、拉格朗日手工求解

在这里插入图片描述
2、偏导解变量

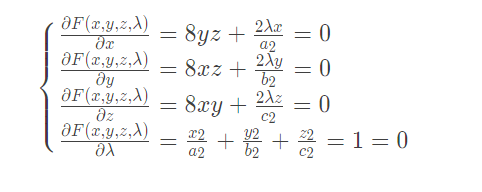
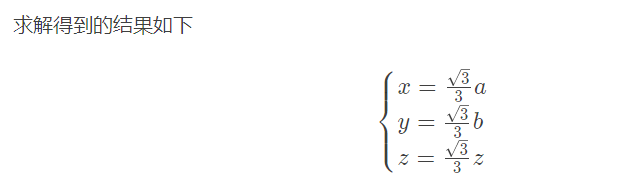
3、带入

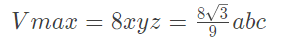
三、拉格朗日编程求解

代码实现

# 导入包
from sympy import *
# 设置变量
x,y,z,k = symbols('x,y,z,k')
a,b,c=symbols('a,b,c')
f = 8*x*y*z
g = x**2/a**2+y**2/b**2+z**2/c**2-1
#构造拉格朗日函数
L=f+k*g
#求导
dx = diff(L, x)   # 对x求偏导
print("dx=",dx)
dy = diff(L,y)   #对y求偏导
print("dy=",dy)
dz = diff(L,z)   #对z求偏导
print("dz=",dz)
dk = diff(L,k)   #对k求偏导
print("dk=",dk)
dx= 8*y*z + 2*k*x/a**2
dy= 8*x*z + 2*k*y/b**2
dz= 8*x*y + 2*k*z/c**2
dk= -1 + z**2/c**2 + y**2/b**2 + x**2/a**2
#求出个变量解
m= solve([dx,dy,dz,dk],[x,y,z,k])   
print(m)
#变量赋值
x=sqrt(3)*a/3
y=sqrt(3)*b/3
z=sqrt(3)*c/3
k=-4*sqrt(3)*a*b*c/3
#计算方程的值
f = 8*x*y*z
print("方程的最大值为：",f)

通过diff函数求解的偏导

通过solve函数求解变量

最终求解结果
在这里插入图片描述

参考链接

怎么用excel做线性回归分析
 https://blog.csdn.net/xianyudewo/article/details/115379483
https://blog.csdn.net/qq_43279579/article/details/114375204

目录