2021ICPC上海区域赛DEGKI
题目链接:
https://codeforces.com/gym/103446
视频讲解:
https://www.bilibili.com/video/bv1994y1f76o
代码:https://hytidel.lanzoub.com/b030vuwli
密码:fkgp
2021ICPC上海区域赛题解DEGIK
E. Strange Integers
题意
给定 n ( 1 ≤ n ≤ 1 e 5 ) n\ \ (1\leq n\leq 1\mathrm{e}5) n (1≤n≤1e5)个数 a 1 , ⋯ , a n ( 1 ≤ a i ≤ 1 e 9 ) a_1,\cdots,a_n\ \ (1\leq a_i\leq 1\mathrm{e}9) a1,⋯,an (1≤ai≤1e9)和一个参数 k ( 0 ≤ k ≤ 1 e 9 ) k\ \ (0\leq k\leq 1\mathrm{e}9) k (0≤k≤1e9),问从中至多可以选出几个数使得选出来的数两两之差的绝对值不小于 k k k.
解I
n n n最大 1 e 5 1\mathrm{e}5 1e5,时间 1 s 1\ s 1 s,考虑 O ( n ) O(n) O(n)暴力枚举.将序列升序排列后取出最大数 m a x n u m maxnum maxnum,从后往前扫一遍序列,每次检查两数之差是否 ≥ k \geq k ≥k,若是则 a n s + + ans++ ans++,并将 m a x n u m maxnum maxnum更新为当前的 a [ i ] a[i] a[i].
代码I -> 2021ICPC上海-E(暴力)
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<unordered_set>
#include<unordered_map>
#include<sstream>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
typedef queue<int> qi;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, double> pdd;
#define umap unordered_map
#define IOS ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
#define CaseT int CaseT; cin >> CaseT; while(CaseT--)
#define endl '\n'
#define so sizeof
#define pb push_back
#define npt nullptr
const double eps = 1e-7;
const int INF = 0x3f3f3f3f;
const ll INFF = 0x3f3f3f3f3f3f3f3f;
const int MAXN = 1e5 + 5;
int n, k; // 元素个数、参数
int nums[MAXN];
int minnum = INF;
int ans = 1; // 至少选最小数
int main() {
IOS;
#ifndef ONLINE_JUDGE
clock_t my_clock = clock();
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
// ----------------------------------------------------------------
cin >> n >> k;
for (int i = 0; i < n; i++) cin >> nums[i];
sort(nums, nums + n);
int maxnum = nums[n - 1];
for (int i = n - 2; i >= 0; i--) {
if (maxnum - nums[i] >= k) {
ans++;
maxnum = nums[i];
}
}
cout << ans;
// ----------------------------------------------------------------
#ifndef ONLINE_JUDGE
cout << endl << "Time used " << clock() - my_clock << " ms." << endl;
#endif
return 0;
}
解II
贪心.将序列升序排列后取出最小数 m i n n u m minnum minnum,每次取序列中第一个 ≥ m i n n u m + k \geq minnum+k ≥minnum+k的数,直至无法再取或已取完整个序列.
代码II -> 2021ICPC上海-E(贪心+lower_bound或二分)
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<unordered_set>
#include<unordered_map>
#include<sstream>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
typedef queue<int> qi;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, double> pdd;
#define umap unordered_map
#define IOS ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
#define CaseT int CaseT; cin >> CaseT; while(CaseT--)
#define endl '\n'
#define so sizeof
#define pb push_back
#define npt nullptr
const double eps = 1e-7;
const int INF = 0x3f3f3f3f;
const ll INFF = 0x3f3f3f3f3f3f3f3f;
const int MAXN = 1e5 + 5;
int n, k; // 元素个数、参数
int nums[MAXN];
int minnum = INF;
int ans = 1; // 至少选最小数
int main() {
IOS;
#ifndef ONLINE_JUDGE
clock_t my_clock = clock();
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
// ----------------------------------------------------------------
cin >> n >> k;
for (int i = 0; i < n; i++) {
cin >> nums[i];
minnum = min(minnum, nums[i]);
}
sort(nums, nums + n);
int idx = lower_bound(nums, nums + n, minnum + k) - nums;
while (idx != n) {
ans++;
minnum = nums[idx];
idx = lower_bound(nums, nums + n, minnum + k) - nums;
}
cout << ans;
// ----------------------------------------------------------------
#ifndef ONLINE_JUDGE
cout << endl << "Time used " << clock() - my_clock << " ms." << endl;
#endif
return 0;
}
但事实上,暴力解法比lower_bound的解法还快,如下图,上面是暴力,下面是lower_bound.

D. Strange Fractions
题意
给定 T ( 1 ≤ T ≤ 1 e 5 ) T\ \ (1\leq T\leq 1\mathrm{e}5) T (1≤T≤1e5)个分数 p q ( 1 ≤ p , q ≤ 1 e 7 ) \dfrac{p}{q}\ \ (1\leq p,q\leq 1\mathrm{e}7) qp (1≤p,q≤1e7),求整数 a , b ( 1 ≤ a , b ≤ 1 e 9 ) s . t . p q = a b + b a a,b\ \ (1\leq a,b\leq 1\mathrm{e}9)\ s.t.\ \dfrac{p}{q}=\dfrac{a}{b}+\dfrac{b}{a} a,b (1≤a,b≤1e9) s.t. qp=ba+ab,若不存在,输出 0 0 0\ 0 0 0.
注
只需讨论 p q \dfrac{p}{q} qp是最简分式的情况,若不然,分子分母同除以 gcd ( p , q ) \gcd(p,q) gcd(p,q)化为最简分式. p q = a b + b a = a 2 + b 2 a b \dfrac{p}{q}=\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{a^2+b^2}{ab} qp=ba+ab=aba2+b2,注意这里推不出 { p = a 2 + b 2 q = a b \begin{cases}p=a^2+b^2 \\ q=ab\end{cases} {p=a2+b2q=ab,因 a 2 + b 2 a^2+b^2 a2+b2与 a b ab ab未必互素,如 a = b = 2 a=b=2 a=b=2时, a 2 + b 2 a b = 8 4 \dfrac{a^2+b^2}{ab}=\dfrac{8}{4} aba2+b2=48,而 p = 2 , q = 1 p=2,q=1 p=2,q=1.
但是有题解这样推导,最后还是AC了,这是因为它忽略了指向正解的一步,见解II.
解I
令 x = a b , k = p q x=\dfrac{a}{b},k=\dfrac{p}{q} x=ba,k=qp,化为关于 x x x的一元二次方程 x 2 − k x + 1 = 0 x^2-kx+1=0 x2−kx+1=0,其判别式 Δ = k 2 − 4 \Delta=k^2-4 Δ=k2−4,方程有实根当且仅当 k 2 − 4 = p 2 q 2 − 4 ≥ 0 k^2-4=\dfrac{p^2}{q^2}-4\geq 0 k2−4=q2p2−4≥0,即 p 2 ≥ 4 q 2 p^2\geq 4q^2 p2≥4q2.
为使 x = k ± k 2 − 4 2 = p q ± p 2 − 4 q 2 q 2 = p ± p 2 − 4 q 2 2 q ∈ Q x=\dfrac{k\pm\sqrt{k^2-4}}{2}=\dfrac{\dfrac{p}{q}\pm\dfrac{\sqrt{p^2-4q^2}}{q}}{2}=\dfrac{p\pm\sqrt{p^2-4q^2}}{2q}\in\mathbb{Q} x=2k±k2−4=2qp±qp2−4q2=2qp±p2−4q2∈Q,则 p 2 − 4 q 2 ∈ Z \sqrt{p^2-4q^2}\in\mathbb{Z} p2−4q2∈Z,进而 p 2 − 4 q 2 p^2-4q^2 p2−4q2是平方数,设其平方根为 t m p tmp tmp,则 a b = p ± t m p 2 q \dfrac{a}{b}=\dfrac{p\pm tmp}{2q} ba=2qp±tmp,为保证 a , b ≥ 1 a,b\geq 1 a,b≥1,则取 a = p + t m p a=p+tmp a=p+tmp和 b = 2 q b=2q b=2q,注意将其约分再输出.未必要输出小数在前.
代码I -> 2021ICPC上海-D(推公式做法I)
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<unordered_set>
#include<unordered_map>
#include<sstream>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
typedef queue<int> qi;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, double> pdd;
#define umap unordered_map
#define IOS ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
#define CaseT int CaseT; cin >> CaseT; while(CaseT--)
#define endl '\n'
#define so sizeof
#define pb push_back
#define npt nullptr
const double eps = 1e-7;
const int INF = 0x3f3f3f3f;
const ll INFF = 0x3f3f3f3f3f3f3f3f;
int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
bool check(ll n) { // 判断n是否为平方数
ll tmp = floor(sqrt(n) + 0.5);
return tmp * tmp == n;
}
int main() {
IOS;
#ifndef ONLINE_JUDGE
clock_t my_clock = clock();
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
// ----------------------------------------------------------------
CaseT{
int p, q; cin >> p >> q;
if ((ll)p * p < (ll)4 * q * q) { // 无解
cout << "0 0" << endl;
continue;
}
ll tmp = (ll)p * p - (ll)4 * q * q; // p^2-4q^2
if (!check(tmp)) { // 无解
cout << "0 0" << endl;
continue;
}
tmp = sqrt(tmp);
int d = gcd(p + tmp, 2 * q);
cout << (p + tmp) / d << ' ' << (2 * q) / d << endl;
}
// ----------------------------------------------------------------
#ifndef ONLINE_JUDGE
cout << endl << "Time used " << clock() - my_clock << " ms." << endl;
#endif
return 0;
}
解II
只需讨论 p q \dfrac{p}{q} qp是最简分式的情况,若不然,分子分母同除以 gcd ( p , q ) \gcd(p,q) gcd(p,q)化为最简分式. p q = a b + b a = a 2 + b 2 a b \dfrac{p}{q}=\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{a^2+b^2}{ab} qp=ba+ab=aba2+b2.若约定 gcd ( a , b ) = 1 \gcd(a,b)=1 gcd(a,b)=1,则 gcd ( a 2 + b 2 , a b ) = 1 \gcd(a^2+b^2,ab)=1 gcd(a2+b2,ab)=1,进而推出 { p = a 2 + b 2 q = a b \begin{cases}p=a^2+b^2 \\ q=ab\end{cases} {p=a2+b2q=ab.
注意到 { a + b = p + 2 q a − b = p − 2 q \begin{cases}a+b=\sqrt{p+2q} \\ a-b=\sqrt{p-2q}\end{cases} {a+b=p+2qa−b=p−2q,若 p + 2 q , p − 2 q p+2q,p-2q p+2q,p−2q是平方数,则有合法的 { a = p + 2 q + p − 2 q 2 b = p + 2 q − p − 2 q 2 \begin{cases}a=\dfrac{\sqrt{p+2q}+\sqrt{p-2q}}{2} \\ b=\dfrac{\sqrt{p+2q}-\sqrt{p-2q}}{2}\end{cases} ⎩⎪⎨⎪⎧a=2p+2q+p−2qb=2p+2q−p−2q,判断 a , b a,b a,b是否为整数.
gcd ( a , b ) = 1 \gcd(a,b)=1 gcd(a,b)=1时,有 gcd ( a 2 + b 2 , a b ) = 1 \gcd(a^2+b^2,ab)=1 gcd(a2+b2,ab)=1的证明:不妨设 a = ∏ i p i α i , b = ∏ i q i β i \displaystyle a=\prod_i p_i^{\alpha_i},b=\prod_i q_i^{\beta_i} a=i∏piαi,b=i∏qiβi,其中 p i ≠ q i p_i\neq q_i pi=qi,则 a b = ( ∏ i p i α i ) ( ∏ i q i β i ) , a 2 + b 2 = ∏ i p i 2 α i + ∏ i q i 2 β i \displaystyle ab=\left(\prod_i p_i^{\alpha_i}\right)\left(\prod_i q_i^{\beta_i}\right),a^2+b^2=\prod_i p_i^{2\alpha_i}+\prod_i q_i^{2\beta_i} ab=(i∏piαi)(i∏qiβi),a2+b2=i∏pi2αi+i∏qi2βi,则显然 a 2 + b 2 a^2+b^2 a2+b2的 R H S \mathrm{RHS} RHS的两项都不能被 a b ab ab整除,故 gcd ( a 2 + b 2 , a b ) = 1 \gcd(a^2+b^2,ab)=1 gcd(a2+b2,ab)=1.
代码II -> 2021ICPC上海-D(推公式做法II)
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<unordered_set>
#include<unordered_map>
#include<sstream>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
typedef queue<int> qi;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, double> pdd;
#define umap unordered_map
#define IOS ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
#define CaseT int CaseT; cin >> CaseT; while(CaseT--)
#define endl '\n'
#define so sizeof
#define pb push_back
#define npt nullptr
const double eps = 1e-7;
const int INF = 0x3f3f3f3f;
const ll INFF = 0x3f3f3f3f3f3f3f3f;
int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
bool check(ll n) { // 判断n是否为平方数
ll tmp = floor(sqrt(n) + 0.5);
return tmp * tmp == n;
}
int main() {
IOS;
#ifndef ONLINE_JUDGE
clock_t my_clock = clock();
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
// ----------------------------------------------------------------
CaseT{
ll p, q; cin >> p >> q;
int d = gcd(p, q);
if (d != 1) p /= d, q /= d;
ll x = p + 2 * q, y = p - 2 * q;
if (!check(x) || !check(y)) { // 无解
cout << "0 0" << endl;
continue;
}
x = sqrt(x), y = sqrt(y);
ll a = x + y >> 1, b = x - y >> 1;
if (a + b == x && a - b == y) cout << a << ' ' << b << endl; // a和b是整数
else cout << "0 0" << endl;
}
// ----------------------------------------------------------------
#ifndef ONLINE_JUDGE
cout << endl << "Time used " << clock() - my_clock << " ms." << endl;
#endif
return 0;
}
G. Edge Groups
题意
给定一个有 n ( 3 ≤ n ≤ 1 e 5 , n 为 奇 数 ) n\ \ (3\leq n\leq 1\mathrm{e}5,n为奇数) n (3≤n≤1e5,n为奇数)个节点、 ( n − 1 ) (n-1) (n−1)条边的无向连通图,求将边分为 n − 1 2 \dfrac{n-1}{2} 2n−1组且满足如下两条件的方案数,答案对 998244353 998244353 998244353取模:①每组有且仅有两条边;②两条在同一组中的边有一个公共节点.
图用 ( n − 1 ) (n-1) (n−1)行输入描述,每行包含两个正整数 u , v ( 1 ≤ u < v ≤ n ) u,v\ \ (1\leq u<v\leq n) u,v (1≤u<v≤n),表示节点 u u u和 v v v间连有无向边.
解
注意到连通 n n n个节点至少需要 ( n − 1 ) (n-1) (n−1)条边,则本题中的无向连通图是树.
考察以 x x x为根节点的子树的方案数,其中 f a fa fa为 x x x的父节点.如下图,按子树的节点数为奇数、偶数分为两种情况,分别称为I型、II型子树.
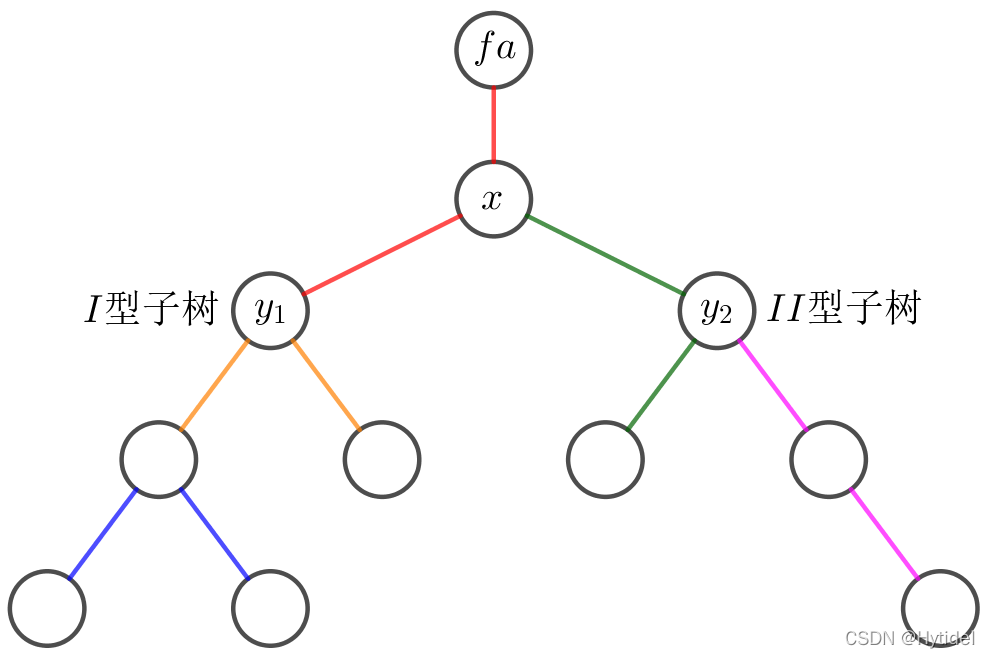
II型子树有偶数个节点,奇数条边,再加上边 ( x , y 2 ) (x,y_2) (x,y2)即可两两配对;I型子树有奇数个节点,偶数条边, y 1 y_1 y1的子树中的边两两配对后,边 ( x , y 1 ) (x,y_1) (x,y1)未配对,可能需与边 ( f a , x ) (fa,x) (fa,x)配对,是否需要用到边 ( f a , x ) (fa,x) (fa,x)取决于 x x x的子树中I型子树的数量的奇偶:①有偶数个时,所有I型子树的边 ( x , y i ) (x,y_i) (x,yi)可两两配对;②有奇数个时,所有I型子树的边 ( x , y i ) (x,y_i) (x,yi)两两配对剩下的一条边与 ( f a , x ) (fa,x) (fa,x)配对.
考察 n ( n 为 偶 数 ) n\ \ (n为偶数) n (n为偶数)条边平均分为 n 2 \dfrac{n}{2} 2n组的方案数 d f a c [ n ] dfac[n] dfac[n]. n = 2 n=2 n=2时, d f a c [ 2 ] = 1 dfac[2]=1 dfac[2]=1; n = 4 n=4 n=4时, d f a c [ 4 ] = C 4 2 C 2 2 A 2 2 = 3 dfac[4]=\dfrac{C_4^2C_2^2}{A_2^2}=3 dfac[4]=A22C42C22=3; n = 6 n=6 n=6时, d f a c [ 6 ] = C 6 2 C 4 2 C 2 2 A 3 3 = 15 dfac[6]=\dfrac{C_6^2C_4^2C_2^2}{A_3^3}=15 dfac[6]=A33C62C42C22=15; n = 8 n=8 n=8时, d f a c [ 8 ] = C 8 2 C 6 2 C 4 2 C 2 2 A 4 4 = 105 dfac[8]=\dfrac{C_8^2C_6^2C_4^2C_2^2}{A_4^4}=105 dfac[8]=A44C82C62C42C22=105.
注意到 d f a c [ 4 ] = d f a c [ 2 ] ∗ 3 , d f a c [ 6 ] = d f a c [ 4 ] ∗ 5 , d f a c [ 8 ] = d f a c [ 6 ] ∗ 7 dfac[4]=dfac[2]*3,dfac[6]=dfac[4]*5,dfac[8]=dfac[6]*7 dfac[4]=dfac[2]∗3,dfac[6]=dfac[4]∗5,dfac[8]=dfac[6]∗7,猜想 d f a c [ n ] = d f a c [ n − 2 ] ∗ ( n − 1 ) dfac[n]=dfac[n-2]*(n-1) dfac[n]=dfac[n−2]∗(n−1),下面证明该结论. d f a c [ n ] = C n 2 C n − 2 2 C n − 4 2 ⋯ C 2 2 A n 2 n 2 , d f a c [ n − 2 ] = C n − 2 2 C n − 4 2 ⋯ C 2 2 A n − 2 2 n − 2 2 dfac[n]=\dfrac{C_n^2C_{n-2}^2C_{n-4}^2\cdots C_2^2}{A_\frac{n}{2}^\frac{n}{2}},dfac[n-2]=\dfrac{C_{n-2}^2C_{n-4}^2\cdots C_2^2}{A_\frac{n-2}{2}^\frac{n-2}{2}} dfac[n]=A2n2nCn2Cn−22Cn−42⋯C22,dfac[n−2]=A2n−22n−2Cn−22Cn−42⋯C22,则 d f a c [ n ] d f a c [ n − 2 ] = C n 2 n 2 = n ! 2 ! ⋅ ( n − 2 ) ! ⋅ 2 n = n − 1 \dfrac{dfac[n]}{dfac[n-2]}=\dfrac{C_n^2}{\dfrac{n}{2}}=\dfrac{n!}{2!\cdot(n-2)!}\cdot\dfrac{2}{n}=n-1 dfac[n−2]dfac[n]=2nCn2=2!⋅(n−2)!n!⋅n2=n−1.
d p [ x ] dp[x] dp[x]表示以节点 x x x为根节点的子树分组的方案数,设其子树的根节点分别为 y i y_i yi,其中有 c n t cnt cnt个I型子树,则状态转移方程 d p [ x ] = { d f a c [ c n t ] ∗ ∏ i d p [ y i ] , c n t 为 偶 数 d f a c [ c n t + 1 ] ∗ ∏ i d p [ y i ] , c n t 为 奇 数 dp[x]=\begin{cases}\displaystyle dfac[cnt]*\prod_i dp[y_i],cnt为偶数 \\ \displaystyle dfac[cnt+1]*\prod_i dp[y_i],cnt为奇数\end{cases} dp[x]=⎩⎪⎨⎪⎧dfac[cnt]∗i∏dp[yi],cnt为偶数dfac[cnt+1]∗i∏dp[yi],cnt为奇数.
代码 -> 2021ICPC上海-G(树形DP+组合计数)
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<unordered_set>
#include<unordered_map>
#include<sstream>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
typedef queue<int> qi;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, double> pdd;
#define umap unordered_map
#define IOS ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
#define CaseT int CaseT; cin >> CaseT; while(CaseT--)
#define endl '\n'
#define so sizeof
#define pb push_back
#define npt nullptr
const double eps = 1e-7;
const int INF = 0x3f3f3f3f;
const ll INFF = 0x3f3f3f3f3f3f3f3f;
const int MAXN = 1e5 + 5, MOD = 998244353;
int n; // 节点数
vi graph[MAXN]; // g[i]=j表示节点i和j间有有向边
int siz[MAXN]; // siz[i]表示以节点i为根节点的子树的大小(节点数)
int dfac[MAXN]; // dfac[n]=1*3*5*...*(n-1),n为偶数
int dp[MAXN]; // dp[i]表示以节点i为根节点的子树分组的方案数
void init() { // 预处理出dfac[]
dfac[0] = 1;
for (int i = 2; i <= n; i += 2) dfac[i] = (ll)dfac[i - 2] * (i - 1) % MOD;
}
void dfs(int u, int fa) { // 当前节点、前驱
siz[u] = 1; // 当前子树的大小初始值为1,即子树的根节点
dp[u] = 1; // 方案数初始化为1
int cnt = 0; // 统计以u为根节点的子树中,节点数为奇数的子树的数量
for (auto& v : graph[u]) { // 注意取引用,因要更新子树的信息
if (v == fa) continue; // 搜过了
dfs(v, u); // 搜以v为根节点的子树,v的前驱为u
// 用子树更新根节点u的信息
siz[u] += siz[v];
dp[u] = (ll)dp[u] * dp[v] % MOD;
if (siz[v] & 1) cnt++; // 更新节点数为奇数的子树的数量
}
if (cnt & 1) cnt++; // 有奇数个节点数为奇数的子树,则需把边(u,fa)一起考虑
dp[u] = (ll)dp[u] * dfac[cnt] % MOD;
}
int main() {
IOS;
#ifndef ONLINE_JUDGE
clock_t my_clock = clock();
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
// ----------------------------------------------------------------
cin >> n;
for (int i = 1; i < n; i++) {
int u, v; cin >> u >> v;
graph[u].push_back(v), graph[v].push_back(u);
}
init(); // 预处理出dfac[]
dfs(1, 0); // 1号节点作为根节点,无前驱,记为0
cout << dp[1];
// ----------------------------------------------------------------
#ifndef ONLINE_JUDGE
cout << endl << "Time used " << clock() - my_clock << " ms." << endl;
#endif
return 0;
}
K. Circle of Life
题意
从左到右,有 n ( 2 ≤ n ≤ 123 ) n\ \ (2\leq n\leq 123) n (2≤n≤123)个节点由 ( n − 1 ) (n-1) (n−1)条边相连,节点编号分别为 1 ∼ n 1\sim n 1∼n.初始状态由一个长度为 n n n的 0 − 1 0-1 0−1串 s s s给出,其中 s [ i ] = 1 s[i]=1 s[i]=1表示节点 i i i处有精灵, s [ i ] = 0 s[i]=0 s[i]=0表示节点 i i i处无精灵( s s s下标从 1 1 1开始),每个节点处最多只有一个精灵.现进行 2 n 2n 2n次变换,每次变换时所有精灵会同时分裂成两个精灵,其中一个精灵向左移动,另一个精灵向右移动.当两个精灵在节点处或边上相遇时会湮灭,在节点 1 1 1处向左移动、在节点 n n n处向右移动的精灵会湮灭.
给定 n n n,求一初始状态$s\ s.t.\ $进行 2 n 2n 2n次变换后至少剩下一个精灵.
解
手动模拟样例可知要在 2 n 2n 2n次变换内出现循环.
样例给出了 n = 2 n=2 n=2和 n = 4 n=4 n=4时的构造,容易猜想 n n n为偶数时都构造 100 ⋯ 0 100\cdots 0 100⋯0,但事实上 n = 6 n=6 n=6时需 14 > 12 14>12 14>12步才能循环.
样例都是偶数,容易想到尝试 n n n为奇数的情况. n = 3 n=3 n=3时易得不存在满足的 s s s; n = 5 n=5 n=5时,先尝试偶数的猜想 10000 10000 10000能否循环. 10000 → 01000 → 10100 → 00010 → 00101 → 01000 10000\rightarrow 01000\rightarrow 10100\rightarrow 00010\rightarrow 00101\rightarrow 01000 10000→01000→10100→00010→00101→01000,出现了 01000 01000 01000的循环.但是这样的循环不能推广,即它连接上其他的循环后的串未必循环,即使循环也未必在 2 n 2n 2n次内循环.
考虑如何用一些自身循环的子串连接成长度为 n n n的串 s s . t . s s\ s.t.\ s s s.t. s在 2 n 2n 2n次内循环.考察可以作为自身循环单元的子串的性质.为使得用它们连接成的串仍能在 2 n 2n 2n次内循环,对任一子串,其在两侧的"行为"应该镜像地相似,则它应是"比较对称"的.
考察哪些”比较对称“的串可作为自身循环单元.尝试得 1001 1001 1001可作为自身循环单元.考虑打表 n = 1 ∼ 7 n=1\sim 7 n=1∼7的自身循环单元 a n s [ ] ans[] ans[],将 n ≥ 8 n\geq 8 n≥8情况按模 4 4 4的余数 r r r分类:① r = 0 r=0 r=0时,输出若干个 1001 1001 1001即可;② r = 1 r=1 r=1时,先输出 a n s [ 5 ] ans[5] ans[5],再 n − = 5 n-=5 n−=5化为①的情况;③ r = 2 r=2 r=2时,先输出 a n s [ 6 ] ans[6] ans[6],再 n − = 6 n-=6 n−=6化为①的情况;④ r = 3 r=3 r=3时,先输出 a n s [ 7 ] ans[7] ans[7],再 n − = 7 n-=7 n−=7化为①的情况.
代码 -> 2021ICPC上海-K(构造)
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<unordered_set>
#include<unordered_map>
#include<sstream>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
typedef queue<int> qi;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, double> pdd;
#define umap unordered_map
#define IOS ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
#define CaseT int CaseT; cin >> CaseT; while(CaseT--)
#define endl '\n'
#define so sizeof
#define pb push_back
#define npt nullptr
const double eps = 1e-7;
const int INF = 0x3f3f3f3f;
const ll INFF = 0x3f3f3f3f3f3f3f3f;
string ans[] = { "X","0","01","X","1001","10001","011001","0101001" };
void solve(int n) {
if (n <= 7) {
cout << ans[n];
return;
}
if (n % 4 == 0) {
for (int i = 0; i < n / 4; i++) cout << ans[4];
return;
}
else if (n % 4 == 1) {
cout << ans[5];
solve(n - 5);
}
else if (n % 4 == 2) {
cout << ans[6];
solve(n - 6);
}
else {
cout << ans[7];
solve(n - 7);
}
}
int main() {
IOS;
#ifndef ONLINE_JUDGE
clock_t my_clock = clock();
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
// ----------------------------------------------------------------
int n; cin >> n;
if (n == 3) return cout << "Unlucky", 0; // 特判无解
solve(n);
// ----------------------------------------------------------------
#ifndef ONLINE_JUDGE
cout << endl << "Time used " << clock() - my_clock << " ms." << endl;
#endif
return 0;
}
I. Steadily Growing Steam ( 512 M B 512\ \mathrm{MB} 512 MB)
题意
有 n ( 1 ≤ n ≤ 100 ) n\ \ (1\leq n\leq 100) n (1≤n≤100)张牌,每张牌有一个价值 v i ( ∣ v i ∣ ≤ 1 e 9 ) v_i\ \ (|v_i|\leq 1\mathrm{e}9) vi (∣vi∣≤1e9)和点数 t i ( 1 ≤ t i ≤ 13 ) t_i\ \ (1\leq t_i\leq 13) ti (1≤ti≤13).先选择至多 k ( 0 ≤ k ≤ n ) k\ \ (0\leq k\leq n) k (0≤k≤n)张牌将其点数翻倍,再从 n n n张牌中选若干张牌分成两堆,要求两堆内点数之和相等,求选出的牌的价值之和的最大值.
解I
将牌视为物品,点数视为体积,转化为背包.
设两堆的点数之和分别为 A A A和 B B B.注意到不关心 A A A和 B B B的具体数值,只关心它们是否相等,则可用 A − B A-B A−B作为 0 − 1 0-1 0−1背包的体积,即视放入 A A A堆的体积为正,放入 B B B堆的体积为负.初始点数 t t t最大 13 13 13,翻倍后最大 26 26 26,最多 100 100 100张牌,则体积范围 ( − 2600 , 2600 ) (-2600,2600) (−2600,2600).因数组的下标非负,可加一个 2600 2600 2600的偏移量.
d p [ i ] [ j ] [ w ] dp[i][j][w] dp[i][j][w]表示只考虑前 i i i张牌、还可以翻倍 j j j次、当前背包体积为 w w w的价值之和的最大值, d p [ 100 ] [ 100 ] [ 5200 ] dp[100][100][5200] dp[100][100][5200],最终答案 a n s = max 0 ≤ j ≤ k d p [ n ] [ j ] [ 2600 ] ans=\displaystyle \max_{0\leq j\leq k} dp[n][j][2600] ans=0≤j≤kmaxdp[n][j][2600].
考虑最后一个不同点,即已考虑完前 ( i − 1 ) (i-1) (i−1)张牌,现考虑第 i i i张牌.
状态转移方程 d p [ i ] [ j ] [ w ] = max { d p [ i − 1 ] [ j ] [ w ] , 不 选 t i d p [ i − 1 ] [ j ] [ w + t i ] + v i , t i 放 入 A d p [ i − 1 ] [ j ] [ w − t i ] + v i , t i 放 入 B d p [ i − 1 ] [ j − 1 ] [ w + 2 ∗ t i ] + v i , 2 t i 放 入 A d p [ i − 1 ] [ j − 1 ] [ w − 2 ∗ t i ] + v i , 2 t i 放 入 B dp[i][j][w]=\max\begin{cases}dp[i-1][j][w],不选t_i \\ dp[i-1][j][w+t_i]+v_i,t_i放入A \\ dp[i-1][j][w-t_i]+v_i,t_i放入B \\ dp[i-1][j-1][w+2*t_i]+v_i,2t_i放入A \\ dp[i-1][j-1][w-2*t_i]+v_i,2t_i放入B\end{cases} dp[i][j][w]=max⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧dp[i−1][j][w],不选tidp[i−1][j][w+ti]+vi,ti放入Adp[i−1][j][w−ti]+vi,ti放入Bdp[i−1][j−1][w+2∗ti]+vi,2ti放入Adp[i−1][j−1][w−2∗ti]+vi,2ti放入B,第一维 O ( n ) O(n) O(n),第二维 O ( k ) O(k) O(k),第三维 O ( 4 n t ) O(4nt) O(4nt),转移 O ( 1 ) O(1) O(1),总时间复杂度 O ( n ⋅ k ⋅ 4 n t ) ≈ O ( 4 n 3 t ) O(n\cdot k\cdot 4nt)\approx O(4n^3t) O(n⋅k⋅4nt)≈O(4n3t),看起来 1 s 1\ \mathrm{s} 1 s不够,但事实上很多方案不合法,故实际方案数远小于 O ( 4 n 3 t ) O(4n^3t) O(4n3t).
物品价值数量级 1 e 9 1\mathrm{e}9 1e9,最多 100 100 100个物品,故dp数组要开ll.空间复杂度 100 × 100 × 5200 × 8 ÷ 1024 ÷ 1024 ≈ 397 M B < 512 M B 100\times 100\times 5200\times 8\div 1024\div 1024\approx 397\ \mathrm{MB}<512\ \mathrm{MB} 100×100×5200×8÷1024÷1024≈397 MB<512 MB,空间足够.
代码I -> 2021ICPC上海-I(背包DP)
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<unordered_set>
#include<unordered_map>
#include<sstream>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
typedef queue<int> qi;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, double> pdd;
#define umap unordered_map
#define IOS ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
#define CaseT int CaseT; cin >> CaseT; while(CaseT--)
#define endl '\n'
#define so sizeof
#define pb push_back
#define npt nullptr
const double eps = 1e-7;
const double pi = acos(-1);
const int INF = 0x3f3f3f3f;
const ll INFF = 0x3f3f3f3f3f3f3f3f;
const int MAXN = 105, MAXM = 5205;
int n, k; // 牌数、最多翻倍次数
int v[MAXN], t[MAXN]; // 价值、点数
// dp[i][j][w]表示只考虑前i个物品、还可翻倍j次、当前背包体积为w的价值之和最大值
ll dp[MAXN][MAXN][MAXM];
int main() {
IOS;
#ifndef ONLINE_JUDGE
clock_t my_clock = clock();
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
// ----------------------------------------------------------------
memset(dp, -INFF, so(dp)); // 置为-INFF,表示未更新
dp[0][0][2600] = 0; // k=2600为答案
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> v[i] >> t[i];
for (int i = 1; i <= n; i++) { // 枚举物品
for (int j = 0; j <= k; j++) { // 枚举翻倍次数
for (int w = 0; w <= 5200; w++) { // 枚举背包体积
if (dp[i - 1][j][w] != -INFF) dp[i][j][w] = dp[i - 1][j][w]; // 不选t[i]
if (w >= t[i] && dp[i - 1][j][w - t[i]] != -INFF) // t[i]放入A
dp[i][j][w] = max(dp[i][j][w], dp[i - 1][j][w - t[i]] + v[i]);
if (w <= 5200 - t[i] && dp[i - 1][j][w + t[i]] != -INFF) // t[i]放入B
dp[i][j][w] = max(dp[i][j][w], dp[i - 1][j][w + t[i]] + v[i]);
if (j && w >= 2 * t[i] && dp[i - 1][j - 1][w - 2 * t[i]] != -INFF) // 2*t[i]放入A
dp[i][j][w] = max(dp[i][j][w], dp[i - 1][j - 1][w - 2 * t[i]] + v[i]);
if (j && w <= 5200 - 2 * t[i] && dp[i - 1][j - 1][w + 2 * t[i]] != -INFF) // 2*t[i]放入B
dp[i][j][w] = max(dp[i][j][w], dp[i - 1][j - 1][w + 2 * t[i]] + v[i]);
}
}
}
ll ans = -INFF;
for (int j = 0; j <= k; j++) ans = max(ans, dp[n][j][2600]);
cout << ans;
// ----------------------------------------------------------------
#ifndef ONLINE_JUDGE
cout << endl << "Time used " << clock() - my_clock << " ms." << endl;
#endif
return 0;
}
解II:滚动数组优化 (By 暮冥)
dp数组的第一维滚动.
代码II -> 2021ICPC上海-I(背包dp+滚动数组优化)
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<iomanip>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<unordered_set>
#include<unordered_map>
#include<sstream>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
typedef queue<int> qi;
typedef pair<int, int> pii;
typedef pair<ll, ll> pll;
typedef pair<double, double> pdd;
#define umap unordered_map
#define IOS ios::sync_with_stdio(0); cin.tie(0), cout.tie(0);
#define CaseT int CaseT; cin >> CaseT; while(CaseT--)
#define endl '\n'
#define so sizeof
#define pb push_back
#define npt nullptr
const double eps = 1e-7;
const double pi = acos(-1);
const int INF = 0x3f3f3f3f;
const ll INFF = 0x3f3f3f3f3f3f3f3f;
const int MAXN = 105, MAXM = 2605;
int n, k; // 牌数、最多翻倍次数
int v[MAXN], t[MAXN]; // 价值、点数
// dp[i][j][w]表示只考虑前i个物品、还可翻倍j次、当前背包体积为w的价值之和最大值
ll dp[2][MAXN][MAXM]; // 第一维滚动
int T = 1300; // 偏移量
int idx; // 滚动数组下标
int main() {
IOS;
#ifndef ONLINE_JUDGE
clock_t my_clock = clock();
freopen("in.txt", "r", stdin);
freopen("out.txt", "w", stdout);
#endif
// ----------------------------------------------------------------
memset(dp, -INFF, so(dp)); // 置为-INFF,表示未更新
dp[0][0][T] = 0; // 初始条件,都不选
idx = 1; // 滚动数组下标从1开始
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> v[i] >> t[i];
for (int i = 1; i <= n; i++) { // 枚举物品
memset(dp[idx], -INFF, so(dp[idx])); // 初始化将要更新的部分
for (int j = 0; j <= k; j++) { // 枚举翻倍次数
for (int w = -1300; w <= 1300; w++) { // 枚举背包体积
for (int p = -2; p <= 2; p++) { // 枚举选择的物品,分别为-2*t[i],-t[i],0,t[i],2*t[i]
int curw = w + p * t[i]; // 当前背包体积
if (curw < -1300 || curw>1300) continue; // 越界
if (j) { // 可以翻倍
dp[idx][j][curw + T] = max(dp[idx][j][curw + T], dp[idx ^ 1][j - (abs(p) == 2)][w + T] + (p == 0 ? 0 : v[i]));
}
else if (abs(p) <= 1) // 只能转移不翻倍的
dp[idx][j][curw + T] = max(dp[idx][j][curw + T], dp[idx ^ 1][j][w + T] + (p == 0 ? 0 : v[i]));
}
}
}
idx ^= 1;
}
ll ans = -INFF;
for (int i = 0; i <= k; i++) ans = max(ans, dp[n & 1][i][T]);
cout << ans;
// ----------------------------------------------------------------
#ifndef ONLINE_JUDGE
cout << endl << "Time used " << clock() - my_clock << " ms." << endl;
#endif
return 0;
}
优化空间的效果:如下图,下为朴素,上为滚动数组优化.
