动态规划的误区避免、套路总结与常见题解析
常见大坑：
关于动态规划，老师不会告诉你现在学习的状态转换方程以后用不到，校内动态规划的学习非常基础，它只举出常见的几个例题，类似于要求你背例题。想着让你触类旁通，我明明白白告诉你，可能性几乎为0。
因为每道题都有属于自己的解，而题目在不停的更新，你学的动态转换方程会随题目而改变，因此真正笔试做题没用，只是告诉面试官，我是科班出来的。我学过动态转换，至于能不能解出题目，那是另外一回事。
下面是动态转换的要点，我可以向你保证，你在网上找动态规划入门的教程，找不到比我写的更好的
你在网上找的许多题解，有关动态规划的，几乎是看不懂的，你会惊讶于他们怎么想到的，感觉差距这么大，惊为天人。
网上总有那么一些人，他们通过数学规律得出解，优化后，通过解出的答案去死扣理由，然后把扣出来的理由发到网上，你找的绝大部分题解正是他们扣出来的二次加工后的产物，为的就是显得他们很聪明，为的就是让你佩服他，听明白没有，都是这种货色。
动态规划核心 ：
动态规划的解题核心内容就是对表的解进行优化(俗称打表找规律)，
动态规划的难点在于试法，教课书上的那些状态转移方程是别人在打表之后，在表中找出数学规律之后，才写出来的。也就是说，要已知解，才能写出状态转移方程。(搞笑，我已经知道答案还写个毛方程)
动态规划试法的优化（例如斜率优化）核心是通过邻接位置，代替枚举行为。
动态规划的套路：
尝试——记忆化搜索——优化(打表找规律)——严格表结构dp——精致dp
尝试原则：
原则1：单可变参数最好只是一个值（单可变参数维度最好为低维（0维度））
原则2：可变参数个数少（越少越好找规律）
由于找数学规律不需要理由， 因此不建议在优化的时候找理由（纯装B）
题目1：整数拆分问题
- 使用动态规划法求解整数拆分问题。动态规划函数（状态转移方程），真代码/伪代码，动态规划数组dp。
解法：
设f(n,k)为n的k拆分的拆分方法数
N表示要拆分的数字，k表示最多能被拆成k个的所有情况
n=4，k=4：
4—1+1+1+1
2+1+1
3+1
4
-------------------------------------------------------
n=4，k=3：
4—2+1+1
3+1
4
---------------------------------------------------------
n=4，k=2：
4—3+1
4
------------------------------------
n=4，k=1：
4—4
1.算出一些解
2.打表（根据你算出来的解，填表）如下
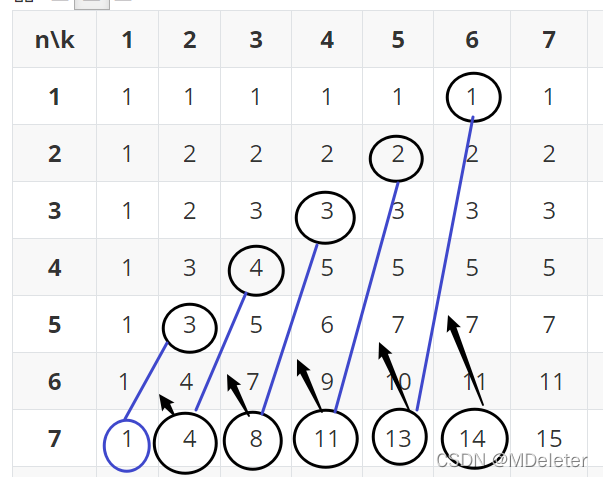
如上图所示，打表后对解进行优化。
可得出规律：f(n,k)=f(n-k,k)+f(n,k-1)
因此，在找出规律后
可以总结出
动态规划步骤就这么简单，算出前面几个解后，填表，找规律，就能求出解，
真正的难点在于试法（这个表该怎么画，是应该一维的还是二维的，变量要怎么选，要选几个），清楚了如何去试之后，解题就没什么难点，后面重点就是优化了。
题目2:0/1背包问题
- 使用动态规划法求解0/1背包问题。动态规划函数（状态转移方程），真代码/伪代码，动态规划数组dp。
解法：
使用上述打表法解此题：
dp[i][r]:
i代表可选物品{1,2,3,4…i}
r代表背包的剩余容积
整个dp[i][r]代表在可选物品中选出不超重物品的最大价值。
此问题中w1-w5{2,2,6,5,4}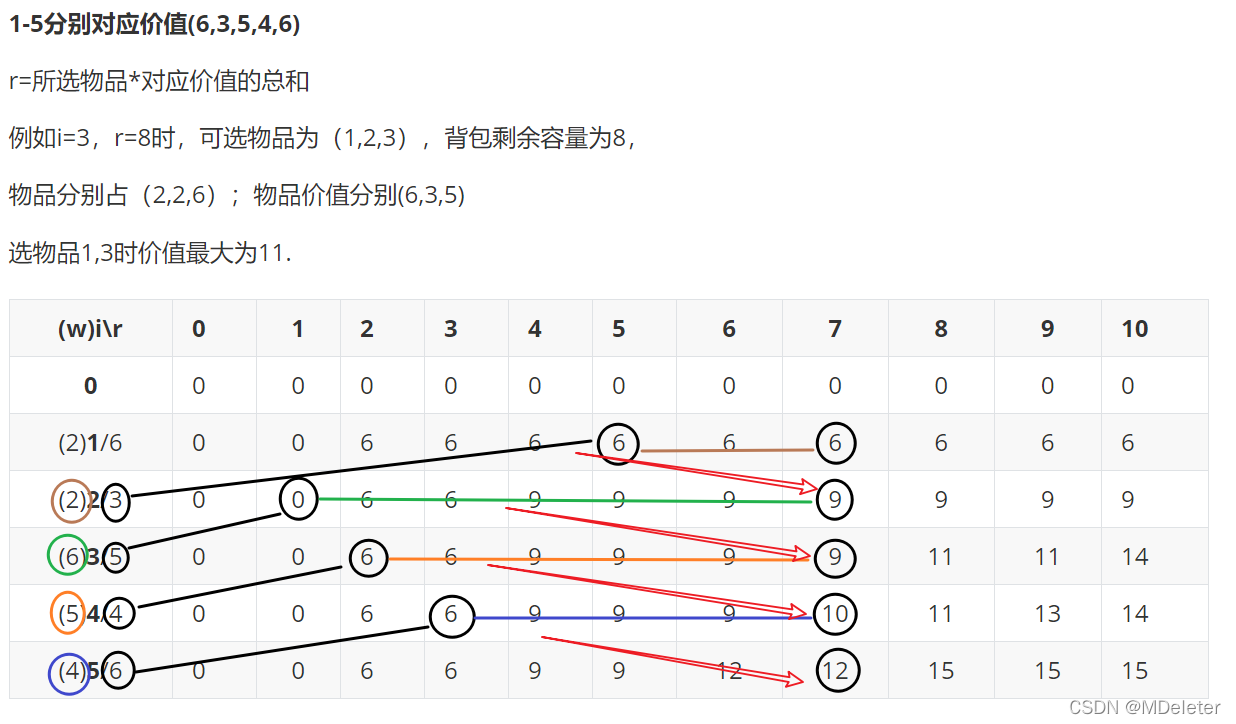
通过打表可以找到上述规律，可通过此规律完成动态转换方程：
dp[i][r] = max(dp[i-1][r],dp[i-1][r-w[i]]+v[i])
如果硬要掰理由，那么方程含义应为：
此行此列最大价值为上一行此列最大价值与(上行-wi列最大价值+vi)之间的最大值
翻译一下：
上一行此列最大价值：没有选第i个物品的最大价值
上行-wi列最大价值+vi：没有选第i-1个物品但选了第i个物品的最大价值。
因此，此题解的核心就是对第i个物品（不选/选）所得出的最大价值进行讨论。
不选——0
选——1
因此背包问题又叫0/1背包问题。
上面的各个结果隐式地排除了选择物品i后超重的情况，因为超重在打表的时候就已经被排除了。
题目3：最大连续字序列和
- 使用动态规划法求解最大连续子序列和。动态规划函数（状态转移方程），真代码/伪代码，动态规划数组dp。
解法：
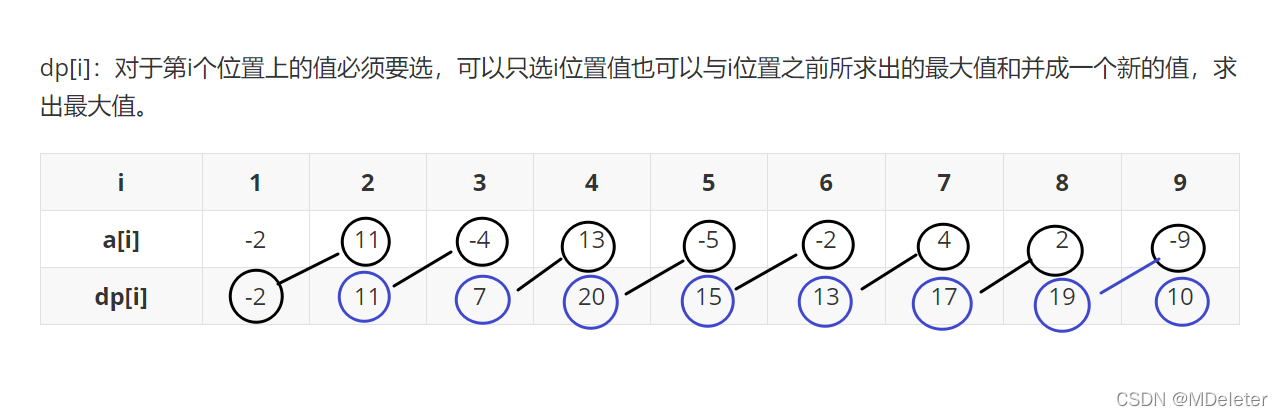
通过打表，可以找到如下规律
dp[i] = max(a[i],a[i]+dp[i-1])
本题并不难以理解，但值得学习的地方并不是动态规划，而在于空间压缩，
按照所打表，dp[i]的空间复杂度为O(n)：将每一个i对应的dp[i]都保存下来。
就本题而言完全没必要用到如此大的空间，事实上可以做到空间复杂度为O(2)
一个用来存储当前更新的dp[i]，一个用来保存max。
Java源代码：
题目4：最长公共子序列
- 使用动态规划法求解最长公共子序列问题。动态规划函数（状态转移方程），真代码/伪代码，动态规划数组dp。 第四章 最长公共子序列 **
解法：
本题为经典动态规划问题，不要将子串和子序列弄混。
Str1长度为M，str2长度为N，生成MxX的动态规划表，从上到下，从左到右计算dp。
dp[i][j]:str1[0..i]与str2[0..j]的最长公共子序列的长度
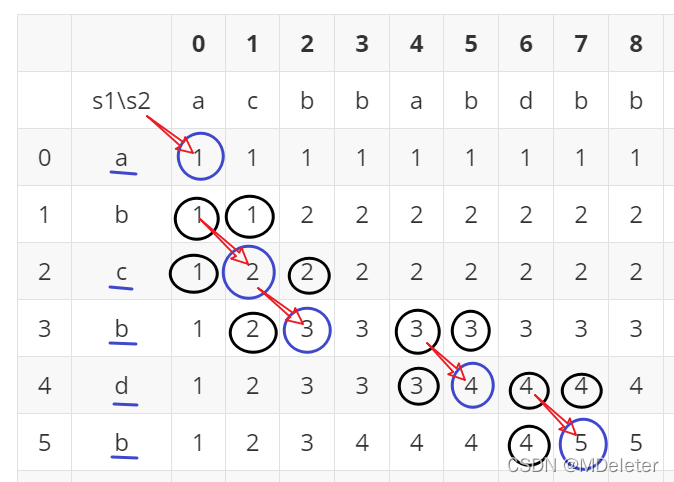
通过打表后可得如下规律：
dp[i][j]依赖于三个位置，左上，左，上。
且当更新最长公共子序列时：
dp[i][j]=dp[i-1][j-1]+1
其他情况
dp[i][j]=Max(dp[i-1][j],dp[i][j-1])
求子序列时可从表的右下方，只按两个方向（左，上）朝左上方向移动。(注意先向上移动，再向左移动)
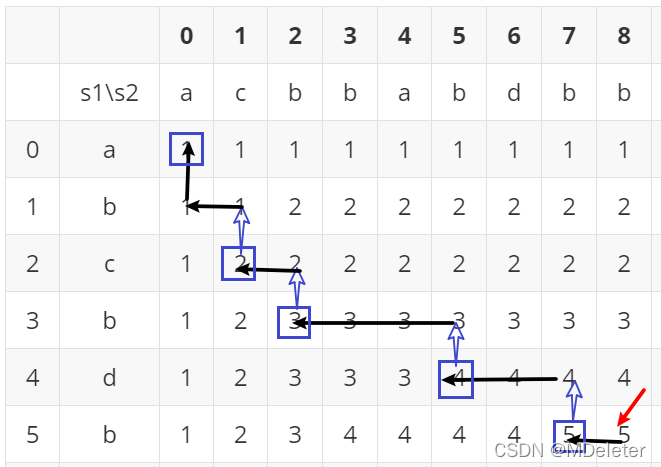
如果dp[i][j]大于dp[i-1][]和dp[i][j-1] ,说明之前在计算dp[i][j]的时候,一定是选
则了，决策dp[i-1][j-1]+1,可以确定str1[i]等于str2[j]，并且这个字符属于最长公共子序列，将这个字符放入res，然后继续先向上移动，再向左移动。
题目5：机器人移动
- 一个机器人只能向下和向右移动，每次只能移动一步。设计一个算法求它从(0,0)
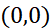移到到(m,n)
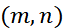有多少条路径。动态规划函数（状态转移方程），真代码/伪代码，动态规划数组dp。
（本题为LeetCode动态规划专题原题——不同路径I）
解法
打表如下：
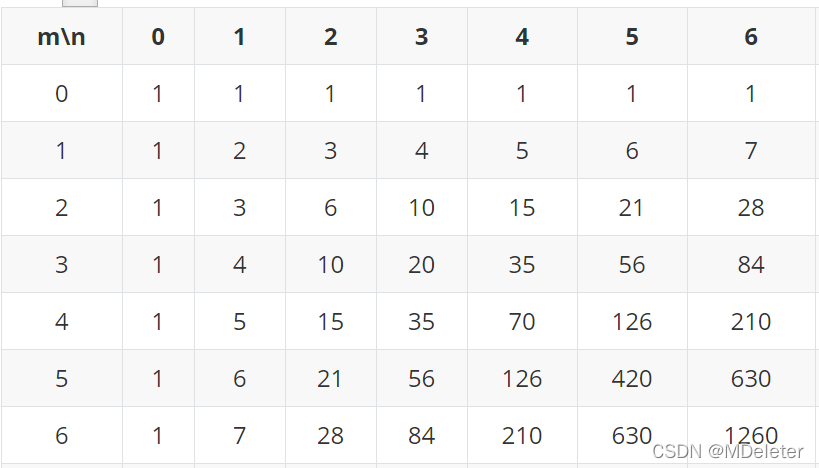
通过找数学规律，写出状态转换方程：
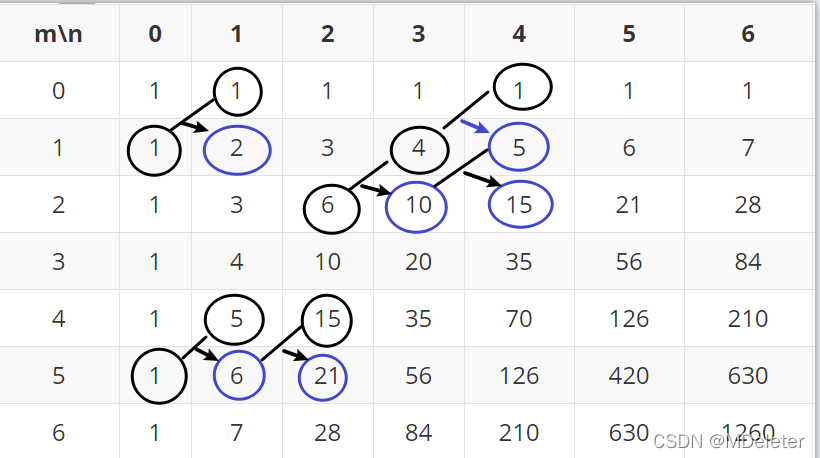
有以下规律：
dp[i][j]=dp[i-1][j]+dp[i][j-1]
本题同样可以使用空间压缩技巧：
观察发现其实
第0行只需要 第1行第0个元素 就能更新为第1行
第1行只需要 第2行第0个元素 就能更新为第2行
第2行只需要 第3行第0个元素 就能更新为第3行
。。。。。
因此已知第0行和第0列可以将整张表压缩为一行。空间复杂度O（n）
而已知第0行和第0列的元素值为1，因此甚至可以将整表压缩到一个位置上
空间复杂度O(1)(可想而知时间复杂度得多高)
动态规划理解起来的确困难，因为要给数学规律一个合理的解释是非常耗费时间的，即使已知在数学规律的背后一定会有原因，但将题做出来跟理解题目不是一个概念，无论你准备朝哪个方向努力。首要的事就是先将题拿下。