解递归式方法
分解:将原问题划分成形式相同的子问题,规模可以不等,对半或2/3对1/3的划分。
解决:对于子问题的解决,很明显,采用的是递归求解的方式,如果子问题足够小了,就停止递归,直接求解。
合并:将子问题的解合并成原问题的解。
这里引出了一个如何求解子问题的问题,显然是采用递归调用栈的方式。因此,递归式与分治法是紧密相连的,使用递归式可以很自然地刻画分治法的运行时间。所以,如果你要问我分治与递归的关系,我会这样回答:分治依托于递归,分治是一种思想,而递归是一种手段,递归式可以刻画分治算法的时间复杂度。
解递归式:
这里有三种方法:代入法、递归树法和主方法。
代入法:
定义:先猜测某个界的存在,再用数学归纳法去证明该猜测的正确性。
缺点:只能用于解的形式很容易猜的情形。
总结:这种方法需要经验的积累,可以通过转换为先前见过的类似递归式来求解。
递归树法:
起因:代换法有时很难得到一个正确的好的猜测值。
用途:画出一个递归树是一种得到好猜测的直接方法。
分析(重点):在递归树中,每一个结点都代表递归函数调用集合中一个子问题的代价。将递归树中每一层内的代价相加得到一个每层代价的集合,再将每层的代价相加得到递归式所有层次的总代价。
总结:递归树最适合用来产生好的猜测,然后用代换法加以验证。
递归树的方法非常直观,总的代价就是把所有层次的代价相加起来得到。但是分析这个总代价的规模却不是件很容易的事情,有时需要用到很多数学的知识。
主方法:
主方法是最好用的方法,书本上以”菜谱“来描述这种方法的好用之处,它可以瞬间估计一个递推式的算法复杂度。但是我们知道,这后面肯定是严格的数学证明在支撑着,对于我们用户来说,我们只用知道怎么用就行了。
优点:针对形如T(n) = af(n/b) + f(n)的递归式
缺点:并不能解所有上述形式的递归式,有一些特殊情况,见下文分析。
分析:三种情况,如下图,着重看圈线的部分:

直觉:看 f(n) 和 n^logb ^ a 的关系,谁大取谁,相等则两个相乘,但要注意看是否相差因子 nε。对于3),还要看是否满足条件 af(n/b) <= cf(n) .
就像上面所说的,该方法不能用于所有的形如上式的递归式,f(n)和n^logb ^ a的关系必须是多项式意义上的小于大于,即渐近关系(渐近小于、渐近大于),什么是渐近,就是两者相差一个因子nε。所以,在情况1和情况2之间有一定的间隙,同样情况2和请看3之间也有一定的间隙;对于情况3,还要看是否满足正则条件。
例子:
代入法:(凭直觉、经验)
1)、习题4.3-1:T(n) = T(n-1) + n

2)、习题4.3-2:T(n) = T(n/2) + 1

递归树法:
1)、对递归式T(n) = 3T(n/2) +n,利用递归树确定一个好的渐近上界,用代入法进行验证。

2)、对递归式T(n) = T(n/2) + n2,利用递归树确定一个好的渐近上界,用代入法进行验证。

主方法:
1)、对于下列递归式,使用主方法求出渐近紧确界。
a、T(n) = 2T(n/4) + 1
b、T(n) = 2T(n/4) + n^1/2
c、T(n) = 2T(n/4) + n
d、T(n) = 2T(n/4) + n^2
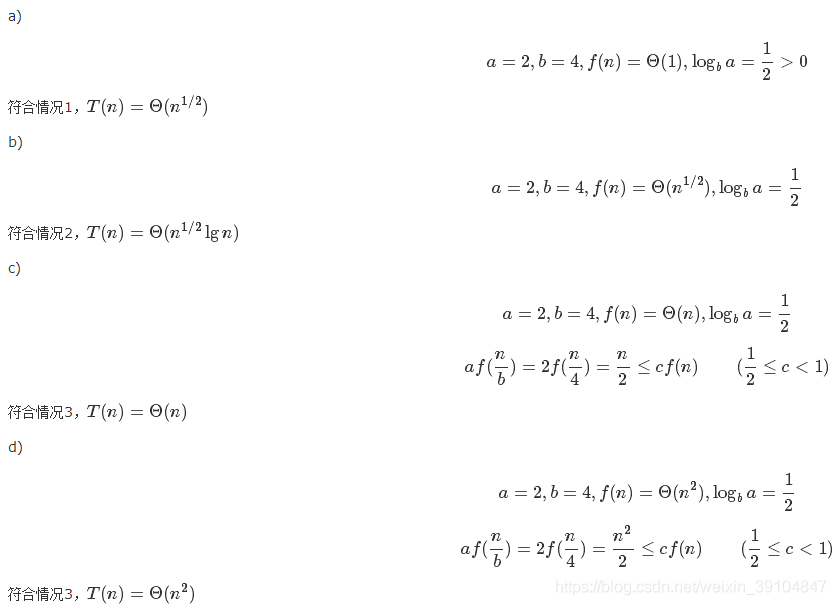
e. T(n) = 3T(n/4) + nlgn
我们有 a = 3,b = 4,f(n) = nlgn,因此n^logb ^ a = nlog4^3 = O(n^0.793) 。由于 f(n) = Θ(nlgn) = Ω(n) = Ω(n^0.793+0.207),因此可以考虑应用于情况3,其中 ε = 0.207。但需要检查是否满足条件:当 n 足够大时,存在 c<1 使 af(n/b) ≤ cf(n) 。
令 3f(n/4) ≤ cf(n) 有
3n/4lg(n/4) ≤ cnlgn
3/4(lgn - lg4) ≤ clgn
(3/4 - c)lgn ≤ 3/4lg4
容易发现,当 c ≥ 3/4 时,上式对于足够大的 n 恒成立。因此可以使用主定理的情况3,得出递归式的解为 T(n) = Θ(nlgn) 。