【记录CF】Codeforces Round #775 (Div. 2) A~C 题解

目录

杂谈

A. Game

B. Game of Ball Passing

C. Weird Sum

---

杂谈

这场A题读题读假了，直接崩掉，一开始以为能一直跳，就去算每两块连续陆地之间的差值了，交了一发WA了，又仔细地读了一遍题，才看到那里加粗了几个词，no more than once jump......

B题推出来答案为 0 和为 1 的情况，然后卡在了计算不为 1 的情况上（讲道理自己给自己搞复杂了，还去计算了每两个人之间的差值），后来发现剩下的情况的答案就是最多的次数减去剩下的次数和。

C题发现性质后又卡在了怎么求每对之间的横、纵距离值，写出来之后答案怎么都不对，最后发现还是式子写错了，极限修改......

总之这场自己出了各种问题，不说了，继续训练......

A. Game

题目链接：Problem - A - Codeforces

题目大意：给定一个序列，1代表陆地，0代表水，如果陆地相邻可以直接走过去，如果中间隔着水，那可以消耗两个陆地之间的距离的硬币数进行跳跃，只能进行一次跳跃，问从最左端到达最右端的最小花费硬币数是多少。

解题思路：注意只能进行一次跳跃，那么只需要判断左边和右边陆地最多连续到第几个位置，进行相减就是最小花费硬币数。

AC代码：

#include <bits/stdc++.h>
#define lowbit(x) (x & -x)
#define mid (l + r >> 1)
 
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 105;
int a[N];
 
int main(){
    //freopen("input.txt", "r", stdin);
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin >> t;
    while(t--){
    	int n;
    	cin >> n;
    	for(int i = 1; i <= n; i++) cin >> a[i];
    	int posl = 0, posr = 0;
    	for(int i = n; i >= 1; i--){
    		if(!a[i]){
    			posr = i + 1;
    			break;
    		}
    	}
    	for(int i = 1; i <= n; i++){
    		if(!a[i]){
    			posl = i - 1;
    			break;
    		}
    	}
    	cout << posr - posl << endl;
    }
    return 0;
}

B. Game of Ball Passing

题目链接：Problem - B - Codeforces

题目大意：给定一个序列，序列中第 i 个数表示 i 号球员进行的传球次数，求在这场传球中，最少可能有多少颗球。

解题思路：如果让传球次数最多的人先传，比如：1，5，2这个例子中，让2号球员先传，过程为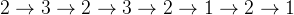，2号球员还剩下一次次数，就需要多一颗球进行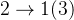这样一个过程。可以发现，如果传球次数最多的人的传球次数比其他人传球次数总和 + 1还多，那么说明他们不可能只使用了一颗球，因为一颗球只能让最多的传球次数减少其他人传球次数的总和+1，这样剩下的次数就是还需要多加的球数。

AC代码：

#include <bits/stdc++.h>
#define lowbit(x) (x & -x)
#define mid (l + r >> 1)

using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1000000007;

int main(){
    //freopen("input.txt", "r", stdin);
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin >> t;
    while(t--){
    	int n;
    	cin >> n;
    	ll sum = 0, maxa = -1;
    	for(int i = 1; i <= n; i++){
    		ll a;
    		cin >> a;
    		sum += a;
    		maxa = max(maxa, a);
    	}
    	if(sum == 0) cout << 0 << endl;
    	else if(maxa * 2 <= sum) cout << 1 << endl;
    	else cout << maxa * 2 - sum << endl;
    }
    return 0;
}

C. Weird Sum

题目链接：Problem - C - Codeforces

题目大意：给定一个矩阵，求每对相同元素之间的曼哈顿距离总和。

解题思路：考虑曼哈顿距离的性质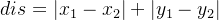，，可以发现横坐标和纵坐标是可以分开进行计算的，对于求所有的总和，可以分别求所有的横、纵坐标计算的和。

以求纵坐标和为例，对于某个点来说，假设前面出现过的相同元素都在该行，那么纵距离的和就是0，启发我们可以这样进行计算：将前面出现的相同元素的数所在行数进行累加，记为 sum，出翔的相同元素的个数记为 num，那么数的个数 num 乘上当前行数 i 再减去累加的值 sum 就是当前这个数和前面所有相同元素的纵距离之和，即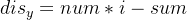。横坐标距离和求法也是相同的，这样最后累加的结果就是答案了。

AC代码：

#include <bits/stdc++.h>
#define lowbit(x) (x & -x)
#define mid (l + r >> 1)

using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 100005;
ll a[N], num1[N], num2[N], sum1[N], sum2[N];

int main(){
    //freopen("input.txt", "r", stdin);
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    ll n, m, x;
    cin >> n >> m;
    ll ansx = 0, ansy = 0;
    for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++){
			cin >> x;
			a[(i - 1) * m + j] = x;
			ansy += num1[x] * i - sum1[x];
			sum1[x] += i;
			num1[x]++;
		}
	}
	for(int i = 1; i <= m; i++){
		for(int j = 1; j <= n; j++){
			x = a[(j - 1) * m + i];
			ansx += num2[x] * i - sum2[x];
			sum2[x] += i;
			num2[x]++;
		}
	}
	cout << ansx + ansy << endl;
    return 0;
}