matlab 取图像一部分微分算子,Matlab实现：图像边缘提取

1、边缘提取算法

方法一：一阶微分算子

Sobel算子

Sobel算子检测方法对灰度渐变和噪声较多的图像处理效果较好，Sobel算子对边缘定位不是很准确，图像的边缘不止一个像素。

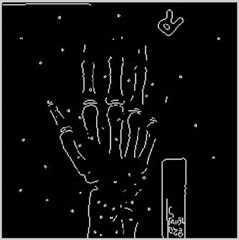
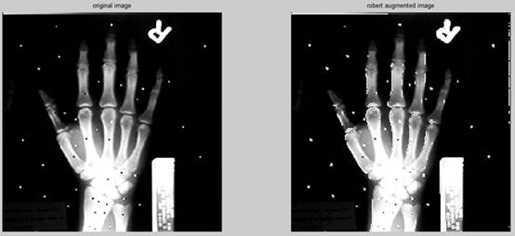
Roberts算子

Roberts算子检测方法对具有陡峭的低噪声的图像处理效果较好，但是利用roberts算子提取边缘的结果是边缘比较粗，因此边缘的定位不是很准确。

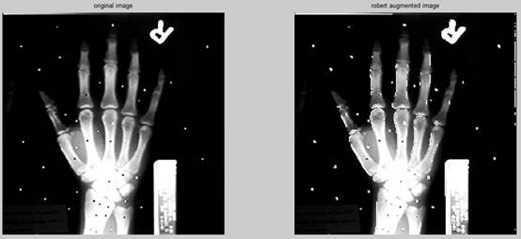
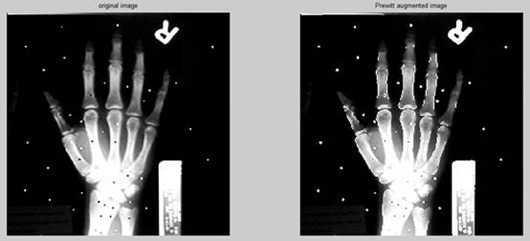
Prewitt算子

Prewitt算子检测方法对灰度渐变和噪声较多的图像处理效果较好。但边缘较宽，而且间断点多。

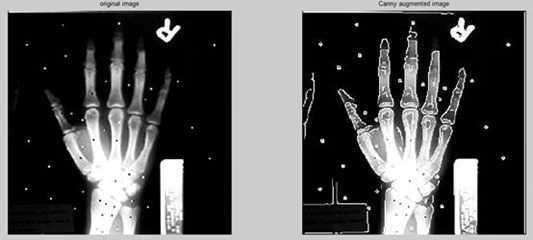
Canny算子

Canny算子是目前边缘检测最常用的算法，效果也是最理想的。

Canny边缘检测算法不是简单的模板卷积而已，通过梯度方向和双阈值法来检测边缘点，具体算法可以参考：http://www.cnblogs.com/AndyJee/p/3734805.html；

Canny方法不容易受噪声干扰，能够检测到真正的弱边缘。优点在于，使用两种不同的阈值分别检测强边缘和弱边缘，并且当弱边缘和强边缘相连时，才将弱边缘包含在输出图像中。

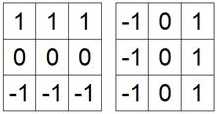
方法二：二阶微分算子

Laplacian算子

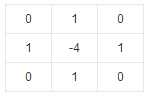
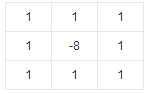
Laplacian算子法对噪声比较敏感，所以很少用该算子检测边缘，而是用来判断边缘像素视为与图像的明区还是暗区。

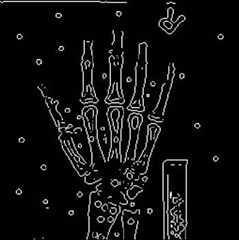
2、实验结果分析

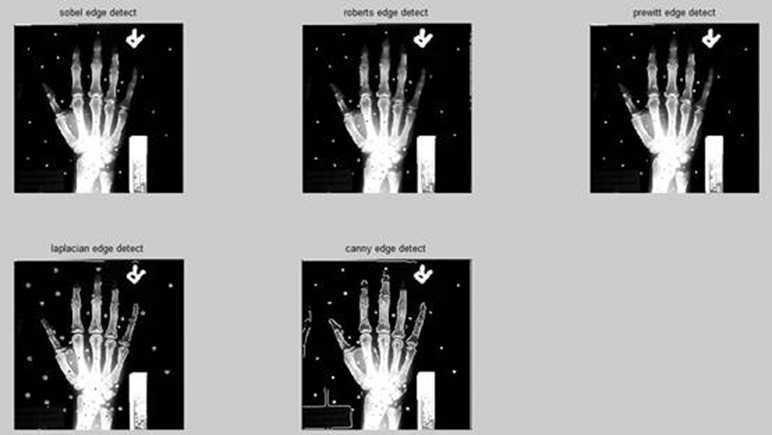
一、边缘提取：

Sobel算子检测方法对灰度渐变和噪声较多的图像处理效果较好，sobel算子对边缘定位不是很准确，图像的边缘不止一个像素；

Roberts算子检测方法对具有陡峭的低噪声的图像处理效果较好，但是利用roberts算子提取边缘的结果是边缘比较粗，因此边缘的定位不是很准确；

Prewitt算子检测方法对灰度渐变和噪声较多的图像处理效果较好。但边缘较宽，而且间断点多；

Laplacian算子法对噪声比较敏感，所以很少用该算子检测边缘，而是用来判断边缘像素视为与图像的明区还是暗区；

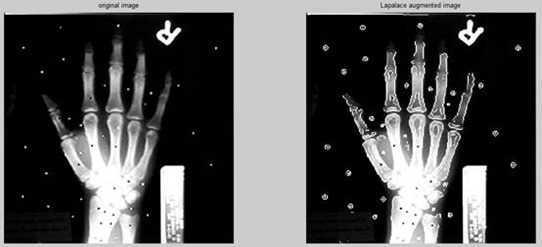
二、边缘复合增强

Sobel、Robert、Prewitt算子的增强效果并不是很明显，尤其是Robert算子，因为它提取的边缘点过于稀疏和离散；

Laplacian算子和canny算子的增强效果都比较理想，

将边缘叠加上去后，整个手的轮廓和边缘都很清晰，直观上看，canny算子实现的效果比Laplacian算子好，最明显的地方就是手指尖的边缘。

3、程序实现

下面的程序就实现上面效果的完整Matlab代码：

clear;clc;

I=imread(‘x1.tif‘);

% I=rgb2gray(I);

% gray transform

J=imadjust(I,[0.1 0.9],[0 1],1);

% Edge detection

% Sobel

BW1=edge(I,‘sobel‘);

sobelBW1=im2uint8(BW1)+J;

figure;

%imshow(BW1);

subplot(1,2,1);

imshow(J);

title(‘original image‘);

subplot(1,2,2);

imshow(sobelBW1);

title(‘Sobel augmented image‘);

% Roberts

BW2=edge(I,‘roberts‘);

robertBW2=im2uint8(BW2)+J;

figure;

%imshow(BW2);

subplot(1,2,1);

imshow(J);

title(‘original image‘);

subplot(1,2,2);

imshow(robertBW2);

title(‘robert augmented image‘);

% prewitt

BW3=edge(I,‘prewitt‘);

prewittBW3=im2uint8(BW3)+J;

figure;

%imshow(BW3);

subplot(1,2,1);

imshow(J);

title(‘original image‘);

subplot(1,2,2);

imshow(prewittBW3);

title(‘Prewitt augmented image‘);

% log

BW4=edge(I,‘log‘);

logBW4=im2uint8(BW4)+J;

figure;

%imshow(BW4);

subplot(1,2,1);

imshow(J);

title(‘original image‘);

subplot(1,2,2);

imshow(logBW4);

title(‘Laplacian augmented image‘);

% canny

BW5=edge(I,‘canny‘);

cannyBW5=im2uint8(BW5)+J;

figure;

%imshow(BW5);

subplot(1,2,1);

imshow(J);

title(‘original image‘);

subplot(1,2,2);

imshow(cannyBW5);

title(‘Canny augmented image‘);

% gaussian & canny

% h=fspecial(‘gaussian‘,5);

% fI=imfilter(I,h,‘replicate‘);

% BW6=edge(fI,‘canny‘);

% figure;

% imshow(BW6);

figure;

subplot(2,3,1), imshow(BW1);

title(‘sobel edge detect‘);

subplot(2,3,2), imshow(BW2);

title(‘roberts edge detect‘);

subplot(2,3,3), imshow(BW3);

title(‘prewitt edge detect‘);

subplot(2,3,4), imshow(BW4);

title(‘log edge detect‘);

subplot(2,3,5), imshow(BW5);

title(‘canny edge detect‘);

% subplot(2,3,6), imshow(BW6);

% title(‘gasussian&cannyedge detect‘);

figure;

subplot(2,3,1), imshow(sobelBW1);

title(‘sobel edge detect‘);

subplot(2,3,2), imshow(robertBW2);

title(‘roberts edge detect‘);

subplot(2,3,3), imshow(prewittBW3);

title(‘prewitt edge detect‘);

subplot(2,3,4), imshow(logBW4);

title(‘laplacian edge detect‘);

subplot(2,3,5), imshow(cannyBW5);

title(‘canny edge detect‘);

下面的Matlab程序是精简的边缘提取实现：

clear;clc;

I=imread(‘lena.bmp‘);

I=rgb2gray(I);

imshow(I,[]);

title(‘Original Image‘);

sobelBW=edge(I,‘sobel‘);

figure;

imshow(sobelBW);

title(‘Sobel Edge‘);

robertsBW=edge(I,‘roberts‘);

figure;

imshow(robertsBW);

title(‘Roberts Edge‘);

prewittBW=edge(I,‘prewitt‘);

figure;

imshow(prewittBW);

title(‘Prewitt Edge‘);

logBW=edge(I,‘log‘);

figure;

imshow(logBW);

title(‘Laplasian of Gaussian Edge‘);

cannyBW=edge(I,‘canny‘);

figure;

imshow(cannyBW);

title(‘Canny Edge‘);

原文：http://www.cnblogs.com/AndyJee/p/3737325.html